Arguments
Bitcoin Node
Most of what people think about Bitcoin, nodes etc.
https://books.google.co.uk/books/about/Complex_Social_Networks.html?id=CEVSnW-cPnsC&source=kp_cover&redir_esc=y
The Kappa of Bitcoin connectivity is not what people see. Let use start with 6.1 on the topic of Gamma
https://www.cs.cornell.edu/~ie53/publications/btcProcFC.pdf
"Because selfish mining is reactive, and it springs into action only after the honest nodes have discovered a block X, it may seem to be at a disadvantage. But a savvy pool operator can perform a sybil attack on honest miners by adding a significant number of zero-power miners to the Bitcoin miner network. These virtual miners act as advance sensors by participating in data dissemination, but do not mine new blocks"
We call these nodes, they are wallets.
Gamma is set and modeled using using a low kappa Power Distribution network. Bitcoin is an extremely high kappa Poisson distributed network.
To see this:
Model the node connectivity.
- Use a Kamada-Kawai algorithm for the layout.
- Model distance and the spreading conditions
If you make the wrong assumption about a network, you get horribly wrong results. If you make the assumption that shares trade using a Gaussian distribution in place of a power law, then we see large hedge traders (Long Term Capital) get into trouble. The maths can be "good" but if it is the wrong maths modeling the wrong system, what does it matter?
https://arxiv.org/pdf/cond-mat/9903357.pdf
Key assumption 1 - Selfish Miners
"The virtual miners are managed by the pool, and once they hear of block X, they ignore it and start propagating block P. The random peer-to-peer structure of the Bitcoin overlay network will eventually propagate X to all miners, but the propagation of X under these conditions will be strictly slower than that of block P."
Here the addition of a small number of nodes we start to impact the network.
"By adding enough virtual nodes, the pool operator can thus increase γ".
What is enough?
In the SM Model, these are pool members that do not mine. They are a Babaioff et al (2012) Sybil.
Babaioff, M., Dobzinski, S., Oren, S., Zohar, A.: On Bitcoin and red balloons. In: ACM Conference on Electronic Commerce. pp. 56–73 (2012)
The Selfish Mining authors have used depth and gamma that is incorrect, but at least (on p 61) Babaioff et al (2012)
"There is no Sybil-proof reward scheme in which information propagation and no duplication are dominant strategy for all nodes at depth 3 or less." Babaioff et al (2012) have considered the effect of distinct depths in the system.
For some depths, the network was demonstrated to be Sybil proof. The statement is that "Notice that this scheme exhibits in equilibrium low overhead, Sybil proofness, and provides the nodes with an incentive to propagate information."
So, can be see that it is extremely important first of all to have a correct model of the network? Modeling the wrong network means little - this is a paper on the Bitcoin network, not a separate and distinct free scale network graph.
Questions to see if any of you know:
- What is the condition for "unbounded spread" in Bitcoin?
- How many Giant components does Bitcoin exhibit?
- How many edges / vertices are there in the Bitcoin network? Is this directed or undirected?
- What is the Eigenvector of the network and nodes?
These questions are critical, if you cannot answer these, you cannot start to understand the system in Bitcoin. Centrality is good in network propagation, it is not the same as centralisation. I suggest that people read up on this.
Now, what is the Normailised Closeness Centrality of Bitcoin?
Between-ness centrality?
Eigen Vector Centrality?
To work, the addition of these gamma altering Sibyls needs to alter Gamma.
We are adding nodes that in their introduction are acting in a manner analogous to the deletion of a random node. This is a consequence of vertices reconnecting to this new Sibyl node and redefining the network. Even in a low connectivity Barabási form network would we see a dramatic increase in mean-shortest path length (or a dramatic decrease in the clustering coefficient). It is rare for this and Bitcoin is far more robust than a Small world model.
This is one of the minor points that in itself invalidates the entirety of this (Selfish Miner) paper.
As you get each of these points, I will have you go deeper into the rabbit hole that is Bitcoin and you can learn why this for of attack is not feasible.
What is the effect of changing from a Poisson to a Power law network? What is the distance and how does this change centrality measurements?**
In Babaioff (2012) what was the study of Gamma referring to?
How were these findings used in the Selfish Miner paper?
If Bitcoin was degraded to a Small World system, what would change?
Babaioff, M., Dobzinski, S., Oren, S., Zohar, A.: On Bitcoin and red balloons. In: ACM Conference on Electronic Commerce. pp. 56–73 (2012)
If you cannot answer those questions, you cannot even start to answer the assumptions used in SM. Let's think on Percolation theory... It the propagation of blocks and Transactions Subcritical or supercritical or something in between?
What is the Sharp threshold for Bitcoin's Percolation model?
Smirnov, Stanislav (2001). "Critical percolation in the plane: conformal invariance, Cardy's formula, scaling limits". Comptes Rendus de l'Académie des Sciences - Series I - Mathematics. 333 (3): 239–244.
Next, to go back to why this matters...
The first transaction released is on an open network with large inter-connectivity. It is an SEIR-C model and SIR as a simplification. The nodes that have received a block are not. Once you have recieved a TX, that node is now immunised from a competing block.
Node response:
1 Receive a valid TX or Block
2 Reject an equal but competing block that comes even a second later
As the nodes reject the new block, they do not forward it
This means that the distance and centrality values for the first node to release are NOT the same as the later ones.
You cannot model the transmission using the same formula and data... Bad assumptions lead to bad models. It is simpler, but wrong. As the SM reacts, they are on the "pruned" network graph. The nodes the SM can send to are the ones who have not received the initial release of the TX or Block. So, you cannot use the same probability for each. Conditional probability needs to incorporate the Bayesian prior.
Oh and it seems to work, but in the same way that a Martingale strategy does,
https://www.forebet.com/en/betting-systems/88-the-martingale-fallacy
https://en.wikipedia.org/wiki/Martingale_(betting_system).
SM is a poor Martingale, SM is known as a limited response system anti-martingale. The SM network is an overlay power law distribution. The SM would need to have at least 50 % to be the giant network.
"In the first scenario where the honest nodes succeed in finding a block on the public branch, nullifying the selfish pool’s lead, the pool immediately publishes its private branch (of length 1). This yields a toss-up where either branch may win."
But, its not a toss up. It is not instant. The Selfish miner needs to wait and validate a block from the Honest Miners. The Selfish miner has a response that is conditional to seeing the block. And they assume the same node connectivity, not seeming that the release of the block from the Honest nodes starts to inoculate the system against a second block (no time stamps). They also need to ensure that no pool member defects. A pool member finding a block needs to be paid.
So, they are "in" on this or they are not and want money now... The simple matter is that I have linked all you need to know to understand the problem. If you don't believe it or don't get it, I don't have the time to try to convince you.
That is the best I can offer sorry. Yes, there is no detail of the model. They use Babaioff, M., Dobzinski, S., Oren, S., Zohar, A.: On Bitcoin and red balloons. In: ACM Conference on Electronic Commerce. pp. 56–73 (2012) and yet fail to set the parameters
And it this is simple, you need to state the topology. The maths for each varies. No, you do not get to say what the system is and assume. Sorry, but science does not work this way.
Case 1: Selfish miner (SM)
You return a part of the reward.
The hidden block is at risk.
The strategy is a Martingale. The gamblers fallacy in that you mine a block with a part probability of gaining a second.
They forget that quickly broadcasting this block gains a near 100% chance of it being accepted. However, hiding it means that they compete after the fact. You go from 100% to a fraction of the discovered block.
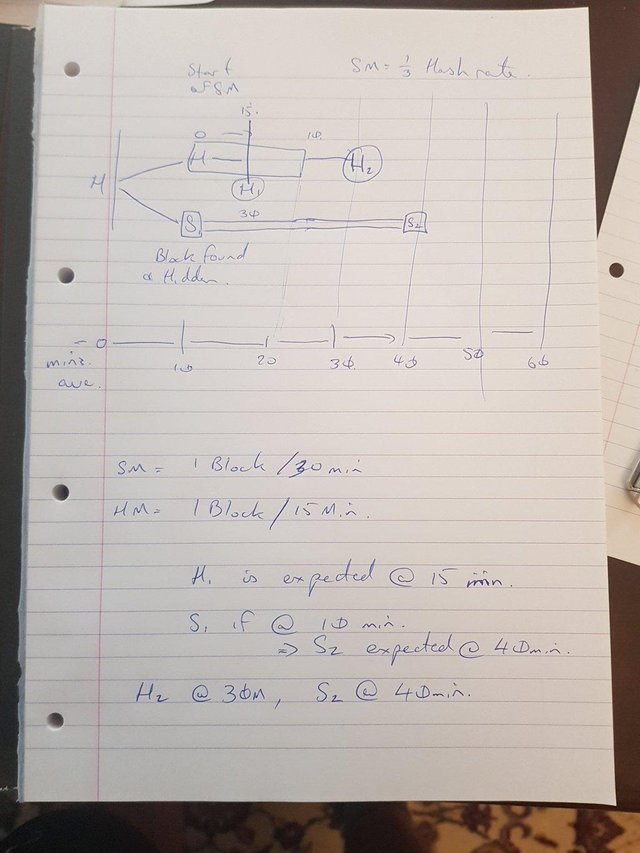
Case 2: No SM
You (nearly) always gain a 100% reward of the first block mined and released.
IF SM releases on the 15 min point where H1 is expected, they have a fractional chance of a reward. This at Gamma 0 is 2/3.
If SM releases as they discover the block, they have a near 100% of the reward.
They forget that ALL miners working on their block is better. They have a state diagram that solves every 10 mins on both HM and SM. This is wrong, the difficulty changes only each 2016. That was accounted into the original design. The state diagrams only make sense for 2x 50% miners. The state diagrams need to have an expected time for a 1/3rd miner to solve at 30mins a block and a 2/3rd miner at 15 mins. Together these creates a 10 min average.
The system is memoryless. It is like black and red on a roulettle table, 100 reds in a row has no effect on the next red. The model in the paper is wrong. They treat this as lossless. They have the SM lose a block and ignore this. They send After the HM and hence 2/3 of the time in their graph model (99.8% on the real version of Bitcoin network) the SM loses and gets. Bitcoin Blocks are not timestampted, first recieved, first mined on. Next and this is what that diagram relates to...
"The protocol will adapt the mining difficulty such that the mining rate at the main chain becomes one block per 10 minutes on average." [2]
Flawed assumption and flawed model.
The state diagram adjusts the main chain to run at 10 mins. The truth is that this is lower. The Honest miners (HM) at a 2/3rd ratio mine at 15 mins (10/[1-(2/3)]) and the Selfish miner at 30 mins (10/[1-(1/3)]) creating more orphans and making the chain take longer until the difficulty adjusts.
The protocol adjusts over 2,016 blocks. This means, that for the numbers of blocks used in the SM paper, the protocol does not adjust [1].
[1] https://en.bitcoin.it/wiki/Difficulty
[2] https://www.cs.cornell.edu/~ie53/publications/btcProcFC.pdf - Page 11 (S 4.2)
The result is that the state diagrams are wrong other than for a selfish miner with > 50% of the hash rate (and they do not need to selfish mine).
Gamma can never be as large as they state. This comes both from the network (that has it close to zero in any case) and simple maths.
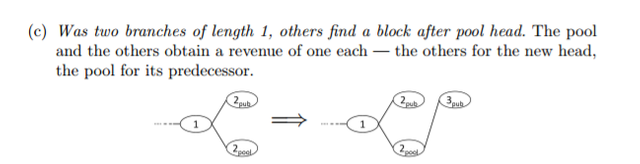
If a HM from the 2/3rd of all Honest miners has a pool of 1/3rd of the total power, they will always have 1/3rd of the blocks they mine and will not drop these for the SM ones. So, there is no case where this can be a gamma of 1 in any case, but the distribution is wrong in any event. That leads to the next point...

Equations (6) and (7) are the wrong equations. It does not matter that the maths is fine using these, as they are not the correct formula for conditional probability. This being defined as the probability of an event ( A ), given that another ( B ) has already occurred.
As we have the SM only reacting after the release of a block and this being seen by the HM, this becomes the probability of an event (SM releasing), given that another (HM mining a block) event has already occurred.
Equations (6) and (7) are:
[1] https://www.cs.cornell.edu/~ie53/publications/btcProcFC.pdf - Page 11 (S 4.2)
That equation has assumed Statistical independence. This is not the case as they cannot send to 100% of nodes and replace those from the Honest miners. Remember, honest miners will not replace a block for a single block held by the Honest miner already.
So, we have a dependent condition and need to use P(SM | HM). It cannot be assumed that P(A|B) ≈ P(B|A).
This is a common fallacy. It even has a name. Not taking the prior probability into consideration and not negating this from the equation (in part or completely) is refered to as base rate neglect. In this series of equations, we have both that and the reverse, insufficient adjustment from the prior probability, a fallacy known as statistical conservatism.
This is covered in detail as a fallacy here:
http://lesswrong.com/r/discussion/lw/9om/the_conditional_fallacy_in_contemporary_philosophy/
See Kolmogorov, Andrey (1933). Grundbegriffe der Wahrscheinlichkeitsrechnung (in German). Berlin: Julius Springer.
W. Feller, "An introduction to probability theory and its applications," 1957.Page 116 - (1.4)
**Conclusion: **
The Selfish miner paper forgot to subtract the intersection probability.
Wrong formula.
Incorrect model
Wrong assumptions.
Extra
https://steemit.com/bitcoin/@zillionaire/sefish-mining-fallacy-part-3-stochastic-modelling
Full index of Selfish Mining Series
https://steemit.com/bitcoin/@zillionaire/sefish-mining-fallacy-index-updating
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit