[2022/09/08 복습] 헷갈리는 자료구조론 - 그래프, 정렬

• 전날 공부량: 100문제

• 헷갈리는 자료구조론: 그래프, 정렬

1. 이분할 그래프
   
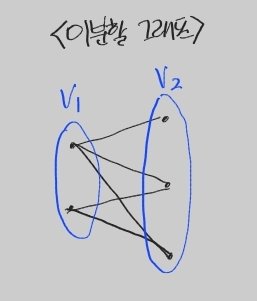
   ▶정점을 서로소인 집합 V1과 V2로 나눌 때, V1의 정점과 V2의 정점을 잇는 간선만 존재하고 V1내의 정점들 또는 V2내의 정점들을 잇는 간선이 존재하지 않는 그래프
   ▶최대 간선 수: m*n (m: V1의 노드 수, n: V2의 노드 수)

1. 그래프 관련 용어
   ▶ 차수: 한 정점에 부속된 간선 수
   ▶ 진입차수: 방향 그래프에서 정점 V가 Head가 되는 간선 수
   ▶ 진출차수: 방향 그래프에서 정점V가 Tail이 되는 간선 수
   차수: 진입차수 + 진출차수
   
   ▶ 오일러 경로: 그래프의 모든 연결선을 꼭 한 번씩만 지나는 경로. 조건은 홀수점의 개수가 0개 또는 2개.
   ▶ 오일러 회로(사이클): 시작점과 종점이 같은 오일러 경로
   ▶해밀턴 경로: 모든 점을 꼭 한 번씩만 지나면서 시작점으로 돌아오지 않는 경로. NP-COMPLETE 문제
   ▶해밀턴 회로: 시작점과 종점이 같은 해밀턴 경로
   
   cf) NP-COMPLETE 문제: Clique Optimization Problem, Satisfiability, Travelling salesperson Decision Problem, 오일러 회로, 해밀턴 경로 등

2. 그래프의 표현: 인접행렬
   ▶ 무방향 그래프: 정점 i의 차수 = 그 행의 합
   ▶ 방향 그래프: 행의 합 = 진출차수, 열의 합: 진입 차수
   전체 차수= 진입차수 + 진출차수
   ▶ 시간복잡도
   간선의 존재 여부: O(1)
   정점의 차수: O(n)
   간선 수: O(n²)

3. 그래프의 표현: 인접리스트
   ▶ 무방향 그래프의 각 정점의 차수 = 그 정점에 대한 인접 리스트에 속한 노드 수
   ▶정점 n개, 간선 e개인 경우,
   무방향 그래프를 인접리스트로 표현: n개 헤드 노드, 2e개의 리스트 노드(연결리스트)
   방향 그래프를 인접리스트로 표현: n개 헤드 노드, e개의 리스트 노드 필요
   ▶ 그래프 G 간선 수: O(n + e)

4. 최소 비용 신장트리
   ▶ Greedy Method(갈망법, 욕심쟁이 방법): Kruskal, Prim 알고리즘, Sollin 알고리즘 등.
   위상정렬, Huffman code tree에도 갈망법 적용 가능. 광범위한 프로그래밍 문제에 적용 가능.
   각 단계에서 내려진 결정은 번복이 불가능. 결정이 가능한 해를 도출해 낼 수 있는지 확인해야 함.
   ▶Kruskal 알고리즘
   (1) 비용이 적은 간선부터 선택
   (2) 사이클 생성되지 않도록
   (3) 간선 수가 n-1개가 되면 중단
   ▶Prim 알고리즘
   하나의 시작 정점으로부터 인접한 간선들 중 최소 비용을 갖는 간선 선택

5. 최단 경로
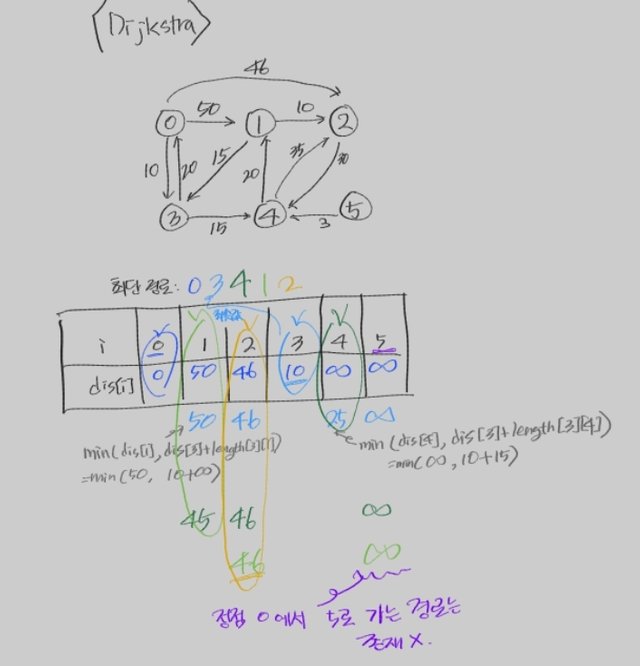
   ▶ Dijkstra(다익스트라) 알고리즘
   

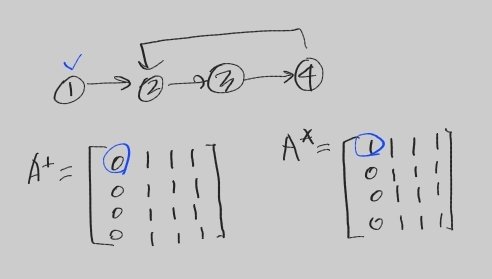
6. 이행적 폐쇄 행렬(A⁺)
   가중치 없는 방향 그래프 G의 모든 i, j의 정점에서 i -> j의 경로가 존재하면 1, 없으면 0이 된다.
   패스가 0인 경우는 포함하지 않는다.

7. 반사 이행적 폐쇄 행렬(A^*)
   방향 그래프 G에서 i -> j로의 경로의 길이가 0이거나 0보다 크면 1, 없으면 0이 된다.
   자기 자신 모두 1(패스가 0인 경우를 포함)
   

8. 정점작업 네트워크(AOV Network)
   ▶위상정렬(Topological sort):
   (1) 선행자가 없는 정점들 정렬
   (2) 이 정점들과 이들로부터 나오는 모든 간선들 삭제
   (3) 모든 정점들이 정렬됐거나, 남아있는 정점들이 모두 선행자를 가지고 있어 어떤 정점도 제거할 수 없을 때까지 이 두 단계 반복
   ▶ 모든 정점들이 선행자를 가진다는 것은 그 네트워크에 사이클이 있는 경우임. 이때는 위상 순서를 결정할 수 없기 때문에 그 프로젝트는 수행이 불가능한 상태로 결정
   ▶ 큐, 스택 사용

9. 간선작업 네트워크(AOE Netowork)
   ▶ 임계경로(critical path)
   프로젝트를 완료하는 최소 시간.
   최장 경로의 길이

10. 정렬
    ▶실행시간
    

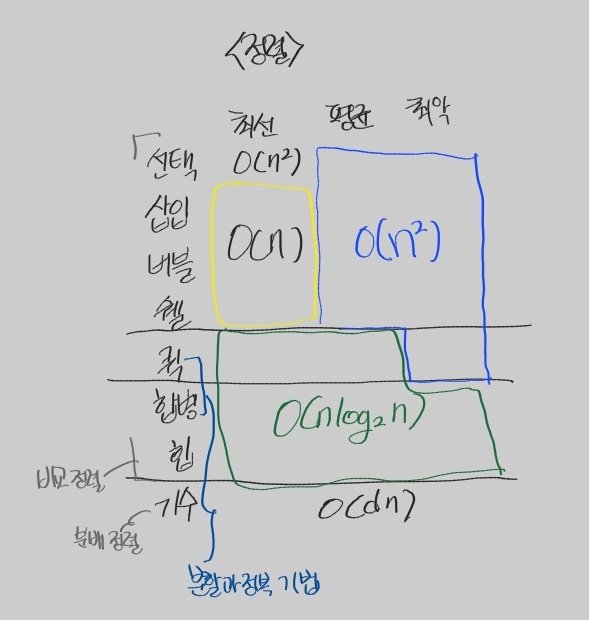
11. 선택 정렬
    ▶ 최솟값 또는 최댓값을 선택하여 리스트의 처음이나 마지막으로 이동.
    ▶ 총 비교 횟수: n(n-1)/2

12. 거품 정렬
    최대 비교 횟수: n(n-1)/2
    평균 비교 횟수: n(n-1)/4
    최소 비교 횟수(flag 사용 시): n - 1

13. 삽입 정렬
    
    ▶ 이미 정렬된 레코드에 정렬되어 있지 않는 레코드를 삽입시켜서 재정렬
    ▶ 최대 비교 횟수: n(n-1)/2
    평균 비교 횟수: n(n-1)/4
    최소 비교 횟수: n - 1

14. 쉘 정렬
    
    ▶ 자료를 매개변수(d)의 값에 따라 여러 부분으로 나눠 각 부분을 삽입정렬 방식으로 정렬.
    ▶ 상위의 값과 하위의 값을 간격 d를 기준으로 interchange
    ▶ 최대 비교 횟수: n(n-1)/2
    평균 비교 횟수: n(n-1)/4
    최소 비교 횟수: n - 1

매일 하려 했는데 그게 잘 안되네요.
200문제 좀 풀어보즈아..!!
오늘도 화팅~

Posted through the AVLE Dapp (https://avle.io)