
The general form of wave function
Lets consider a simple the case of one-dimensional motion of a particle of mass m and potential energy V(x).
The space part 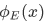 of the wave function of a stationary state with energy E satisfies the time-independent Schrodinger equation:
of the wave function of a stationary state with energy E satisfies the time-independent Schrodinger equation:
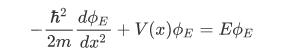
that is
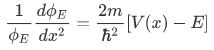
Case 1 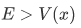
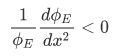
Case 2 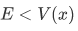
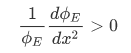
These features of 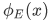 are more clear in the following figure:
are more clear in the following figure:
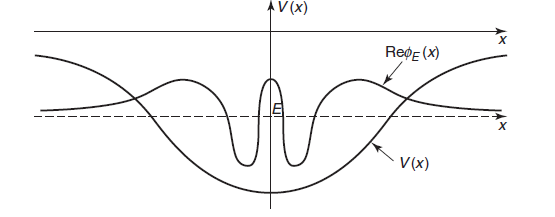
in which we plot the real part of 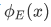 at the level of E.
at the level of E.
Remarks:
- the kinetic energy is greatest at the deepest part of the well (centre in this case), that is, k is largest, and hence the local wavelength
 is shortest, near the centre of the well.
is shortest, near the centre of the well.
Similarly, a higher E correspond to higher values of the kinetic energy T at all points, this implies that the wave functions have more oscillations and hence more nodes.
Now, consider a potential energy that is piecewise-constant in space, as in the case of "potential barrier" shown below,
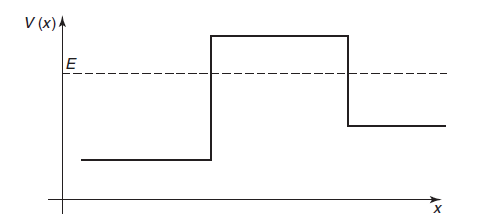
In regions in which V is constant and smaller than E, a region often referred to as classically allowed regions such as the regions to the left and to the right of the barrier, the space-dependent part of the wave function always has the oscillatory form:
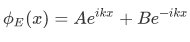
where k is found from the relation:
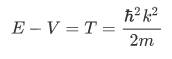
in which V is the constant potential energy in the given region. Thus the wave number is given by
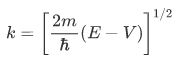
In the regions in which V is constant and greater than E (classically forbidden regions, such as the region of the barrier), the space-dependent part of the wave function has the general form of an exponentially increasing and an exponentially decreasing term:
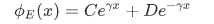
where V is the constant potential energy in the given regions. Thus, $\gamma$ is given by
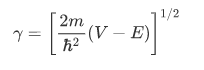
One might wonder how to proceed with the space-dependent wavefunction we have without knowing the values of the coefficients, A,B or C,D. To find the values of these coefficients, we have to impose the following requirements on the wave function
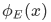 in all regions of constant V,
in all regions of constant V,
- the wavefunction
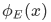 is continuous
is continuous - the first derivative
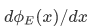 is continuous [except at singularities or infinite discontinuities of V(x)
is continuous [except at singularities or infinite discontinuities of V(x) - the function
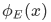 is normalized
is normalized
These conditions are, in fact, general physical requirements on the space part of the wave function of a particle with a definite energy E.
In turns out, that some arbitrary values of E does not satisfy these conditions, and that time-independent Schrodinger equation has solutions that satisfy these requirements only if the energy E is specified to have a value belonging to a specified spectrum.
In certain regions of energy, this spectrum may be discrete and so the above requirements lead naturally to energy quantization.
You got a 6.36% upvote from @minnowvotes courtesy of @pauldirac!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
You got a 18.14% upvote from @joeparys! Thank you for your support of our services. To continue your support, please follow and delegate Steem power to @joeparys for daily steem and steem dollar payouts!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit