
Canvas source Explain any two variables and expressions types other than that which are explained in this course.(Practical and algebric examples are required!) |
|---|
Variables
A variable is like a mystery box—you don’t know what’s inside, but it can hold any number. In algebra, we usually use letters like x, y, or z as variables. For example, in 2x + 3, the ‘x’ is the variable because its value can change. Think of it like a cookie jar; the number of cookies inside depends on how many you eat—or how many you sneak at midnight!
Expressions
Expressions are like recipes where numbers, variables, and math operations (like +, -, ×) come together. Take 2x + 5: here, 2x means "twice whatever’s in the mystery box," and 5 is the constant. It’s like baking cookies: 2x is the dough you shape, and 5 is the chocolate chips—no matter what, they always stay the same.
Real-Life Twist
Variables and expressions are all around us. Imagine you’re earning $15 an hour. If ‘x’ is the number of hours you work, then 15x tells you how much you’ll earn. The more you work, the bigger the paycheck—unless you’re distracted by snacks.
Algebra may sound scary, but it’s super useful. Whether you’re calculating distance, saving money, or even estimating how many pizzas to order for a party, variables and expressions save the day—like superheroes in math!
Variables and expressions are critical elements in solving problems in algebra and relating values with one another. Variables represent unknown or changing values, and an expression is the combination of variables, constants, and mathematical operations. Both come in different types that serve various purposes in mathematical calculations and practical life. Let's proceed with the types of variables and expressions.
Types of Variables
Independent Variable: An independent variable is a value that is not affected by other variables in the equation. It stands on its own. For example, in the equation y = 2x + 3, the variable ‘x’ is independent because its value can be chosen freely, and it determines the outcome of ‘y’. Think of it like exercise duration—you decide how long to work out!
Dependent Variable: A dependent variable relies on the independent variable. It changes based on the value of another variable. In the equation y = 2x + 3, ‘y’ is the dependent variable because its value depends on ‘x’. For instance, the more you exercise (x), the more calories you burn (y).
Types of Expressions
Numerical Expressions: These consist of only numbers and mathematical operations like addition, subtraction, multiplication, and division. For example, 2 + 3 × 5 is a numerical expression. It doesn’t involve variables—just plain numbers and calculations, like figuring out the total cost of snacks you bought.
Algebraic Expressions: These include variables, constants, and mathematical operations. For example, 3x + 7 is an algebraic expression where 3x involves a variable ‘x’, and 7 is a constant. It’s like calculating the cost of multiple items when the price per item changes (x being the price).
By understanding these types, you can solve real-world problems with ease, from budgeting to tracking time and distance.
Show your way of evaluating of an algebraic expression if values of variables are given? Step by step explanation required |
|---|
When you’re given an algebraic expression and a set of values for its variables, the goal is to find the value of the expression by substituting those values in and simplifying the expression. Evaluating expressions is an essential skill in algebra because it helps you understand how variables work in real-life scenarios.
Whether you're calculating costs, distances, or even how much ice cream you’ll get from the store (depending on how much money you have!), algebra helps you solve those everyday puzzles.
Let's break it down and have some fun with this process!
Step 1: Write Down the Given Expression
This is the first step, and it’s as simple as it sounds: write down the expression clearly. An algebraic expression typically consists of numbers, variables, and mathematical operations. The variables (often represented by letters like x, y, or z) are placeholders for unknown values that can change.
Example Expression:
Let’s work with the following expression:
2x + 3y - 4z
In this expression, we have three variables: x, y, and z. The numbers in front of each variable (like 2, 3, and -4) are called coefficients, and they tell us how much to multiply each variable by. The plus and minus signs are mathematical operations, which tell us whether to add or subtract the results.
Given Values:
- x = 5
- y = 2
- z = 3
At this point, we just write the expression down and prepare for the next step.
Step 2: Substitute the Given Values
Now that we have the values for the variables, it’s time to substitute them into the expression. Think of substitution as filling in the blanks. You’re replacing the variables with their actual values to see what the expression equals.
Expression Before Substitution:
2x + 3y - 4z
Values to Substitute:
- x = 5
- y = 2
- z = 3
After substituting, the expression looks like this:
2(5) + 3(2) - 4(3)
Notice how the variables x, y, and z have been replaced with their values. Now, you have an expression full of numbers, ready to be simplified!
Step 3: Perform Multiplication First
According to the Order of Operations, we must handle multiplication (and division) before addition and subtraction. This rule helps avoid confusion, as expressions with multiple operations can be interpreted differently if the order isn’t followed.
So now we’ll multiply the numbers in each part of the expression:
- 2 × 5 = 10
- 3 × 2 = 6
- 4 × 3 = 12
After multiplying, the expression now looks like:
10 + 6 - 12
This step is crucial because it ensures that the values of the variables are accounted for correctly before moving on to the next operations.
Step 4: Perform Addition and Subtraction
Once we’ve handled the multiplication, the next step is to add and subtract the results. You do this from left to right, just like reading a sentence from start to finish. This step is all about simplifying the expression by combining the numbers.
Expression After Multiplication:
10 + 6 - 12
Now, we follow the left-to-right rule:
- First, 10 + 6 = 16
- Then, 16 - 12 = 4
So, after adding and subtracting, the final simplified expression is:
4
Step 5: State the Final Answer
At this point, we’ve completed all the necessary operations to simplify the expression. The value of the expression is the final result after substituting the values and performing the operations. This is the value we were looking for!
Final Answer:
The value of the expression 2x + 3y - 4z when x = 5, y = 2, and z = 3 is:
4
This is your final answer—yay, you solved the puzzle!
A Fun Example: Let's Multiply with a Twist!
Imagine this: You’re buying ice cream cones, and each cone costs $3. But if you buy more than two cones, you get an extra topping that costs $2. If x represents the number of cones, how much will you pay if you buy x = 4 cones?
Here’s the expression:
3x + 2 (for the topping).
Substitute x = 4:
3(4) + 2 = 12 + 2 = 14
You’ll pay $14 for the 4 ice cream cones and the topping. Algebra makes even ice cream decisions fun and easy!
Simplify this expression: 3(2x - 1) + 2(x + 4) - 5 |
|---|
 |
|---|
We’ll simplify this expression by first distributing and then combining like terms.
Step 1: Distribute the numbers into parentheses.
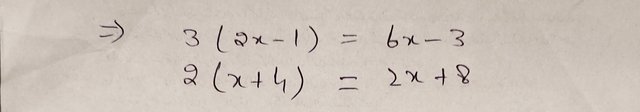 |
|---|
Distribute 3 to (2x - 1) and distribute 2 to (x + 4).
So, the expression becomes:
 |
|---|
- 6x−3+2x+8−5
Step 2: Combine like terms.
Now, combine the terms with x and the constants.
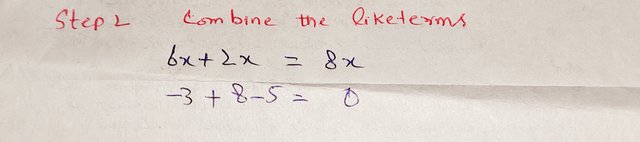 |
|---|
So, the simplified expression is:
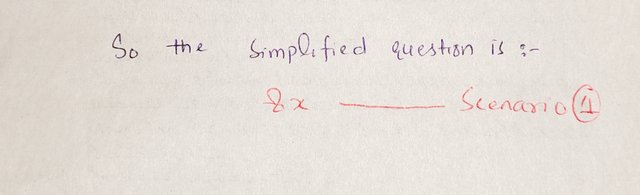 |
|---|
Evaluate this expression: (x^2 + 2x - 3) / (x + 1) when x = 2 |
|---|
 |
|---|
Step 1: Substitute x = 2 into the expression.
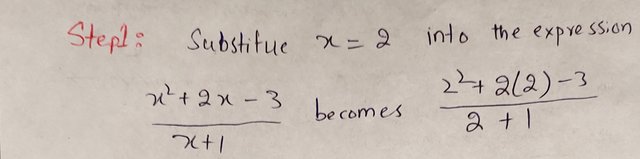 |
|---|
Step 2: Simplify the numerator and denominator.
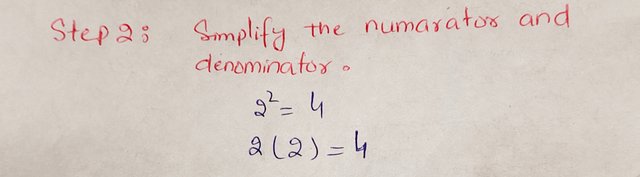 |
|---|
So, the numerator is:
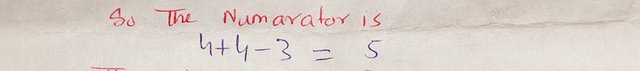 |
|---|
The denominator is:
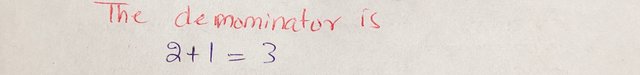 |
|---|
Step 3: Simplify the final expression.
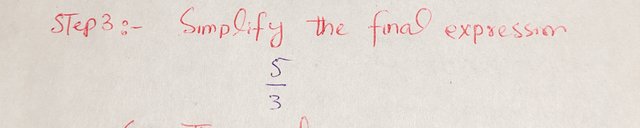 |
|---|
So, the value of the expression when x = 2 is:
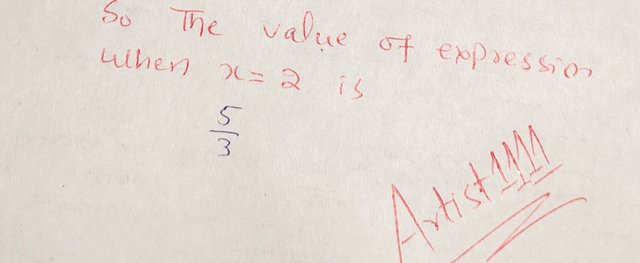 |
|---|
Simplify this expression: 3(2x - 1) + 2(x + 4) - 5 |
|---|
 Final part Final part |
|---|
We’ll solve this equation step by step.
Step 1: Expand both sides of the equation.
Distribute the 3 on the right side of the equation:
 |
|---|
Simplify the right side:
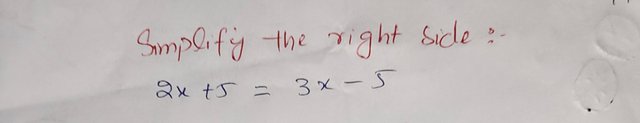 |
|---|
Step 2: Move all terms involving x to one side of the equation.
Subtract 2x from both sides:
 |
|---|
Step 3: Solve for x.
Add 5 to both sides:
So, the solution to the equation is:
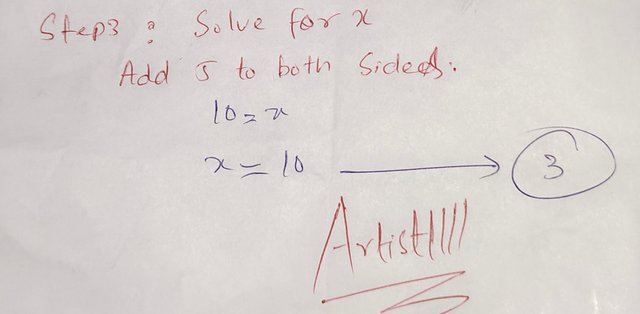 |
|---|
Final Answers:
- Simplified expression: ( 8x )
- Evaluated expression: (5/3)
- Solution to the equation: (10)
These steps should help you understand how to approach simplifying expressions, evaluating expressions, and solving equations!
Task 4 : Theory Behind Algebraic Expressions and Profit Calculations |
|---|
Theory Behind Algebraic Expressions and Profit Calculations
Algebraic expressions are mathematical statements that combine variables, constants, and operations. These expressions are commonly used to model real-world situations, making them an essential tool in problem-solving across various fields like economics, business, and engineering.
1. Bakery’s Daily Profit Expression
In this case, we’re dealing with a profit calculation for a bakery selling two types of bread: whole wheat and white bread. The goal is to create an expression that represents the total daily profit of the bakery. Let’s break down the steps involved:
Step 1: Defining the Variables
We use x to represent the number of white bread loaves sold by the bakery. Since the total number of loaves sold per day is fixed at 250, the number of whole wheat loaves sold will be 30 more than the number of white bread loaves. This gives us the expression for whole wheat loaves sold as x + 30.
So, we now have:
- x = number of white bread loaves sold
- x + 30 = number of whole wheat loaves sold
Step 2: Profit per Loaf
Each type of bread has its own profit associated with it:
- The bakery earns $0.50 for each white bread loaf sold.
- The bakery earns $0.75 for each whole wheat loaf sold.
Step 3: Writing the Profit Expressions
To calculate the total profit, we need to multiply the number of loaves sold by the profit per loaf for each type of bread:
- Profit from white bread loaves: 0.50 × X
- Profit from whole wheat loaves: 0.75 × ( X + 30)
Step 4: Total Profit Expression
The total profit is simply the sum of the two individual profits:
Total Profit=(0.50×x)+(0.75×(x+30))
This is the algebraic expression representing the bakery’s total daily profit.
Step 5: Substituting the Value of x
To find the actual total profit for a specific number of loaves, we substitute the value of x into the expression. If x = 110 (meaning 110 white bread loaves are sold), the expression becomes:
Total Profit=0.50×110+0.75×(110+30)
Now we calculate:
Total Profit=55+0.75×140=55+105=160
So, the total daily profit is $160 when 110 white bread loaves are sold.
2. Car Rental Cost Expression
In the case of the car rental, we are given a scenario where the rental cost depends on the number of hours the car is rented. The expression changes based on whether the rental period is less than or equal to 4 hours or greater than 4 hours. This type of problem involves creating piecewise functions—expressions that define different formulas for different conditions.
Step 1: Rental Cost for 4 Hours or Less (x ≤ 4)
When the rental period is x hours (where x ≤ 4), the cost is described by the expression 2x + 15. Here:
- 2x represents the cost per hour, where the car is charged $2 per hour.
- 15 represents a fixed additional charge, possibly for basic insurance or handling.
This gives us the first formula:
- Total Cost=2x+15
Step 2: Rental Cost for More than 4 Hours (x > 4)
If the car is rented for more than 4 hours, the rental company offers a special package deal. The cost for this package is represented by the expression 3x - 2. Here:
- 3x represents the charge for the rental, where the price is $3 per hour for rental periods over 4 hours.
- -2 represents a discount of $2 offered for rentals longer than 4 hours.
This gives us the second formula:
- Total Cost=3x−2
Step 3: Putting the Two Expressions Together
We now have two separate expressions based on the value of x (the number of hours the car is rented):
- If x ≤ 4, the cost is:
- Total Cost=2x+15
- If x > 4, the cost is:
- Total Cost=3x−2
These two expressions together form a piecewise function, which tells us how the total cost varies depending on the number of rental hours.
Step 4: Simplifying the Expressions
Both expressions, 2x + 15 and 3x - 2, are already in their simplest forms. There’s no further simplification needed. However, we can clearly see that:
- For x ≤ 4, the cost increases linearly with the number of hours rented.
- For x > 4, the cost increases at a higher rate, but with a discount for longer rentals.
Conclusion
In both of these problems, we’ve used algebraic expressions to model real-world scenarios—calculating profit for the bakery and rental cost for the car. Algebra is a powerful tool because it allows us to represent relationships between different quantities and calculate outcomes based on those relationships.
For the bakery’s profit, we wrote an expression for the total profit based on the number of loaves sold and the profit per loaf. By substituting a specific value for the number of white bread loaves sold, we calculated the total profit.
For the car rental cost, we used a piecewise function to represent the rental cost based on the number of hours rented, taking into account different pricing schemes for different rental periods.
By breaking down the problems step by step, we ensure accuracy and make sure we understand the process behind creating and simplifying algebraic expressions in practical scenarios.
kind Regards
@artist1111

Adieu, folks!
May the winds of fortune
carry you to greatness!
May the winds of fortune
carry you to greatness!