
Hello friends and welcome to my article in the SLC: S22/W1 and I duly appreciate @khursheedanwar for the graceful thought of incorporate logic arithemtic into this great lessons. I love arithemtic and remain more than ready to share my thoughts on this great conquest.
Continuous Variables:
These can also be known as quantitative variables, they are specially used in groups observation, dividing data into indistinct groups and categories, which lack countable values. Examples; gender, marital status
link🔗
Continuous Variables:
Continuous Variables are quantitative variables that take number of valued within a range. The variables are measured along a continuum, representing very precise measurement. Good example is height, temperature, time.
An algebraic expression can be evaluated easily in simple ways. I would be showing guides on how to evaluate an algebraic expression. But firstly a background note must be made on algebraic expression.
Algebraic expression must eventually involve a variable, constant and one or more mathematical expressions. Importantly, it mustn't be equated to another value. Once an expression gets equated through an = it turns from an expression to an equation
Example: 50x + 45 - 20x is an algebraic expression due to the fact that it contains variables x special constants 50, 45 and 20. Mathematical operation which are + and - respectively.
Example of an algebraic equation would be 50x + 45 = 30 - 4x Once there is an = sign which comes to play it turns to an equation. From this the variables are xcoefficients are 50, 45, 30 and 4 respectively, mathematical operations + - =
Evaluating an algebraic expression would require using the PEMDAS expression technique which explains the basic approach. PEMDAS according to the lesson means Parentheses, Exponents, Multiplication, Division , Addition and Subtraction respectively As shared in the class
Lets imagine an algebraic operation
42 + 8 - 2 ÷(2×4)(5-3)
We firstly analyse the expressions in the parenthesis following the lesson guide, (2×4)=8 for first parenthesis and (5-3)=2
We multiply (8)(2) which gives us 16 We go further to analyze the other figures which are 42 + 8 -2 which gives 50-2 which is 48 We further divide 48÷16=3 therefore our final answer is 3
Simplify this expression: 3(2x - 1) + 2(x + 4) - 5
Evaluate this expression: (x^2 + 2x - 3) / (x + 1) when x = 2
Solve the following equation: 2x + 5 = 3(x - 2) + 1
 | 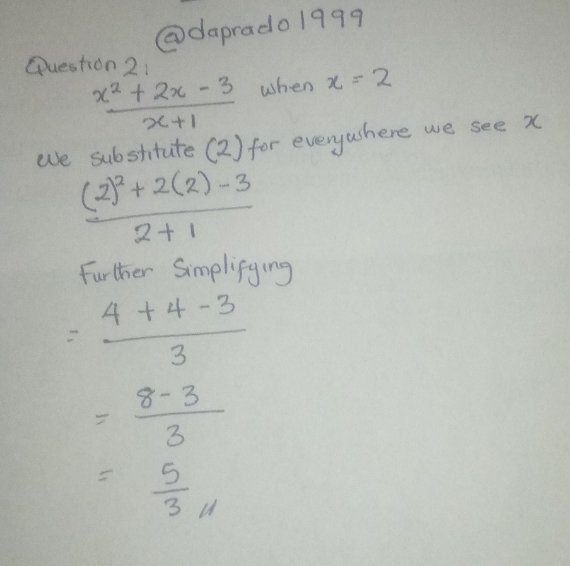 |
|---|
Solving the equation respectively in the screenshot below.
 |  |
|---|
We firstly define our parameters accordingly;
x represent assumed white bread loaf
30x represent assumed number of wheat
Therefore x+30x = 250
Simplifying for x we have...
31x = 250
Dividing both expressions by 31 to make x the subject we have;
x = 8.06
To check if we are correct we substitute 8.06 into the equation.
x+30x = 250
Substituting we have
8.06 + 30(8.06) = 250
8.06 + 241.8 = 249.86 approximately 250!
Profit margin determination is this;
0.50x + 0.75(x+30)
0.50(8.06) + 0.75(8.06+30) simplifying
4 + 38.81
Profit daily = $42.81
Scenario 2;
Total Cost = (2x +15)
Mentioned package = (3x-2)
number of hours = x
exceeded number of hours = 4+x
(2x+15)+(3x-2)=4+x
Simplifying
(2x + 15)+(3x-2)=4+x
2x+3x+15-2=4+x
5x-x= 4-15+2-3
4x= 12
Dividing both sides by 4
x= 3 hours
This is the mathematical representation of the word problem given and thus an algebraic expression for the tasked asked above.