| Design by canva app |
|---|

| Assalam-O-Alaikum Friends ♥️ |
|---|
| Welcome on my post ♥️! |
|---|
How are you? I hope you are all well. Today I am participating in a very interesting contest. It is organized by Professor @khursheedanwar. I am very happy to participate in this contest. And INSHALLAH we will learn a lot from your courses.

| Variables |
|---|
From the course I understand the concept of variables. Variables are alphabetically letters i.e (x , y and z) and their representation of value can changed and modified.
Let's suppose:
= 4x + 5y
x and y are variables.
| Types of variables |
|---|
- Discrete variables
- Continuous variables

| Discrete Variable |
|---|
Discrete variables are the type of variables that can takes a specific value in the range.
In other words, they don't have an infinite number of values.
For Example: If you count a set of items, then it's a discrete variables.
Number Of participants in this contest.
Number of items purchased from store.
Range of specified numbers is complete.

| Continuous Variable |
|---|
Continuous variables are the type of variables that has an infinite number of possible values. A continuous variable is the opposite of discrete variable.
For example, let's look at a person's age, weight and height. So if we want to know the age of a particular person then it comes in continuous variable.
The age of person (male or female) is 25.4 years.
If the weight of person consider 70.230kg then it is continuous variable.
The height of person is 6.1f.
Range of specified numbers is incomplete, i.e. infinite.

| Expression: |
|---|
From the course I clearly understand the concept of expression. Expression is the group of variables, constant and mathematical operation which combine together.
| Let's suppose! |
|---|
If I write an expression
8x + y = 4
In above equation there are three terms i-e 8x, y and 4.
x and y are variables.
4 is constant that can't changed.
8 is co-efficient of variable x.

| Types of Expression! |
|---|
Linear Expression
Rational Expression
| Linear Expression | Rational Expression |
|---|
| The highest power of the variables is one (1) is called linear expression as well as also called one degree equation. | The quotient p / q of two polynomials p (x) and q (y), where the denominator q is non zero is call rational expression. |
|---|
| From example we can understand the concept of Linear expressions. | From example we can understand the concept of Rational expressions. |
|---|
| We have expression 8x + y = 4 | Rational expression 2x^2yz / 2xyz |
|---|
| 8x + y = 4 | 2x^2yz / 2xy^2z |
|---|
| From above expression the power of x is one (1) and also power of y is one (1). So we understand the highest power of variables is one (1). | From above equation we can cut the same variables and constant. So one time 2, two times x, one time y and one time z in nominater and one time 2, one time x, two times y and one time z. After cutting the remaining is x / y. |
|---|

From your course professor I clearly know about the concept of variables and expressions.You explained to us about variables and expressions in a very simple way.
I studied these concepts only in matriculation. Then I did FSC Pre-Medical in Inter, so I didn't get a chance to do Maths in Inter. But I have learned a lot from your course.


I wrote an expression and now I solve it step by step.
= 15x + 6y - 10z equation (i)
The value of x, y and z are given below
x = 6
y = 5
z = 9
Putting the value of x, y and z in equation equation (i)
= 15x + 6y - 10z
= 15 (6) + 6 (5) - 10 (9)
I done multiplication in below
= 15 (6) + 6 (5) - 10 (9)
= 90 + 30 - 90
First addition in above
=120 - 90
Substraction in above
= 120 - 90
= 30

| From the course I clearly know about the concept of PEMDAS |
|---|
PEMDAS is also known as BODMAS
Let us take some examples and apply this rule to those examples.
 |
|---|
| Example 1! |
|---|
(A) Parentheses or Brackets
= 10 ÷ (5 + 3)
From the Rule PEMDAS first we solve inside the bracket.
= 10 ÷ (5 + 3)
= 10 ÷ (8)
First example solved.

 |
|---|
| Example 2! |
|---|
(B) Exponents or Orders
=4³
OR
= 4^3
= 4 × 4 × 4
= 64
Second example solved.
| Example 3! |
|---|
From the Rule the next step is Division and Multiplication
= 16 ÷ 4 × 5
= 16 divided by 4
= 16 ÷ 4 × 5
= (4) × 5
Multiply 4 × 5
=20
Third example solved.
| Example 4! |
|---|
From the Rule PEMDAS the next step is Addition and Substraction
= 15 + 5 - 10
So first I done addition
= 15 + 5 - 10
= 20 - 10
Then I done substraction
= 20 - 10
= 10
Fourth example solved.

| Task # 03 |
|---|
• Simplify this expression: 3(2x - 1) + 2(x + 4) - 5
• Evaluate this expression: (x^2 + 2x - 3) / (x + 1) when x = 2
• Solve the following equation: 2x + 5 = 3(x - 2) + 1

 |
|---|
From the equation mentioned in task 3
= 3(2x - 1) + 2(x + 4) - 5 equation (i)
Multiply by 3 and 2 in above equation (i)
= 3(2x - 1)
= 2(x + 4)
= 3(2x - 1) + 2(x + 4) - 5
= 6x - 3 + 2x + 8- 5 equation (ii)
| Addition and subtraction in above equation (ii) |
|---|
= 6x - 3 + 2x + 8- 5
= 6x + 2x + 8 - 3 - 5
= 8x + 5 - 5
= 8x + 0
= 8x
| Finally the expression is 8x |
|---|

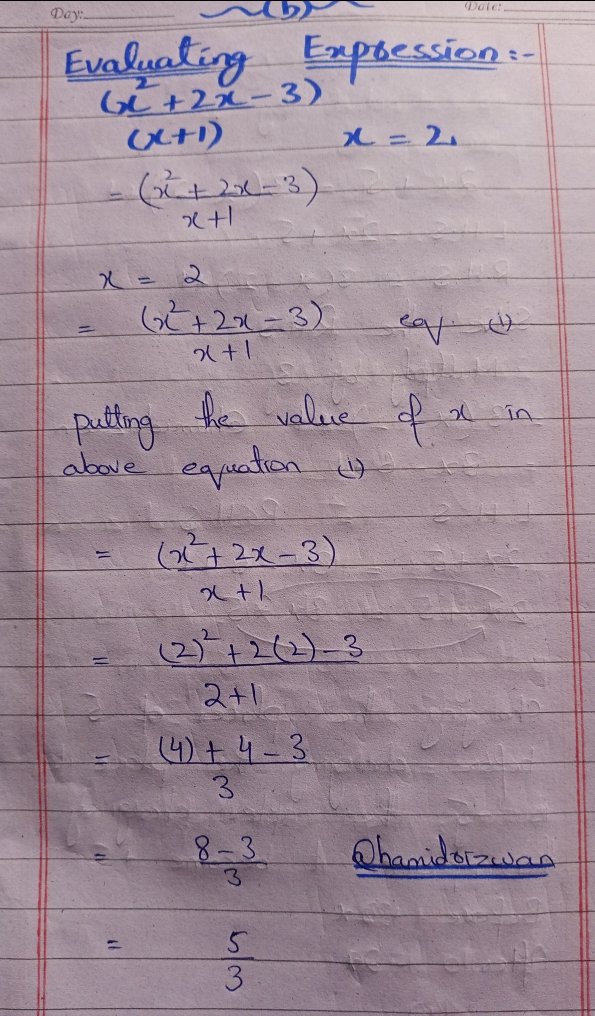 |
|---|
= (x^2 + 2x - 3) / (x + 1)
| According to question the value of x is mentioned and the value of x = 2 |
|---|
= (x^2 + 2x - 3) / (x + 1) equation (i)
Putting the value of x in above equation (i)
= (x^2 + 2x - 3) / (x + 1)
= (2^2 + 2(2) - 3) / (2 + 1)
= (4) + 4 - 3 / 3
= 8 - 3 / 3
= 5 / 3
| Finally the answer is 5 / 3 |
|---|

 |
|---|
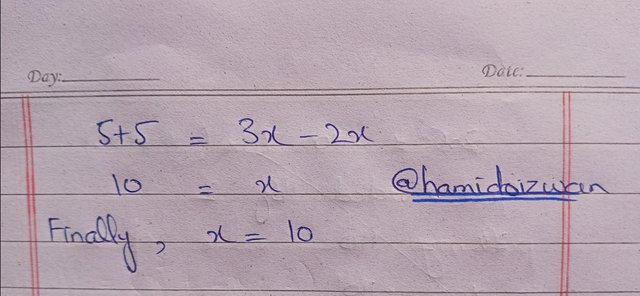 |
|---|
2x + 5 = 3(x - 2) + 1
L.H.S = 2x + 5
R.H.S = 3 (x - 2) + 1
I solved the R.H.S step by step in below
Multiply by 3
= 3 (x - 2) + 1
= 3x - 6 + 1
Combining the both i.e L.H.S and R.H.S
L.H.S = R.H.S
2x + 5 = 3x - 6 + 1
2x + 5 = 3x - 5
| Changing the position of 5 in R.H.S |
|---|
Before changing the position it is (-ve) 5, then after changing the position it becomes (+ve) 5.
***AND***
Before changing the position it is (+ve) 2, then after changing the position it becomes (-ve) 2.
5 + 5 = 3x - 2x
Addition in L.H.S and Subtraction in R.H.S
5 + 5 = 3x - 2x
10 = x
| Finally the answer is x = 10 |
|---|

• Suppose there's a bakery selling a total of 250 loaves of bread per day. They are selling whole wheat and white bread loaves with numbers of whole wheat loaves sold being 30 more than the number of white bread loaves. If x is representing number of white bread loaves sold out and bakery is making a profit of $0.50 for each white bread loaf and $0.75 for each whole wheat loaf then please write an expression for representing bakery total daily profit.

 |
|---|
 |
|---|
| According to Task |
|---|
White bread = x equation (i)
According to Task (numbers of whole wheat loaves sold being 30 more than the number of white bread loaves).
Therefore
Wheat loaves = x + 30 equation (ii)
| Total number of loaves mentioned in task 4 = 250 equation (iii) |
|---|
Combining of equation (i), (ii) and (iii)
x + (x + 30) = 250 equation (iv)
When we can see in above equation (i) (ii) and (iii) and we clearly know about equation (iv)
Then I start solving the equation (iv)
x + (x + 30) = 250
Addition of x + x = 2x
2x + 30 = 250
Changing the position of 30, before it is (+ve) 30 then after changing the position it becomes (-ve) 30.
2x + 30 = 250
2x = 250 - 30
2x = 220
Then I divided 220 / 2
2x = 220
x = 220 / 2
x = 110
| From equation (i) White bread x = 110 |
|---|
Putting the value of x in equation (ii)
Here x = 110
Wheat loaves = x + 30 (this is equation (ii)
= x + 30
= 110 + 30
= 140
| Hence proved that the total number of Wheat bread loaves sold is 140 |
|---|

 Step1 Step1 |
|---|
 Step2 Step2 |
|---|
 Step3 Step3 |
|---|
| According to task I clearly understand that the profit of white loaves is 0.50 $ |
|---|
So for x white loaves is 0.50 $ x
| Profit from whole wheat loaves is 0.75 $ per loaf |
|---|
So for (x + 30) whole wheat loaf the profit is 0.75 (x + 30)
Total profit = ?
Then I find total profit.
Total profit = Profit From White Loaves + Profit From Wheat Loaves
Putting values in above
= 0.50x + 0.75 (x + 30)
Here x = 110
Putting the value of x = 110 in above
= 0.50x + 0.75 (x + 30)
= 0.50 (110) + 0.75 (110 + 30)
In this step I done ✅ multiplication
= 0.50 (110) + 0.75 (110 + 30)
= 0.50 (110) + 0.75 (140)
= 55 + 105
= 160
From my answer the total profit is 160 $

| • Suppose that cost of renting a car for a day is re-presented by the expression 2x + 15 and here x is the number of hours in which car is rented. If the rental company offers a package of 3x - 2 dollars for customers who take car at rent for more than 4 hours then write an expression for the total cost of renting the car for x hours and show how you simplify it. |
|---|
| (Solve the above scenerio based questions and share step by step that how you reach to your final outcome) |
|---|
According to question 2x + 15 , where x is the number of hours the car is rented.
According to question 3x - 2 for customers whose take the car is rented for more than 4 hours.
2x + 15 is already simplified.
Now we can calculate the total cost?
Total cost = (2x + 15) + (3x -2)
| Total cost = 5x + 13 |
|---|

| Best Wishes 😍 Always be happy. |
|---|
Invite friends
@suryati1, @ishanto and @missyleo