Hi guys, you are welcome to my blog. Without any delay, let's attend to the questions presented by @khursheedanwar, I hope it will be fun...
 |
|---|
To understand what a variable is, we must first understand what Algeria is. Algebra is a combination of digits or numbers and letters or symbols. When a number, say 4, is written together with a letter, say m; 4m, it is called algebra.
In mathematics, variables are often letters used to represent a value. They are also used to represent an unknown quantity, value, or relationship in mathematical function, equation, or expression. a and z in 6a + 3z - 4 are variables. Variables can be dependent, independent, or controlled.
An expression, on the other hand, is the collection and combination of mathematical operations, variables, and numbers to form a mathematical statement. Examples of expression include:
2(3y + 5) - 6, 7 - 2(3 - 1)
An expression can include numbers, also known as constants, variables, which can be letters or symbols that represent unknown values, and mathematical operations like +, -, ×, ÷, etc; it can also include functions like sin, log, cos, and exponents like 2y², X², 3².
An expression like 2 + 3(3 - 1) has multiple operations and makes use of parentheses in prioritizing and grouping the calculation. This type of expression is called a Nested or Compound Algebraic Expression.
An expression like 4y + 3x(2 - 1) has coefficients 4 and 3, variables y and x, involves primary mathematical operations +, -, ×, and doesn't have any non-linear term like X². Such a type of expression is called Linear Polynomial Algebraic Expression.
When evaluating an algebraic expression in which the value of the variable is given, the steps I will take are as follows:
Let's consider:
Evaluate -2x - 2(3x - 4) - x, where x = 2
Solution
Since the value of the variable X is given as 2,
Step 1: Substitute x for 2
-2(2) - 2(3(2) - 4) - 2
= -4 - 2(6 - 4) - 2
Step 2: Clear bracket; which is the first order of BODMAS.
= -4 - 12 + 8 - 2
Step 3: Following the order of BODMAS, we carry out addition before subtraction
= -4 - 4 - 2
= -10
Our final answer is -10
There evaluating -2x - 2(3x - 4) - x, where x is 2 = -10
• ii. Evaluate this expression: (x^2 + 2x - 3) / (x + 1) when x = 2
• iii. Solve the following equation: 2x + 5 = 3(x - 2) + 1
(You are required to solve these problems at paper and these share clear photographs for adding a touch of your creativity and personal effort which should be marked with your username)
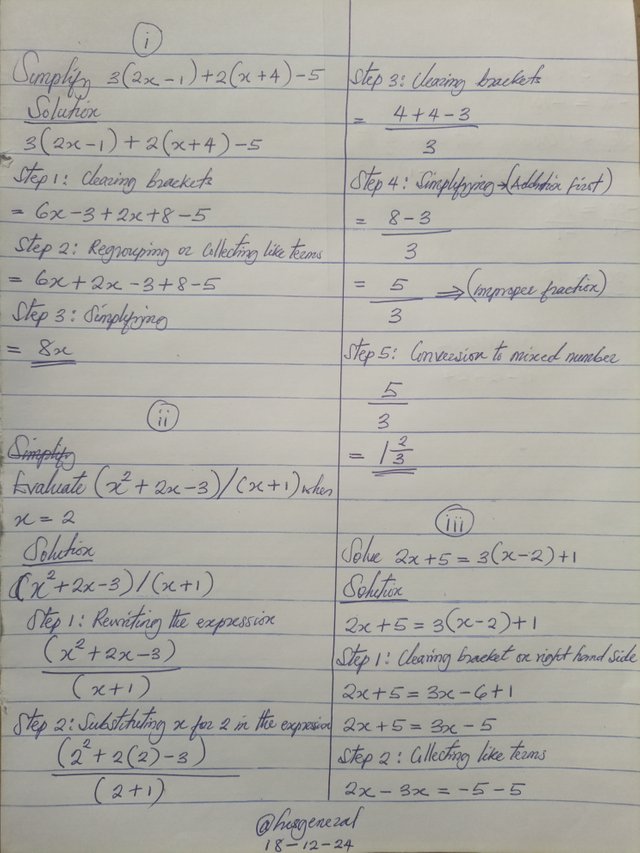

To write an expression that represents the bakery's total daily profit, we need to break down the information.
Total loaves sold = 250
White loaves sold = x
Wheat loaves sold is 30 more than white bread loaves
Wheat loaves = x + 30
Profit per white loaves = $0.50
Profit per wheat loaves = $0.75
Profit for total white loaves = x × $0.50
Profit for total wheat loaves = x + (x +30) × $0.75
Total profit = (number of white loaves × profit per white loaves) + (number of wheat loaves × profit per wheat loaves)
The expression representing the bakery's total profit will be:
(x × $0.50) + (x + (x +30) × $0.75)
Breaking the information down:
Daily rent = 2x + 15
Discount for 4 hours = 3x - 2
Since the company offered a discount for rent for more than 4 hours, then x is greater than 4
Therefore, total cost = Cost of rent - discount package = (2x + 15) - (3x - 2)
The expression for the total cost of renting the car for x hours is (2x + 15) - (3x - 2).
Solving for x in the expression (2x + 15) - (3x - 2)
Step 1: clear brackets
= 2x + 15 - 3x + 2
Step 2: collect like terms
= 2x - 3x + 15 + 2
= -x + 17
Am inviting @johnmitchel, @chiomi, and @divinelife
Your explanation is good, your breaking down of calculation is what one don't need to check again. Wishing you all the best in your entry ❤️👏.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit