Saludos amigos steemians.

El álgebra es una de las ramas más importantes para el estudio de las matemáticas, pues desde los niveles más básicos hasta los avanzados en el ámbito escolar hacemos uso de ella, por lo que me ha resultado muy interesante este curso y decidí hacerme partícipe del mismo.
Explicar dos tipos de variables y expresiones distintos a los que se explican en este curso.
Al hablar de Variable, se hace referencia a un símbolo que representa un valor cambiante dentro de una fórmula o ecuación, lo que significa que su valor puede cambiar. Estas se representan se representan de forma convencional con letras, sobre todo con la X y la Y.
Existen distintos tipos de variables dentro de los cuales se pueden mancionar las discretas y las continuas.
- Variables Discretas:
Estas son independientes y distintas, es decir que pueden ser contadas de forma individual. Por ejemplo, es posible contar el número de niños en un hogar, ya que puede haber 0, 3, 6, etc., pero no puede haber 3,45 hijos.
Otro ejemplo sería el número de dedos de pie y el número total de calcetines en un cajón; inclusive el número total de dedos en todos los pies de todas las personas en una ciudad es una variable discreta, tomaría mucho tiempo contar individualmente todos esos dedos, pero es posible hacerlo.
- Variables Continuas:
Son aquellas que conforman un todo ininterrumpido, es decir, que no se pueden contar en un tiempo finito porque hay un número infinito de valores entre dos valores dados.
Por ejemplo, si desea medir el tiempo, cada espacio de tiempo se puede dividir en unidades aún más pequeñas. El tiempo de viaje de un vehículo podría expresarse como 20,35 segundos, o podría desglosarse y expresarse como 20,35797565 segundos, y así sucesivamente, al infinito. Otros ejemplos de valores continuos incluyen la temperatura, la distancia y la masa.
Por otra parte, cuando se habla de Expresiones, se hace referencia al conjunto de números (constantes), letras (variables), que se combinan con los signos de las operaciones aritméticas. Existen distintos tipos de expresiones, entre ellos la fraccionaria y la radical.
- Expresión Fraccionaria:
Es aquella expresión que contiene fracciones dentro de una expresión algebraica. Por ejemplo:
6/x + 4/5
(x +5)/(x - 1 ) + 4
5/(x + 5) - 2/3
- Expresión radical:
Es aquella expresión que contiene un símbolo de raíz, como una raíz cuadrada, una raíz cúbica o una raíz cuarta. Por ejemplo:
3√(4) - 6
√(4x 5 ) + 2/3
√(x5 + 3x - 2)
Muestra tu forma de evaluar una expresión algebraica si se dan los valores de las variables.
Evualar una expresión algebraica cuando se conoce el valor de las variables es muy sencillo. Seguidamente explicaré de forma detallada la forma en la que realizo este proceso.
Lo primero que se debe conocer es la expresión a evaluar:
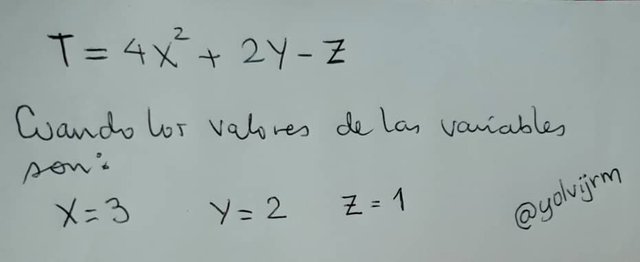
Como se puede apreciar en la imagen, la expresión está conformada por tres variables, cuyos valores son: X = 3, Y = 2, Z = 1
Es importante en este momento analizar cada elemento de la expresión algebraica, la cual en este caso viene dada por:
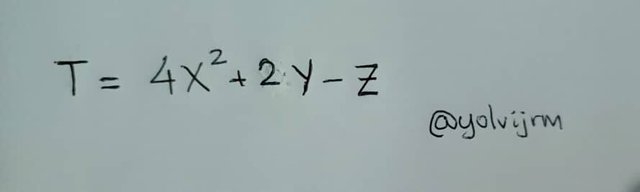
Seguidamente se procede a sustituir los valores dado para cada una de las variables, lo cual quedará expresado de la siguiente manera:

Ahotra viene la simplificación del término en donde se encuentra la potencia, que en este caso es al cuadrado (2).
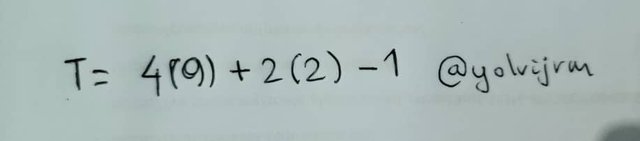
Posteriormente se procede a realizar la multiplicación simplificando los términos.
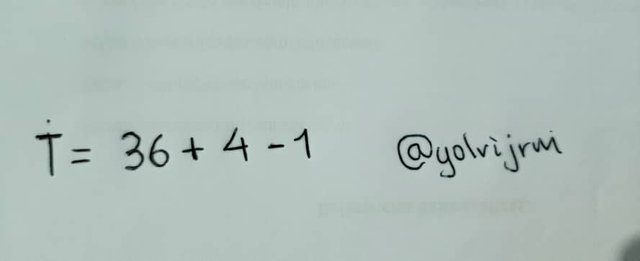
Por último se realizan las operaciones de suma y resta que contiene la expresión:
Sumar: 36 + 4 = 40
Restar: 40 - 1 = 39
Por tanto T = 39
Simplifica esta expresión: 3(2x - 1) + 2(x + 4) - 5

Para simplificar esta expresión, primeramente expandí el término que se encontraba fuera del paréntesis, aplicando la propiedad distributiva de la multiplicación, en cada uno de los términos. Seguidamente, se agruparon los términos semejantes que involucraban a X y las constantes, lo que conllevó a obtener un resultado de 8X.
Evalúa esta expresión: (x^2 + 2x - 3) / (x + 1) cuando x = 2

En esta actividad, lo primero que se realizó fue la sustitución del valor de X, tanto en el numerador como en el denomidador, para posteriormente realizar las operaciones correspondientes en cada uno de los términos, obteniendo un resultado de 1,6.
Resuelve la siguiente ecuación: 2x + 5 = 3(x - 2) + 1

En esta actividad, lo primero que se realizó fue aplicar la propiedad distributiva de la multiplicación en el lado derecho, distribuyendo el 3 en x - 2, y seguidamente se simplificó realizado las operaciones correspondientes. Por último como la X tenía signo negativo, se multiplicó ambos miembros de la ecuación por -1
Supongamos que hay una panadería que vende un total de 250 panes al día. Se venden panes de trigo integral y pan blanco, y la cantidad de panes de trigo integral vendidos es 30 veces mayor que la cantidad de panes de pan blanco. Si x representa la cantidad de panes de pan blanco vendidos y la panadería obtiene una ganancia de $0,50 por cada pan blanco y $0,75 por cada pan de trigo integral, escriba una expresión que represente la ganancia diaria total de la panadería.
De acuerdo a lo planteado se tiene que x es el número de panes blancos vendidos; por tanto x + 30 representaría el total de panes integrales que se venden. Además se conoce que 250 es el total de panes vendidos por día; por tanto:
x + (x + 30) = 250
Realizando la simplificación, se tiene:
2x + 30 = 250
2x = 250 - 30
x = 220 / 2
x = 110
Este resultado X = 110, implica que esta es la cantidad de panes blancos vendidos, por tanto 110 + 30 = 140, corresponde al total de pan integral vendido.
Entonces, se tiene que la expresión de la ganancia viene dada por:
Ganancia por pan blanco = $0,50
Ganancia por pan integral = $0,75
Ganancia total = (0,50x) + (0,75(x + 30))
Simplificando la expresión, sustituyendo los valores, se tiene:
Ganancia total = 0,50x + 0,75x + 0,75(30)
Ganancia total = 1,25x + 22,5
Supongamos que el costo de alquilar un automóvil por un día se representa mediante la expresión 2x + 15 y donde x es el número de horas en las que se alquila el automóvil. Si la empresa de alquiler ofrece un paquete de 3x - 2 dólares para los clientes que alquilan el automóvil durante más de 4 horas, escriba una expresión para el costo total de alquilar el automóvil durante x horas y muestre cómo la simplifica.
Lo primero que se debe realizar es escribir la expresión del costo de alquilar el auto por x horas que quedará expresada como 2x + 15
Se tiene que el costo adicional del paquete por más de 4 horas de alquiler será de 3x - 2, por lo tanto:
Costo total = (2x + 15) + (3x - 2)
Ahora se procede a simplificar la expresión combinando los términos iguales, y realizando las operaciones correspondientes:
2x + 15 + 3x - 2
2x + 3x + 15 - 2
5x + 13

Gustoso de presentar mi participación en este concurso; aprovecho la oportunidad de invitar a @graceleon, @fjjrg y @naka05 a que participen en esta actividad:
SLC S22W1//Variables and Expressions
Las imágenes son de mi propiedad, tomadas con Infinix Note 40 Pro.
Cc: @khursheedanwar
¡Saludos y bendiciones!
