_{designed using canva}

As we discussed in last class, equation describes the relationship between variables. From the name Linear, a line graph comes to our mind and we hear of one but when quadratic is mentioned, X² comes to our mind where we would find two numbers to get the values of X. Linear and quadratic equations differ extensively in structure, degree, graphical representation, how it's solved and applied. I'll be specific while giving the differences of these two terms.

Definition

Linear Equation: is an equation where the highest power of the variable which can be dependent or independent is 1 or raised to the power of 1. It is usually represented as.....

2x + 3= 4

Where;
x is the dependent variable
x has a power of 1 but is invisible x¹
It is equal to 4 which makes it an equation.

It has a general form....

ax + b = 0 where a ≠ 0

Quadratic Equation: is an equation where the dependent variable has the highest power of 2. Its variable which could be X or Y has the highest power of 2 while the polynomials includes; x³, x⁴,..xn. It has a parabolic graph when drawn while that of linear has a linear structure, straight line graphed.

It could be represented as;

3x² + 4 + 6 = 0
Where;

x has a highest power of 2
x² is dependent on 3

The general form is

ax² + bx + c = 0
where a ≠ 0

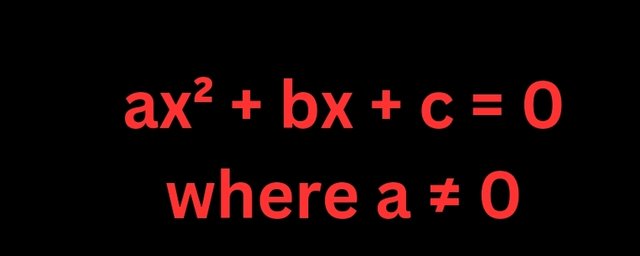
In this general form, we can outrightly see that a is the constant value that makes the variable with a power of 2 dependent and that power of 2 makes it quadratic. You can see a variable raised to a power of 1 or 3 and call it quadratic.

Variables and Degrees

Linear Equation as explained earlier usually have just one degree of which the variable is raised to the power of 1. In representation, it can contain more than one variables because of its method of solving.

E.g:

A linear equation can have x + y, xy + xz etc

Quadratic Equation as explained earlier follows a regular pattern where just one variable is used in conjunction to the powers of each variable. It's more like a descending order in powers of a particular variable. It has just two degrees with which is represented as x².

The order.....is from the highest power of quadratic which is 2, to the lowest which is 1.

2x² + 5x + 7 = 0

In real life, linear equation is applied in solving problems concerning speed of a vehicle, cost etc while p

Categories	Linear	Quadratic
Degree	1	2
Representation	3x + 2 =0	3x² - 5x + 1 = 0
Variables	one or more variables	only one variable
Graph	Straight line graph	Parabolic Graph

Practical Examples

Linear Equation: Having one degree and can have more than one variable, its way of solving depends on where it appear but still one way. E.g: 5x - 6 = 4

_Looking at this equation, we have unlike terms there in . We need to take like terms to where we can find them and find the value of X. In both, we do find the value of variables. In Linear, it could be just X or x and y. In quadratic, it could either be X or Y.

5x = 4+6
5x = 10
5x/5 = 10/5
x = 2
The value for X is 2

Quadratic Equation: Has two degrees on its variable and we still look for the values of x. In quadratic, we usually look for two numbers that gives us the value of X. An interesting quadratic, we can use different methods in getting the answer which could be factorisation, completing the square method and almighty formula or quadratic formula. E.g x²+4x-5=0

x²+4x-5=0

Using factorisation method, we'll need to look for the two numbers that when you multiply, it would give you -5 and when you add, it would give you +4. We look for two factors of 5 which is 1 and 5 itself. So let's play with it.

1 × -5 = -5	1 - 5 = -4	❌
1 × 5 = 5	1 + 5 =6	❌
-1 × -5 = 5	-1 - 5 = - 6	❌
- 1 × 5 = - 5	-1 + 5 = 4	✅

Two numbers there are ( -1 and 5). Now, in place of 4x, we'll substitute -1x and 5x.

x² - x + 5x - 5 = 0
(x² - x )+ (5x - 5 )= 0

Factorising x which is common in the brackets.

x ( x - 1) + 5 (x - 1) = 0
The common values here are (x-1) (x + 5)
Equating the factors to zero, we have.

x - 1 = 0	x + 5 = 0
x = 1	x = -5

So the values of X in the question are -5 and 1. To check, you'll need to substitute it in the main equation to know if your factors are correct.

x²+4x-5=0

For x = 1

(1)² + 4(1) - 5

1 + 4 - 5 = 0 ✅

For x = 5

(5)² + 4(5) - 5

25 - 20 - 5

5 - 5 = 0 ✅

Describe two different types of inequalities(Which are not explained in course). Provide examples of each type of inequality and explain how to solve them.

There are various types of inequalities used to show how unequal items can be in conjunction with another. The two types of inequalities I'll be talking about are the;

Polynomial and rational inequalities

These two types of inequalities are used extensively in solving complex mathematical problems as they describe the relationship between values where one item is greater, less or not equal to the other.

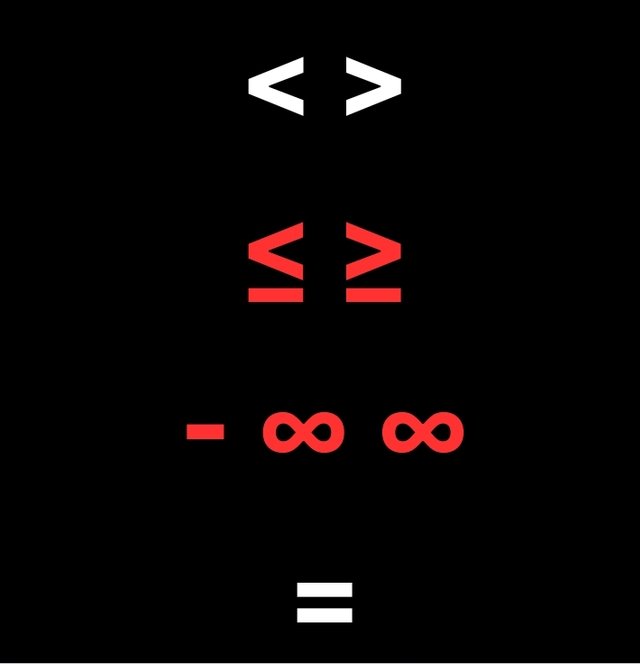
Polynomial Inequality is most times likened to hills and valleys where the height differs from each other. Polynomial inequality involve polynomial expressions where the highest power of the variable involve is greater than one. It's more like the definition of linear and quadratic equation but differs because inequalities mainly use signs like......

< >
<
=
≥
≤
≠
∞

Polynomials naturally are expressions made by adding or subtracting variables like y raised to the powers starting from 3 or more as first digit. An inequality occurs in this Polynomial expression when we start comparing the Polynomial involved to zero using the signs mentioned above. In this case, it's more like solving the Polynomial but the value of X must be found and it must either be greater than, less than, greater than or equal to 0, depending on what sign you're given. A typical example is;

You're given x³ + 4x² - x > 0. We're to find points where the values of x is greater than zero and also check intervals that satisfies the inequality to be sure it's correct from the number line. We'll have to test all numbers to know if they'll give us values greater than zero.

On our number line, we have - ∞ to + ∞. This is the range we would used in testing the above. Let's start with - ∞ testing of the Polynomial.....x³ - 4x² + x

Let's use - 1 to test if the negative terminals work for the Polynomial.

(-1)³ - 4(-1)² + (-1)

-1 - 4 -1

-6....This value is less than zero which doesn't satisfy the Polynomial ❌❌❌. The - ∞ is out of the game. Let's try 0...

For x = 0 ........x³ - 4x² + x

(0)³ - 4(0)² + (0)

0 - 0 + 0.......0

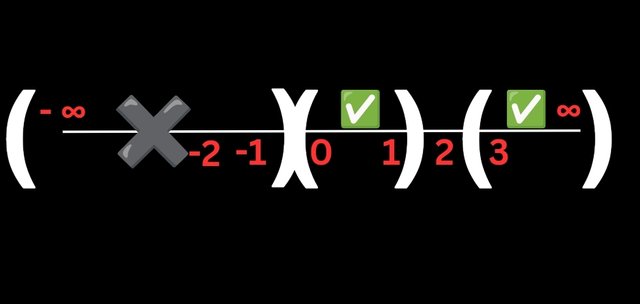
This satisfies it ✅✅✅😉 (0)
The interval of 0 - 1 can satisfy it as if we want to try 1, it won't be satisfied.

For x = 2, it won't satisfy as they'll be a negative sign. For x =3, it won't satisfy but 3.6 can satisfy. So the range would be from 3 to infinity as 4 and other numbers can satisfy the Polynomial.

x³ - 4x² + x

(4)³ - 4(4)² + (3)

64 - 64 ** + 3

3........ Satisfies it ✅✅✅

So we have our intervals from (0, 1) U (3, ∞). Our answer from the number line if the Polynomial is greater than zero.

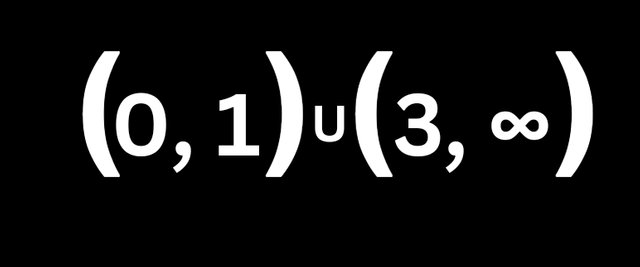
Rational Inequality:

Rational inequality is a fraction where both the numerator and the denominator determine the weight on each side. You're checking where the balance is stable and this is usually the case when you have signs that is greater than, less than, greater than or equal to zero or any other number. Let's take this example...

x - 3 /x +2 ≥ 0

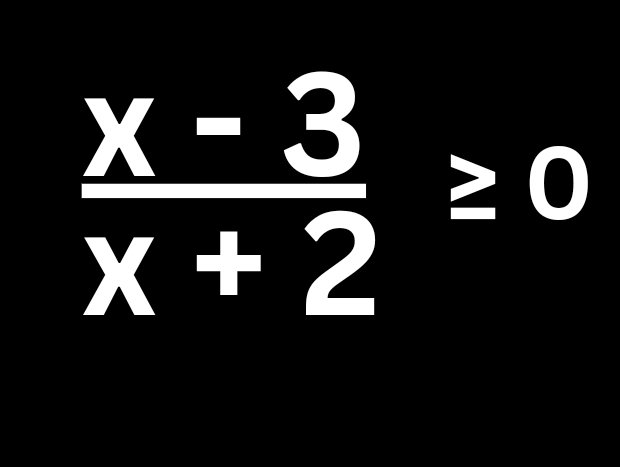
Let's set the numerator and denominator to zero to get the actual value range of x.

x - 3 = 0

x = 3...... Numerator

x + 2 = 0
x = - 2 ...... Denominator

Now we've gotten our range of values to use for the number line in determining what satisfies the inequality. Since the number line is not written as text but expressed in the picture below, let's work on the range from -∞ to -2 to 3 to ∞

Now let's work on the values from - ∞ to - 2..

For x = - 4

-4 + 1/- 4 - 2 = -3/6..
If we are to divide it, we'll have a positive fraction which is greater than zero as implied in the inequality.

In the case of rational, the numerator and the denominator must attain a balance of either positive or negative values. Where the Numerator is zero, it makes the fraction zero but when the denominator is zero, the fraction becomes undefined.

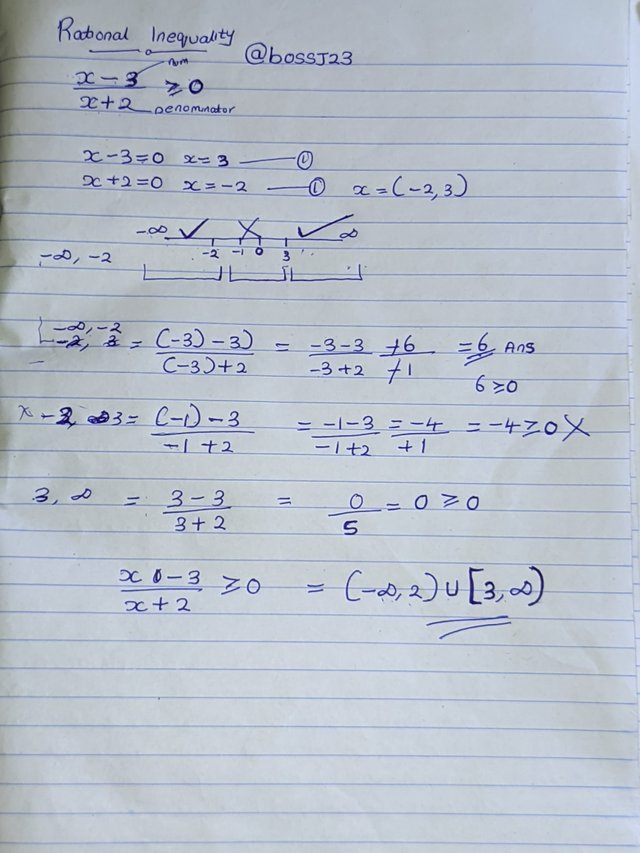
If we use the values from - ∞ to -2, we'll see that the values have attained a balanced of negative signs in the numerator and denominator. So they satisfy the inequality as we have values greater than zero.

Let's check for -2 to 3

For x = -1

x - 3 / x + 2 = -1--3 / - 1 + 2 = -2/+ 1 This doesn't satisfy the inequality as the complete simplification of the fraction gives us -2 which is less than zero and not greater than.

If we're to solve x = 4,

x -3 /x + 2 = 4-3/4+2

The answer which is 1/6 is greater than zero on the number line. The points that satisfies the inequality can be represented as.

(-∞, -2 ) U [3, ∞).....

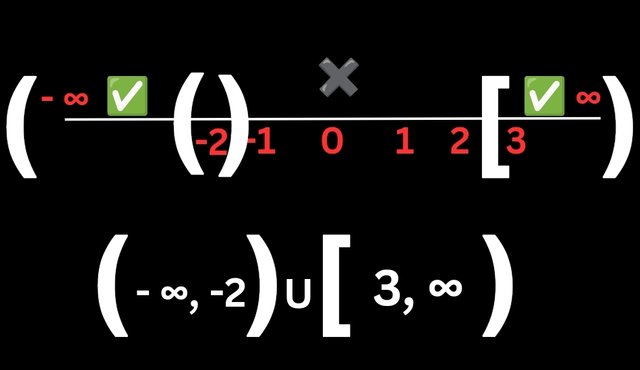
Solve the following linear equation: 2x + 5 = 11.Show step-by-step solution and share its practical example of how this equation can be applied in real life scenario.

Last tutorial, we were taught equations and how to solve simple and complex equations. For the purpose of this question, I'll be solving it in a way that anyone can understand even though you weren't part of the last class.

The equation given is 2x + 5 = 11. This equation is Linear because the degree of the X variable is 1. To solve this effectively, we need to understand that this equation consists of like and unlike terms.

We can't add 5 with 2x as they are not relative. So we'll take them to their houses as there's a barrier between the unlike terms in the presence of just one like term which matches just one side.

It's just like taking a seeing an 8 year old boy in SS3 but his class is primary 3. You won't allow him be in that class with grown ups as his size or she mates aren't in that class. He is unlike with those students in SS3 but he has his likes in primary 3. To solve this problem, he must be taken out of SS3 to primary 3.

Solution

2x + 5 = 11......Linear

Step 1: Identify which equation it is and solve for X.

It's a linear equation and the value of X can be determined by collecting Like terms so the x variable can stand on its own.

Step 2: Collect Like Terms

So we'll be taking 5 to meet 11 as 5 is in 2x class and 2x is bigger than him 5. To do this in mathematics, we collect like terms.

2x + 5 = 11

2x = 11 - 5

Once 5 crosses the equality sign, his own sign which is + changes to minus and we do the calculations.

2x = 6

Step 3: Find x by dividing both sides by the coefficient of X.

We still have two unlike terms in opposite sides. We need to find the value of x using 6. We need to remove the 2 in front of the X variable. How do we do this? We divide both sides by the coefficient of X which is 2.

2x /2 = 6/2
x = 3

To check if your answer is correct, substitute X for 3 in the equation.....2x +5 = 11

2(3) + 5 = 11
6 + 5 = 11

We have 11 as the final answer which means the equation and the value for X are correct.

The value of X which was missing is 3. How is this equation applied in real life? Let's just imagine two friends decide to share the expenses that would be incurred in a beach party. Since this is to be shared, there must be a balance between of expenses as to the price or cost to avoid cheating anyone.

They hired a vehicle that would transport them to the venue. This driver charged them 5 steems and an additional 2 steems for who joins the transportation. In total, the spent a total of 11 steems for transportation. The question is how many people joined the vehicle?

Remember...

Transport fare is 5 steems which is constant
Cost for each person entering the vehicle is 2 steems multiplied by the number of persons which is unknown, x.

Total cost for transportation is 11 steems.

2x + 5 = 11. If we're to solve the mathematical problem using the above, we'll have it that 3 people joined the transport fare. So the equation is solved. If you fix 3 in place of 3 and solve, you'll have 11.

2(3) + 5 = 11. You can use this step to check if your answer is correct.

Task 4

Tom's bakery is a most famous bakery of tow and it's famous for its yummiest pastries and bread. Tom which is owner want for making sure that he has sufficient ingredients for meeting needs for his famous chocolate cake and chocolate cake recipe needs 2 cups of flour, 1 cup of sugar and 1/2 cup of cocoa powder for each cake.

Forming an equation would require considering the ingredients needed for each cake as well as the total amount of available ingredients.
• Flour: 2 cups per cake, available cups = 10
• Sugar: 1 cup per cake, available cups = 8
• Cocoa powder: ½ cup per cake, available cups = 4

We can derive the following equations:
• Flour => 2x ≤ 10
• Sugar => x ≤ 8
• Cocoa powder => (½)x ≤ 4

These equations need to be solved to find the number of cakes Tom can make
Solution
• Flour:
= 2x ≤ 10
= 2x ≤ 10
= x ≤ 10/2
= x ≤ 5

Sugar:
x ≤ 8

• Cocoa powder
(½)x ≤ 4
= ½x ≤ 4
= x ≤ 4/½
= x ≤ 4 × 2/1
= x ≤ 8

x = 5 is the least value of x, which satisfies the three equations.

Therefore, with the available ingredients, Tom can make at least 5 cakes.

First, we need to define the variable, so let x be the number of cakes he intends to make.

The next step is to form an inequality
Since each cake requires 1 cup of sugar and Tom has 8 cups of sugar, the inequality will be:
x ≤ 8

Nevertheless, Tom also intends to make at least 6 cakes, so this will require forming a compound inequality:
6 ≤ x ≤ 8

The final step will be to solve the inequality
Solution
This is simply all values of x between 6 and 8, inclusive.

Therefore, with the available sugar, Tom can make at least 6 cakes and, at most, 8 cakes.

In scenario 2, we need to understand something here. These includes the amount of flour , sugar and the cocoa powder used in baking the bread.

Flour	2 cups per cake
Cocoa	½ per cake
Sugar.	1 cup per cake.

If Tom wants for making x cakes and he has 10 cups of flour, 8 cups of sugar and 4 cups of cocoa powder then calculate number of cakes that can be made by Tom?

Taking these into consideration, we have;

Sugar as x ≤ 8...I e the x variable is multiplied by the constant.

Flour as 2 is multiplied by x.

2x ≤ 10
2x/2 ≤ 10/2

x ≤ 10/2

x ≤ 5......Flour

Cocoa has a constant of ½ and is multiplied by the x variable.

(½)x ≤ 4

Divide both sides by the coefficient of X.....

½x/½ ≤ 4/½

x ≤ 4 × 2/1

x ≤ 8

The least value among the ingredients is that if flour which is 5 and satisfies the equation is put in place of x.

5 ≤ 8

5 ≤ 5

Having known these, Tom can make at least 5 cakes.

To get the inequality aspect which is the possibility......The inequality would be that since each cake needs one cup of sugar but Tom has 8 cups of sugar. He intends to make just 6 cakes which makes the inequality bounce on the range of 6 ≤ x ≤ 8. With this inequality, Tom can make at least 6 cakes with what's available and at most 8 cakes still with what's available. The signs read it all.

Second Scenario

Suppose there's a person named Ashley who is planning a road trip from City A to City B. If I talk about distance between two cities then it's around 240 miles. Ashley's car fuel tank can hold 12 gallons Suppose that his car gets 20 miles for each gallon then how many gallons of gas may Ashley purchase if he already has 2 gallons in his tank and he wants to have a minimum of 1 gallon left over when he arrives at City B?

Let X be the number of gallons of gas Ashley can purchase.

Parameters:
Total distance covered = 240 miles
Total required gas = 240/20 = 12 gallons
Miles per gallon = 20

From the question, Ashley already has 2 gallons left and and 1 gallon as leftover.

The sum of the gas she has is 2 gallons and the gas she purchase would be x. Her tank holds only 12 gallons of gas. Combining the values of total gallons, leftover and the one she has, we'll have;

2 + x + 1 ≤ 12

In this case, we'll take all like terms to the right hand side while we find the value of X and then check if it fits.

Collect like terms

2 + x + 1 ≥ 12

x ≥ 12 - 2 - 1

We all know when the sign a constant bears crosses the equals sign, it changes.

x ≥ 12 - 3
x ≥ 9

Since x ≤ 9, Ashley can now purchase 9 gallons of gas

Possibility to check

x + 2 ≥ (240/20) - 1
x + 2 ≥ 12 - 1
x ≥ 12 -1 - 2
x ≥ 9

She can now purchase at least 9 gallons of gas

Cc,
@khursheedanwar

I invite @basil20, @whizzbro4eva and @aviral123

"SLC-S22W2/Equations and inequalities."

Definition

Variables and Degrees

Practical Examples

Second Scenario