Invito a participar en el concurso "SLC S22W3//Equations and Systems of equations" a los amigos @ahsansharif @suboohi y @shuhad.

Los sistemas de ecuaciones son lineales cuando la la mayor potencia de las variables involucradas es igual a 1, es decir, al representarlos en un sistema se coordenadas, su gráfica es una línea recta, siendo su forma general como se muestra a continuación.
2x + 2y = 5
X - y = 3
Si el mayor exponente de la variable es mayor que 1, el sistema de ecuaciones ya no es lineal y al representar su gráfica en un sistema de coordenadas no resulta ser una línea recta, sino que su grado del sistema de ecuaciones quedará definido por la variable que tenga la mayor potencia, por ejemplo si la potencia es 2, se dice que el sistema de ecuaciones es cuadrática y su gráfica en un sistema de coordenadas quedará representada por una parábola.
Su forma general viene dada de la siguiente manera.
X2 - Y2 - 9 = 0
X + y = 4
Existen varios métodos para la resolución de sistemas de ecuaciones, entre los que destacan el método de sustitución de variables, eliminación, el método gráfico y el método de cramer.
En esta sección estaremos explicando de manera detallada el método de cramer para la resolución de sistemas de ecuaciones que es distinto a los métodos en esta clase, pero antes vamos a presentar la resolución del mismo sistema utilizando el método de la sustitución de variables a manera de contrastar los resultados obtenidos por ambos métodos..
Método de sustitución
El método de sustitución consiste en poner una de las variables o incógnitas en función de otras variables y luego se sustituye en la otra ecuación, lo que permite aislar o despejar una variable para obtener su valor, y luego con el valor obtenido se sustituye y se obtiene la otra variable del sistema.
Para ambos casos se resolverá el siguiente ejercicio:
2X - y = 4 ...... (1)
X- y = 3 ......... (2)
Aplicando el método de sustitución, tomamos la ecuación (2) y ponemos la variable "x" en función de "y".
X = y + 3
Luego se sustituye "x" en la ecuación (1), de la siguiente manera:
2 (y+3) - y = 4
Multiplicando y sumando queda:
2y + 6 - y = 4
y = 4 - 6
y= -2
Luego el valor de la variable "y" obtenido se sustituye en la ecuación (2) y se obtiene la variable "x".
X - y = 3
X -(-2) = 3
Aislando el valor de "x" se tiene:
X = 3 -2
x =1
Entonces la solución a el sistema de ecuaciones es { x=1 ; y = -2}
Método de cramer
Este método utiliza los detalles determinantes como herramienta de cálculo para determinar el valor de cada una de las variables del sistema de ecuaciones, el método consiste básicamente calcular el determinante de cada variable por separado para luego dividirlo entre el determinante del sistema, con lo cual se obtiene el valor de la variable en cuestión, repitiendo el proceso según el número de variables que tenga el sistema.
En tal sentido, si se tiene un sistema de dos ecuaciones y dos variables o incógnitas como el, el procedimiento de cálculo es el siguiente:
2X - y = 4 ...... (1)
x - y = 3 ......... (2)
En primer lugar se calcula el determinante de la matriz del sistema de ecuaciones dado por las variables "x"" e "y" con los números o coeficientes que acompañan a las variables como se muestra en la siguiente imagen.
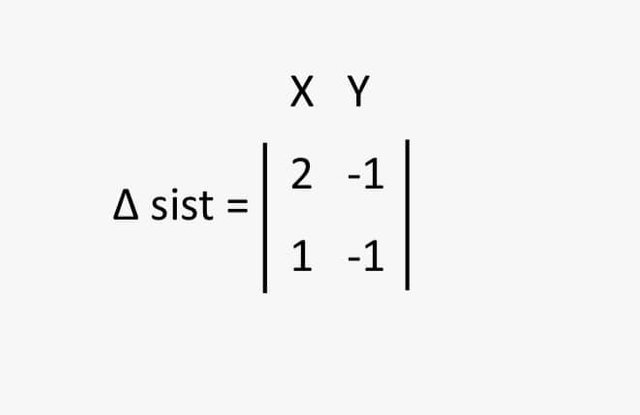
Resolviendo el determinante, Multiplicando y sumando las diagonales queda:
Determinante sistema = Det sist.
Det sist = (2 * -1) - (-1 * 1)
Det sist = -2 +1
Det sist = -1
Una vez que se tiene el valor del determinante del sistema, se procede a calcular los determinantes de las variables "x" e "y" de la manera siguiente:
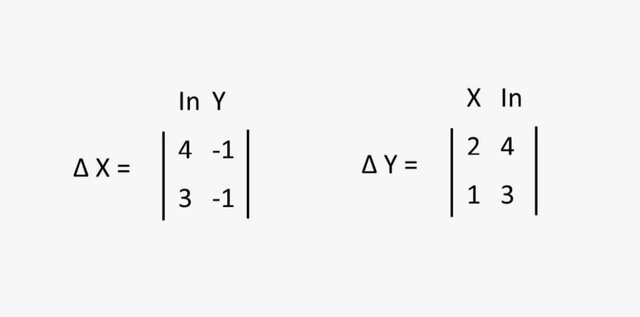.jpeg)
Si observa la imagen, el término "In" se refiere a la fila del término independiente, por lo que para calcular el determinante de la variable "x", se sustituye en el determinante en el lugar de la variable "x", dicha fila de términos independiente y se procede a resolver de la misma forma que el Det sist.
Det x = (4 * -1) - (-1 * 3)
Det x = -4 +3
Det x = -1
Luego, aplicando el mismo procedimiento se calcula el determinante la variable "y", pero en el lugar de la fila de "y" se sustituye la fila del término independiente como se observa en la imagen anterior:
Det y = (2 * 3) - (4 * 1)
Det y = 6 - 4
Det y = 2
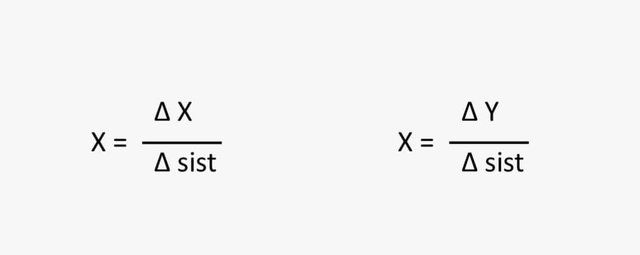.jpeg)
Finalmente, después de de calcular los determinantes del sistema y de las variables "x" e "y", se procede a determinar los valores de la variables por medio de la relación dada en la imagen anterior:
Entonces dividiendo se tiene:
X= Det x / Det sist
X = -1 / -1
X= 1
Y= 2 / -1
Y = -2
Con lo que se demuestra que la solución del sistema de ecuaciones es:
{X= 1 ; Y=-2}
(a)
x + 2y = 7
3x - 2y = 5
.jpeg)
(b)
4x + 6y = 2
x - 2y = 3

Escenario número 1
Supongamos que hay una empresa que produce dos productos, A y B. Si el coste de producir x unidades de A e y unidades de B está dado por el sistema, entonces:
2x + 3y = 130 (costo de materiales)
x + 2y = 110 (costo de mano de obra)
Si la empresa quiere producir 50 unidades del producto A, calcule cuántas unidades del producto B puede producir.
(Resuelva las preguntas basadas en el escenario anterior y comparta paso a paso cómo llegar al resultado final)
Escenario número 2
Supongamos que hay una panadería que produce dos tipos de pasteles, de vainilla y de chocolate. Si el costo de producir x pasteles de vainilla e y pasteles de chocolate está dado por el sistema, entonces;
x + 2y = 80 (costo de los ingredientes)
2x + y = 70 (costo de la mano de obra)
Si una panadería quiere producir 30 pasteles de vainilla, calcule cuántos pasteles de chocolate puede producir.
Al tratar de resolver los sistemas de ecuaciones dados en los escenarios 1 y 2, se obtienen valores inconsistentes de las variables carentes de toda lógica, lo que indica que tal como se ha planteado el sistema de ecuaciones, las variables no se pueden relacionar entre sí, por lo tanto dicho sistema no tiene solución lógica posible.
En tal sentido, analizando cada ecuación por separado se puede llegar a conclusiones congruentes y más adaptadas al campo de la lógica.
Escenario 1.
2x + 3y = 130 (costo de materiales) .... (1)
x + 2y = 110 (costo de mano de obra)...(2)
Se quiere producir 50 unidades de A, entonces de la ecuación 2 de mano de obra se tiene:
x + 2y = 110
50 + 2y = 110
2y = 110 - 50
2y = 60
Despejando y queda:
y = 30
Luego de la ecuación de materiales
2x + 3y = 130
Sustituyendo x=50
2(50) + 3y =130
3y = 30
Despejando se obtiene la cantidad de productos B será:
y = 10
Interpretando los resultados se puede decir que por mano de obra hay disponibilidad para producir 50 productos de A y 30 de B.
Sin embargo por la ecuación de materiales sólo se pueden producir 50 unidades de A y 10 de B, lo que indica que la limitante en este caso son los materiales, por lo que la cantidad de productos B que se pueden producir será 10 solamente.
Escenario 2.
x + 2y = 80 (costo de los ingredientes)....(1)
2x + y = 70 (costo de la mano de obra)....(2)
En la ecuación 2 de mano de obra, se sustituye x=30 que es la cantidad de helados de vainilla que se desean producir,
X+ 2y = 80
30 + 2y =80
2(30) + y =70
Sumando y despejando se obtiene que la cantidad de helados chocolate a producir por mano de obra es:
Y=10
Luego se sustituye x=30 en la ecuación de ingredientes (2) y se obtiene
x + 2y =80
30 + 2y =80
2y = 80 -30
Despejando queda la cantidad de helados de chocolate a producir es:
Y=25
Interpretando los resultados obtenidos, se puede concluir que por costos de mano se pueden producir 10 helados de chocolate, mientras que por la ecuación de ingredientes sólo pueden producir 25 helados de chocolate, por lo que la limitante para la producción, por lo que en este caso lo que limita la producción es la mano de obra , por lo que la cantidad de helados de chocolate a producir es de 10.
Sin más que agregar queridos steemians, me despido, espero les haya gustado la publicación, hasta la próxima oportunidad.
Las fotografías son de mi propiedad, tomadas con un teléfono Samsung Galaxy A30.
Para saber más de mí, aquí dejo mi Logro1.