Greetings ,
This is @artist1111. I hope you are all doing great! Today, I am super excited to sharing my assignment on Linear and Quadratic Equations. The lecture was both engaging and informative, and truly I am thrilled to showcase my learning and the work I’ve completed.

Explain difference between linear and quadratic equations. Provide examples of each type of system of equation and describe their general forms.
Difference Between Linear and Quadratic Equations
Linear and quadratic equations differ primarily in the degree of their variables and their graphical representation.
Linear Equations
A linear equation is equation where the highest power of the variable which is 1. These represent straight a lines on a graph. They involve a constant rate of the change and it typically describe simple, proportional relationships.
General Form:
ax + b = 0
where a and b are constants, and x is the variable.Example of a Linear Equation:
2x + 3 = 7
Solving for x:
x = 2System of Linear Equations:
A system involving multiple linear equations:
y=x^2 +2x−3
These can be solved using substitution, elimination, or graphing methods.
Quadratic Equations
A quadratic equation is one where the high power of the variable and it is 2. These equations form a parabola when graphed & are often used to model curved relationships such as trajectories or areas.
General Form:
ax^2 + bx + c = 0
where a ,( b , and c are constants, and x is the variable.Example of a Quadratic Equation:
x^2 - 4x + 4 = 0
Solving using factoring:
(x - 2)(x - 2) = 0
x = 2System of Quadratic Equations:
A system with at least one quadratic equation:
y = x^2 + 2x - 3
y = 2x + 1
These systems can be solved using substitution or graphing to find points of intersection.
Key Differences
| Aspect | Linear Equations | Quadratic Equations |
|---|---|---|
| Degree | 1 | 2 |
| Graph | Straight Line | Parabola |
| Rate of Change | Constant | Varies |
| Form | ( ax + b = 0 ) | ( ax^2 + bx + c = 0 ) |
| Example | ( 3x + 2 = 8 ) | ( x^2 - 5x + 6 = 0 ) |
Task 2
Describe methods for solving quadratic equations and share pros and cons for each method.
Quadratic equations can be solved using several methods, each with its own advantages and disadvantages. Here’s an overview of the main techniques:
1. Factoring
This method involves expressing the quadratic equation as a product of two binomials.

2. Quadratic Formula
The quadratic formula is a universal method applicable to all quadratic equations:

--
3. Completing the Square
This method involves rewriting the equation into a perfect square trinomial.

4. Graphing
Graph the quadratic equation and identify the points where it crosses the x-axis (if any).
Process:
Graph (y = ax^2 + bx + c).
Find the x-intercepts, which are the solutions.Example:
Graph (x^2 - x - 6 = 0):
The graph crosses the x-axis at (x = -2) and (x = 3).
Pros and Cons
| Method | Pros | Cons |
|---|---|---|
| Factoring | Simple and quick for factorable equations. | Limited to equations that are easily factorable. |
| Quadratic Formula | Universal and works for all quadratics. | Lengthy for simple equations; requires computation. |
| Completing the Square | Useful for equations that are not factorable. | Time-consuming and requires additional steps. |
| Graphing | Visual and intuitive for understanding solutions. | Not precise for non-integer solutions. |
Task 3
Solve for linear equation 3x + 2 = 11 and show value of x?
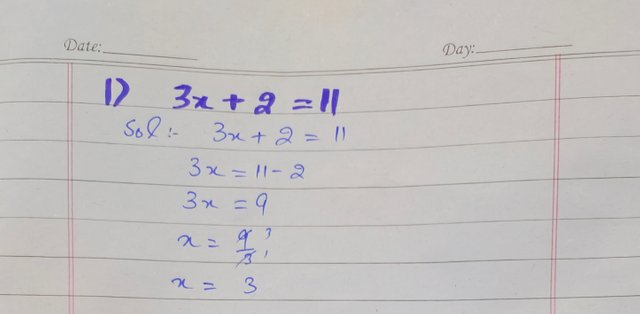 |
|---|
Solve for this quadratic equation x^2 + 2x - 6 = 0.
 |
|---|
Task 4
Scenario 1: Solving for the Remaining Money
Problem:
Ali has $15 for snacks and spends $3 on a pack of chips. The equation is:
x + 3 = 15
where x is the money Ali has left.
Step-by-Step Solution:
Start with the given equation:
x + 3 = 15
Subtract 3 from both sides to isolate ( x ):
x = 15 - 3
Simplify:
x = 12
Ali has $12 left after buying the pack of chips.
Scenario 2: Maximum Height Reached by the Ball
 |
|---|
The ball reaches a maximum height of 20 meters after 2 seconds.
kind Regards
@artist1111

Adieu, folks!
May the winds of fortune
carry you to greatness!
May the winds of fortune
carry you to greatness!