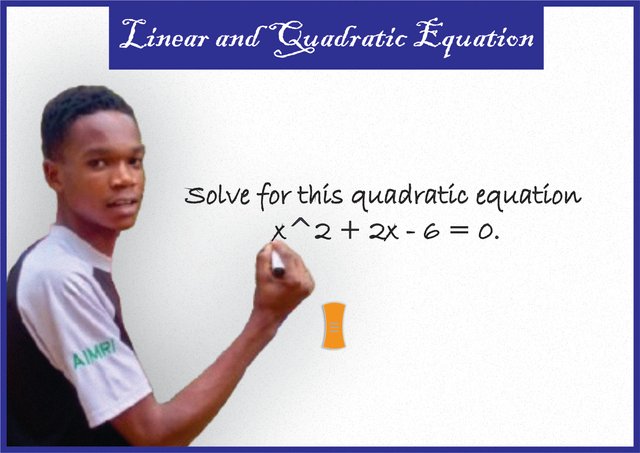
Here I'm going to provide detailed solutions to the homework tasks using the knowledge and examples from the class, I'm going to be detailed and work straight to the point and a brief and understandable examples.
| Task | 1: |
Explain difference between linear and quadratic equations. Provide examples of each type of system of equation and describe their general forms
Answer...
Linear equations are equations where the highest power of the variable is 1 as was explain in the class an algebraic example to best describe this is 2x + 3 = 5
A real life practical example is the bakery salers in a shop selling 250 loaves of bread each day and making a profit of N100 per loaf and still will to increase their profit from N25,000 to N30,00 to maximize their profit.
While
Quadratic equations are equations where the highest power of the variable is 2, an algebraic example to explain is
X^2 + 4X + 4= 0
A real life practical example to explain it better is the trajectory of a ball thrown upward from the ground with an initial velocity of 20 meters per second
| Task | 2: |
Describe methods for solving quadratic equations and share pros and cons for each method.
Answer...
Quadratic equation do not have only one method to solve it problem, it rather have different way to arrive at the satisfiying solution, There are three methods for solving quadratic equations.
Let's explore below...
Factoring Method: in this method it involves factoring the quadratic equation into two binomials which set each binomial equal to 0, and then solving for x
Example
x^2 + 5x + 6 = 0
Factoring
(x + 2)(x + 3) = 0
Solving
x + 2 = 0 or x + 3 = 0
x = -2 or x = -3
Pros: the advantage of using this method is that is simple and straightforward making it a good option when choose methods.
Cons: it has a disadvantage of being limited to special cases.
Quadratic Formula Methods :
in this method it have to do with the involvement of usiing the quadratic formula x = ( - b + √ ( b^2 - 4ac )) / 2a to solve it quadratic equation
Example
X^2 + 4x + 4 = 0
a = 1, b = 4, c = 4
x = ( -(4) ± √((4)^2 - 4(1) (4))) / 2(1)
x = ( -4 ± √(16 - 16 )) / 2
x = -2
Pros: the advantage of this method is that it works for all cases making it one of the best method to use.
Cons: Can be complex and difficult to remember.
Graphing Method : in this method have to do with thee involvemment of graphing the quadratic equation on a co ordinate plane and find the x intercepts
Example
x ^2 + 2x - 3 = 0
Graph
Here it done by crosses the x axis at x = -3 and x = 1.
Pros: an advantage of the method is that it visual represent the problems and solution.
Cons: here is disadvantage of graphing method, it may in some situation not provide exact solutions to the problem.
| Task | 3: |
Solve for linear equation 3x + 2 = 11 and show value of x?
Solve for this quadratic equation x^2 + 2x - 6 = 0
Answer...
To solve the two equations in this task the following steps are to be taken to achieve
Solving for Linear Equation ➡️ 3x + 2 = 11
Understanding the equation by isolate the variable x
Using the addition method to subtract 2 from both sides
- Now, I'm solving for x by dividing both sides by 3 to get x = 3 as my answer.

Solving for Quadratic Equation ➡️ X^2+2x - 6 =0
Understand the equation by recognize it as a quadratic equation
Using the factoring method to factorize the equation into (x + 3)( x - 2) = 0
Solving for x by set each factor equal to 0 and solve for x to arrive at my answer x = -3 or x = 2

| Task | 4: |
Scenario number 1
Suppose Ali have $15 for spending at snacks. He is buying a pack of chips for $3. How much money he have left?
Suppose x is amount of money Ali has left.
Equation: x + 3 = 15
Share a solution for x
(Solve the above scenerio based questions and share step by step that how you reach to your final outcome)
Scenario number 2
Suppose there's a ball which is thrown in upward direction from ground with initial velocity of 20 m/s and height of ball above ground is presented by following equation;
h(t) = -5t^2 + 20t
Here h is height in meters and t is time in seconds.
Share about maximum height reached by this ball!
Please solve for h!
Answer...
Before I could solve these two scenarios in this Task 4 the following steps was taken to achieve that.
Scenario 1
Ali's Snack Money
Understand the problem as Ali had $15 to spend on snacks and buys a pack of chips at $3 rate
Seting up the equation by x + 3 = 15 where x is the amount of money Ali has left in his hand
Solving the equation using the addition method by subtracting 3 from both sides to arrive at x = 12
Scenario 2
Maximum Height of the Ball
Understanding the problem as a ball is thrown upward with the initial velocity of 20 m/s and its height is given by the equation h(t) = -5t^2 + 20t
Identifing the type of equation which is the quadratic equation
Finding the vertex of the parabola to determine the maximum height, happened through using the formula t = -b / 2a to find the time at which the maximum height is reached
Substituting the time into the equation to find the maximum height where is follows h(2) = -5(2)^2 + 20(2) = 20 meters.
Equation :
x + 3 = 15
Using the Addition Method
x + 3 = 15
Subtract 3 from both sides
x = 12
Now, Ali has $12 left.
Scenario 2: Maximum Height of the Ball
Equation :
h(t) = - 5t^2 + 20 t
Now to find the maximum height we need to find the vertex of the parabola
Vertex : t = -b / 2a
Substituting the values we get
t = - 20 / (2 * -5)
t = 2
Substitutting t = 2 into the equation
h(2) = -5(2)^2 + 20(2)
h(2) = -20 + 40
h(2) = 20
Finally arriving at the answer, the maximum height reached by the ball is 20 meters.
Thank you all for learning me, love you all.

