Dear Steemian friends,
At first, take my cordial salam. This is @nahiansajid from #bangladesh. It's hoped that all of you are well by the grace of omni-merciful ALLAH. I am also great by the grace of almighty ALLAH. Today, I'm going to take part in "SLC-S22W4//Linear and Quadratic equations equations".

Explain difference between linear and quadratic equations. Provide examples of each type of system of equation and describe their general forms.
- Definition of Linear Equation :-
A linear equation is an algebraic equation in which the highest power of the variable(s) is 1. It represents a straight line when plotted on a graph.
- Definition of Quadratic Equation :-
A quadratic equation is an algebraic equation in which the highest power of the variable is 2. It represents a parabola when plotted on a graph.
Difference between Linear Equation and Quadratic Equation :-
| Feature | Linear Equation | Quadratic Equation |
|---|---|---|
| Definition | An equation where the highest power of the variable is 1. | An equation where the highest power of the variable is 2. |
| General Form | ax + by = 1 (single variable) or, ax + by + c = 0 (two variables) | ax^2 + bx + c = 0, where a is equal not 0 |
| Graph | It represents a straight line in 2D space. | It represents a parabola in 2D space. |
| Solutions | Linear equations have a single solution, but in some case, it can have no solution (parallel lines) or infinitely many (in systems) | Quadratic equation can have two, one, or no real solutions, depending on the discriminant (b^2 - 4ac) |
Examples of Systems of Equation
- Linear System Example :
- x + y = 6
- x - y = 2
This system can be solved to find x = 4 and y = 2
- Quadratic System Example :
- y = x^2 + 3x + 2
- y = 2x + 1
These equations intersect at two points. This system can be solved to find
x = -3, y = -5
and
x = -1, y = -1 .
General Froms
- General forms of linear equation :
The general form of linear equation in one variable is:
ax + b = c
a is not equal 0
a, b and c are real numbers.
The general form of quadratic equation is :
az^2 + bx + c = 0
a is not equal 0
b is the coefficient of x
c is a constant

Describe methods for solving quadratic equations and share pros and cons for each method.
There are several methods for solving quadratic equations. I'm going to share the common methods.
1. Factoring
- Process :-
First of all, we have to express the quadratic equation as two binomials, like,
ax^2 + bx + c =0, and it can be solved factoring into (px + q)(rx + s) = 0, then, we can easily find out the value of x.
- Pros :-
When it works, it's simple to solve and it provides the roots quickly.
- Cons :-
The main demerit is that it doesn't always work because all equations can not be factored. Sometimes, it becomes so complex to get the equation factored.
2. Quadratic Formula
- Process :-
The general solution for a quadratic equation is given by :-
x = (-b ± √(b^2 - 4ac))/2a
- Pros :-
In this method, there doesn't matter whether the quadratic equation is factorable or not factorable.
- Cons :-
Sometimes, it provides complex solutions if the discriminant is negative. It needs to remember the formula. Some teachers don't prefer it when the equation can be solved through factoring method.
3. Graphing
- Process :-
It needs to graph the quadratic function,
y = ax^2 + bx + c, then, we can easily find out the value of x where it crosses the x-axis.
- Pros :-
It is visible method, and helpful in understanding the behaviour of quadratic function.
- Cons :-
This method may not be effective for large values. It needs graph paper or external software.

Step by step process to solve the linear equation (3x + 2 = 11) is following :-
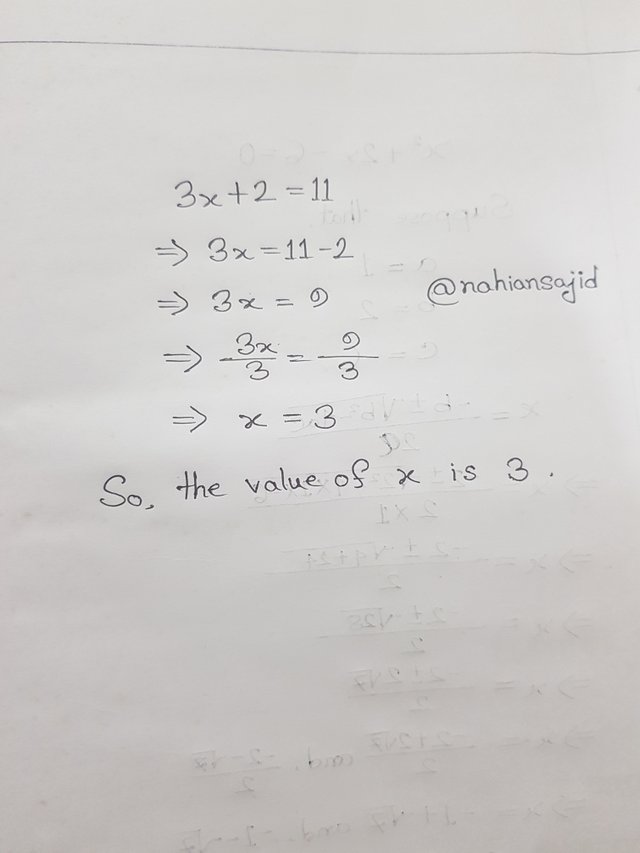
Step by step process to solve the quadratic equation (x^2 + 2x - 6 = 0) is following :-
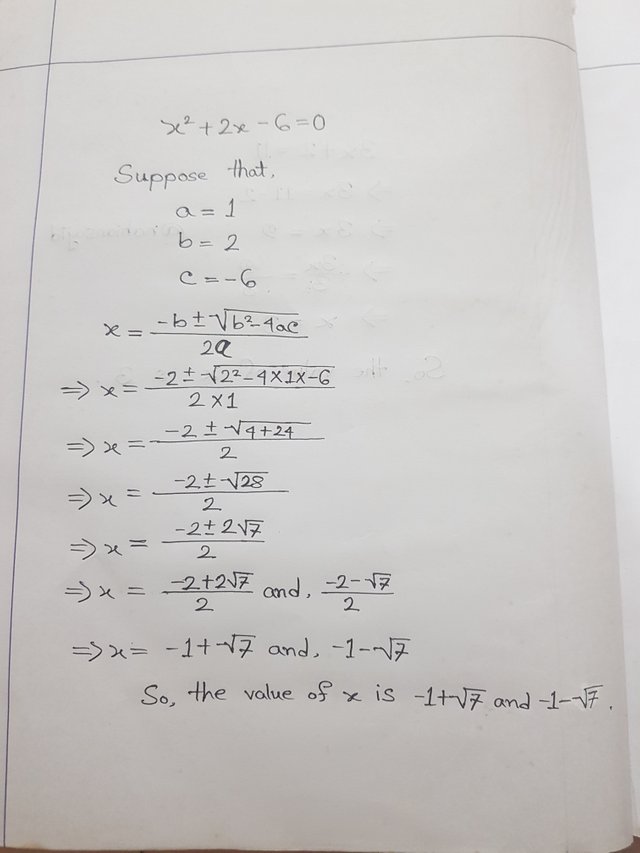

Solution for the real life scenario number 1:
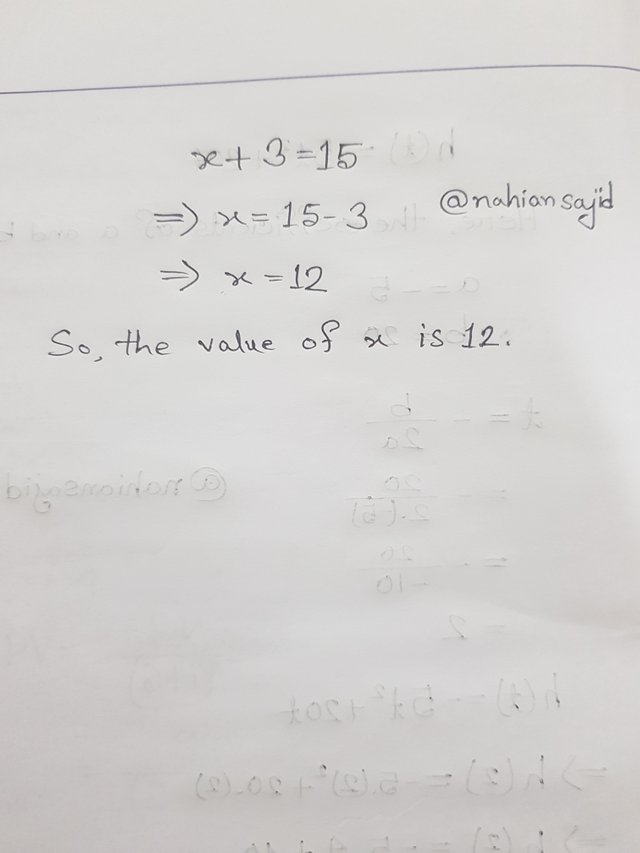
Given Equation
x + 3 = 15
x = 15 - 3
x = 12
So, the value of x is 12. It means, Ali has left 12$.
Solution for real life scenario number 2

Given Equation
h(t) = -5t^2 + 20t
We have to find out the maximum height (h). So, at first, we have to identify the value of t when the ball reaches at the maximum height.
We have to use the formula for the vertex of parabola.
t = -b / 2a
Here, a = -5 and b = 20
t = -20 / 2×(-5)
t = -20 / -10
t = 2
So, the value of t is 2 seconds.
Now, we can easily find out the maximum height.
h(t) = -5t^2 + 20t
h(2) = -5×(2)^2 + 20×(2)
h(2) = -5×4 + 40
h(2) = -20 + 40
h(2) = 20
So the maximum height that the ball can reach is 20 meters.

| No | My invited steemit friends |
|---|---|
| 1 | @kalidsyfulla |
| 2 | @mdpolasmia |
| 3 | @mahadisalim |
