Assalamualaikum everyone!
Welcome back to my blog. The topic of discussion for today is Linear and Quadratic Equations arranged by @khursheedanwar. So, let's start the fun without any wastage of time.
Task 1
- Def:
We can define a linear equation as, it is an algebraic equation in which the highest power of the variable is 1. Linear equations are fundamental expressions in algebra and are used to determine and find the relationships with a constant rate of change.
- General Formula:
A linear equation can be written as:
Here,
( a ) is the coefficient of the variable ( x ).
( b ) is the constant term.
This eq. is linear only if a is not equals to 0. If a = 0, then it will not be a linear eq.
- Examples:
Algebraic Example: 3x−7=8
Solution: Add 7 to both sides: 3x=15. Divide by 3: x=5.
Practical Example:
A car rental company charges a flat fee of $20 plus $0.10 per mile driven. If a customer’s total bill is $50, how many miles (x) did they drive?
Equation of this scenario will be: 20+0.10x=50
Solution: Subtract 20: 0.10x=30. Divide by 0.10: x=300 miles
- Def:
It can simply be defined as a quadratic equation is a polynomial equation where the highest power of the variable is 2. Quadratic equations are often used to model or determine the situations with a changing rate of change, such as projectile motion, etc.
- General Form
A quadratic equation is written as:
Here,
( a ), ( b ), and ( c ) are constants.
This eq. will be quadratic only if a is not equals to 0, if ( a = 0 ), then the equation becomes linear.
- Examples:
Algebaric Example: 2x^2 −3x−5=0
Solution: We will use factoring, quadratic formula, or graphing. I'll discuss these methods in the next parts of this post.
Practical Example:
A toy company designs a rectangular box for the package of their product. The box needs to have a fixed volume of 500 cubic centimeters. The length of the box is 10 cm longer than its width, and the height is 5 cm. If the width of the box is (x) cm, the relationship between the dimensions can be modeled by the quadratic equation:
x (10+x) (5) = 500
This equation can be solved to determine the width of the box.
| Aspect | Linear Equations | Quadratic Equations |
|---|---|---|
| Highest Power | 1 | 2 |
| Graph | Straight line | Parabola |
| Solutions | One solution | Zero, one, or two solutions |
| Rate of Change | Constant | Changes over time |
| Example | 3x−7=8 | 2x^2 −3x − 5=0 |
Task 2
There are basically three major methods to solve a quadractic equation. Below is the explanation of each method with examples.
- Description:
The factoring of the quadractic eq. involves expressing the quadratic equation as a product of two binomials. This method works only when the quadratic equation is factorable into integers.
- Example:
Solve the equation, x^2 + 7x + 10 = 0.
Factoring: (x+5)(x+2)=0.
Solutions: x=−5,x=−2.
- Pros
This method is simple and quick, if factors are easy to find.
It doesn’t require any form of complex calculations.
- Cons:
This method only works if the quadratic equation is easily factorable.
- Description:
It is also known as the universal method to solve the quadratic equations. The quadratic formula provides an exact solution for any quadratic equation. It is derived from completing the square.
- Formula:

(-b ± √(b^2 - 4ac)) / 2a
Steps:
- Write the equation in standard form.
- Identify ( a ), ( b ), and ( c ).
- Substitute the values into the formula and simplify it.
Example:
Solve, 3x^2 +6x −9 = 0.
Here, a = 3, b = 6 and c = −9.
So, it can be plugged into the quadratic eq, as;
x = (-(6) ± √((6)^2 - 4(3)(-9))) / 2(3)
x = (-6 ± √(36 + 108)) / 6
x = (-6 ± √(144)) / 6
x = (-6 ± 12)) / 6
| x = (-6 + 12) / 6 | x = (-6 - 12) / 6 |
|---|---|
| x = 1 | x = -3 |
So, we have the values of x which are, -3 and 1
- Pros:
This method always works for any quadratic equation.
It handles equations with complex or irrational solutions.
- Cons:
It can be computationally intensive for large coefficients.
It requires careful calculations to avoid errors.
- Description:
This method involves graphing the quadratic equation ( y = ax^2 + bx + c ) on a coordinate plane. The ( x )-intercepts (if they exist) are the solutions.
Steps:
- First of all, rewrite the equation in standard form.
- Then, plot the graph using a table of values or graphing software.
- Identify the points where the parabola crosses the ( x )-axis (these are the solutions).
Example:
Solve, ( x^2 - 4x + 3 = 0 ).
Have a look at the graph for this equation,
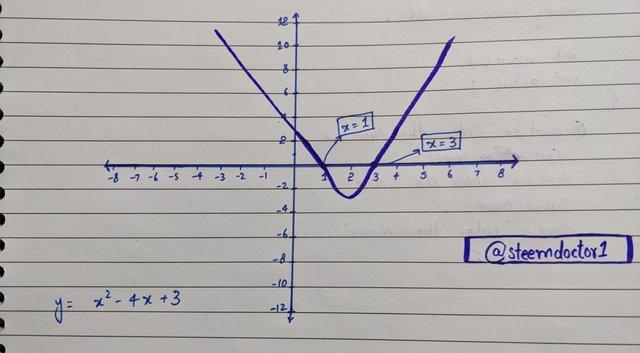
It can be clearly seen that the parabola line intersects the x-axis at x=1 and x=3 which are the roots of the equation.
- Pros:
This method provides a visual representation of the equation.
Thismethod is helpful for understanding the behavior of the quadratic function.
- Cons:
It requires graphing tools or software.
It may not provide precise solutions, especially for non-integer values.
| Method | Pros | Cons |
|---|---|---|
| Factoring | Simple and very easy for small coefficients. | Limited to equations that can be factored easily. |
| Quadratic Formula | Always works and handles complex solutions. | Lengthy calculations are susciptible to errors. |
| Graphing | Provides a clear visual understanding. | Precision of the results depends on graphing accuracy. |
Task 3
- Solve for linear equation 3x + 2 = 11 and show value of x?

The equation 3x+2=11 can be solved algebraically:
Subtract 2 from both sides, we have:
3x=9
Divide both sides by 3:
x=3
So, we have the answer which is x=3.
- Solve for this quadratic equation x^2 + 2x - 6 = 0.
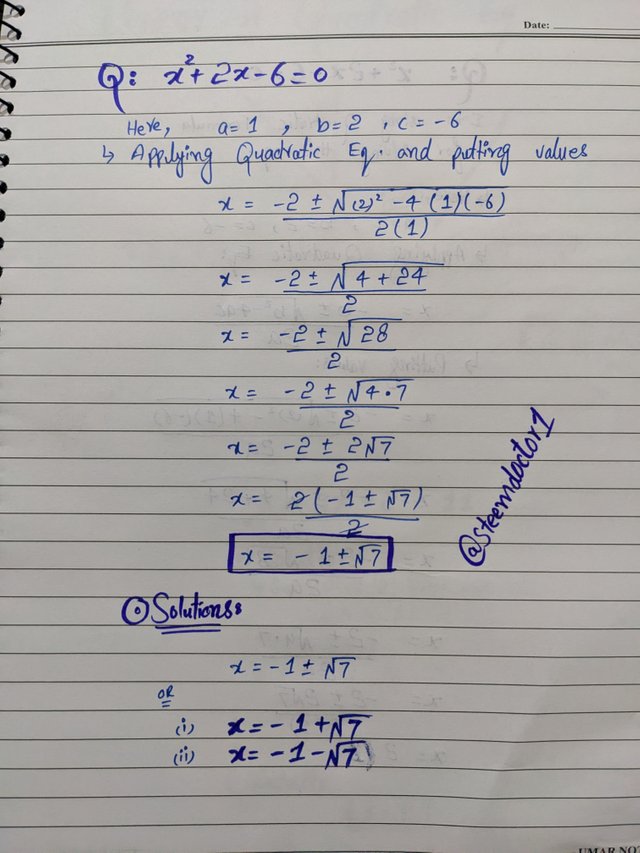
I have used the quadratic formula method to solve this equation. The reason is quite simple that the mid-term of this equation was not easy to break as there were no factors which can satisfy the results, that's why using quadratic equation is preferable.
The answers are,
x = -1 + √7 ≈ 1.65
And,
x = -1 - √7 ≈ -3.65
This equation can also be solved by using the graphical method. As shown,
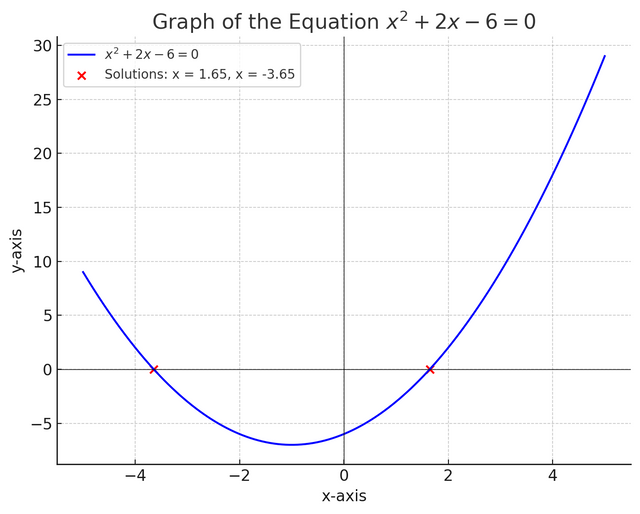
Task 4
- Scenario Number 1:
We are given:
Ali has $15 to spend on snacks.
He buys a pack of chips for $3.
We need to find how much money Ali has left (denoted as x). The equation is provided: x+3=15
First of all, we have to understand the equation. The equation states that Ali has an amount of money left (represented by x), after he spends $3.
Now, solve for x:
Subtract 3 from both sides of the equation:
x = 15 − 3
Now, simplify the expression,
x = 12
Final Outcome:
Ali has $12 left after buying the pack of chips.
- Scenario 2:
We are given:
The height of the ball above the ground is represented by the equation:
h (t) = −5 t^2 +20t
h(t) is the height in meters and t is the time in seconds.
The ball is thrown upward with an initial velocity of 20 m/s.
First of all, we will identify the quadratic equation.
The equation is of the form:
h (t) = −5 t^2 + 20t
This represents a parabolic trajectory, and the maximum height corresponds to the vertex of the parabola.
But, first we have to find the time at which the maximum height occurs.
For a quadratic equation of the form;
ax^2 + bx + c = 0 , the time at which the maximum height occurs is given by the formula:
t = -b/2a
Here,
a =−5 and b=20.
Substituting these values:
t = -20 / 2 (-5)
t = -20 / -10
t = 2
So, the maximum height occurs at, t = 2 seconds.
Now, we can easily find the maximum height by substituting t=2 into the height equation.
h(t)=−5t^2 + 20t
Putting Values,
h(2) = −5(2)^2 + 20 (2)
h(2) = −5(4) + 40
h(2)=−20+40 = 20
Final Outcome:
The maximum height the ball reaches is 20 meters.
 |  |  |  |
|---|

