"SLC-S22W5//Polynomial and rational expressions."

• Task 1

• Explain difference between polynomial and rational expressions .Provide examples of each type of system of equation and describe their general forms.

Polynomial and Rational Expressions

• Polynomial Expressions: These are those that combine numbers, variables and basic arithmetic operations (addition, subtraction, multiplication and exponentiation), where the exponents of the variables are always non-negative whole numbers, although normally decimal or fractional numbers can also accompany the variables.

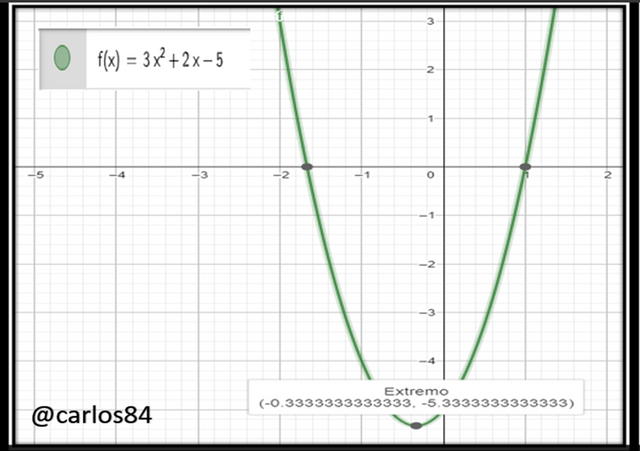
  • Example: 3x² + 2x - 5

Although we can call the above expression a second degree equation, it still meets the characteristics that define a polynomial, so it can be called a second degree equation or second degree polynomial.

A polynomial, regardless of its degree, can be expressed as a function f(x), i.e. as a polynomial function, example: f(x)= 3x² + 2x - 5, let's see its graph:

• General form: aₙxⁿ + aₙ₋₁xⁿ⁻¹ + ... + a₁x + a₀, where the coefficients aₙ, aₙ₋₁, ..., a₁, a₀ are real numbers and n is a non-negative integer.

• Rational Expressions: They are the quotient of two polynomials. That is, they are algebraic fractions where both the numerator and the denominator are polynomials.

  • Example: (2x² + 1) / (x - 3)

We can notice how in the previous example the division or quotient of two polynomials generates a rational polynomial.

Similarly rational polynomials can also be expressed as a function f(x), the only thing is that there are elements of a rational function that can only be understood with infinitesimal calculus, with concepts of limit of a function and derivative of a real function, since for any value of x where the denominator becomes zero can be a vertical asymptote, but that I imagine I will be understood by Professor @khursheedanwar in later challenges.

An example might be f(x) = (2x² + 1) / (x - 3), which can be graphed as:

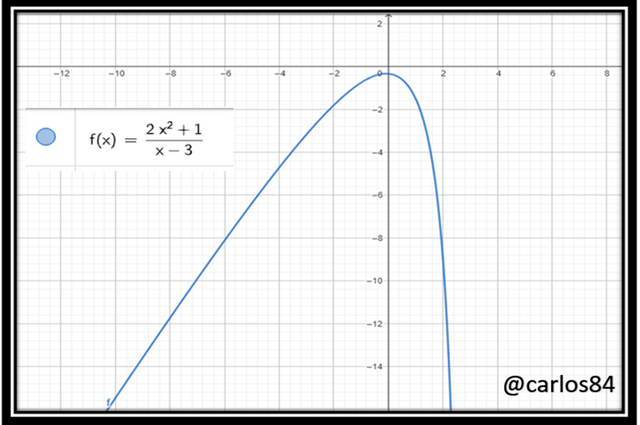
As can be seen in the graph, the curve sticks to the straight line x= 3, which means that x = 3 is a vertical asymptote, however it is by calculating the existence of the following limit that we can corroborate the veracity of the vertical asymptote:

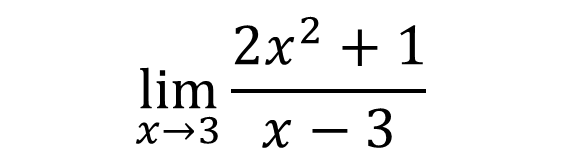
I do not want to explain how the limit of the rational function is solved because it is not the subject of discussion, however the existence of the limit makes us conclude that it is a false vertical asymptote at x=3, in the case that the limit does not exist means that x=3 is a vertical asymptote.

General form: P(x) / Q(x), donde P(x) and Q(x) are polynomials and Q(x) ≠ 0.

As I mentioned earlier, the polynomial of the denominator must be non-zero, since division by zero is not defined.

Systems of Equations with Polynomial and Rational Expressions

A system of equations is a set of two or more equations that must be satisfied simultaneously.

• Systems of Polynomial Equations:
  • Example:
    2x + y = 5
    x² - y = 1

It should be noted that in a system of polynomial equations the equations can be of different degrees, quadratic, linear, cubic, among others.

General form:

a₁₁x + a₁₂y = b₁
a₂₁x + a₂₂y = b₂

These systems are usually solved by methods such as substitution, equalization or reduction. However, depending on the degree of the polynomial it is decided which method can be used to solve the system of equations.

• Systems of Rational Equations:

• Example:
  1/x + 1/y = 3
  x - 2y = 1

  • General form:
    P₁(x,y) / Q₁(x,y) = R₁(x,y)
    P₂(x,y) / Q₂(x,y) = R₂(x,y)

These systems can be more complex to solve and often require additional techniques such as denominator elimination or factoring.

Differences

Feature	Polynomial Expressions	Rational Expressions
Structure	Sum of terms with non-negative integer exponents	Quotient of two polynomials
Graph	Generally straight lines or smooth curves	They can have asymptotes and discontinuities.
System resolution	More direct algebraic methods	May require more advanced techniques

Applications:

• Polynomials: They are used in a wide variety of fields, from physics and engineering to economics and computer science. For example, to model projectile trajectories, describe population growth or fit data to curves.

• Rational Expressions: They are used in optimization problems, electrical circuit analysis, concentration calculations and in many other areas of science and engineering.

In Conclusion

Polynomial and rational expressions are fundamental tools in algebra and are used to model a wide variety of phenomena.

Systems of equations involving these expressions are solved using different techniques, depending on their complexity.

As a petroleum engineer I consider that the two forms of algebraic expressions are very important, since the two forms of expressions can be expressed in the form of functions and can model much of the flow behavior of a reservoir or oil well, you can also model the behavior of a well according to its production capacity and where variables such as temperature, volume and pressure influence.

One of the most striking differences between these two types of algebraic expressions such as polynomials and rational expressions, is that the polynomials of first degree, second degree, third degree and so on as the degree increases, are polynomials whose functions have no restrictions, are easy to graph and have no discontinuity, while rational functions have vertical or oblique asymptotes, and have restrictions in their domain, and can only be studied with infinitesimal calculus, either by solving a limit or a derivative.

• Task 2

Explain steps used in simplifying a rational expression.Write some common factors required to be cancel out?

Factorize numerator and/or denominator: Look for common factors in both parts of the fraction. This involves decomposing polynomials into products of simpler factors. It may be the case where only the numerator or only the denominator needs to be factored, as it may be the case where the numerator or denominator is already factored.

Example:

(x² - 4) / (x + 2).

The numerator is a difference of squares, so it is factored as (x + 2)(x - 2). The denominator is already factored.

So the (x + 2) terms cancel, leaving only the expression: 1 / (x - 2).

Identify common factors: Once factored, find the factors that appear in both the numerator and denominator.

As explained above, the factors that are identified as common in both the numerator and denominator are (x+2)

Cancel the common factors: Eliminate the common factors from the numerator and denominator. Remember that any number divided by itself equals 1.

The term that cancels in the numerator and denominator is (x+2).

Write the simplified expression: The resulting expression will be the simplified rational expression.

(x² - 4) / (x + 2) = (x+2)(x-2) / (x+2) = 1 / (x-2)

Factor both the numerator and denominator: Look for common factors in both parts of the fraction. This involves decomposing polynomials into products of simpler factors.

Example: (x² - 4) / (x + 2).

Identify common factors: Once factored, look for factors that appear in both the numerator and denominator.

(x-2)(x+2) / (x+2)

The common factors are (x+2) in the numerator and (x+2) in the denominator.

Cancel the common factors: Eliminates the common factors from the numerator and denominator.
It eliminates x + 2 in the numerator and denominator.

Write the simplified expression: The resulting expression will be the simplified rational expression.

(x-2)(x+2) / (x+2) = (x-2) / 1 = x-2

Common factors commonly encountered:* * Monomics: A term consisting of a number and one or more variables raised to a non-negative integer power (e.g., 2x, 3y², 5.

• Monomics: A term consisting of a number and one or more variables raised to a non-negative integer power (e.g., 2x, 3y², 5).
• Binomials: Algebraic expressions with two terms (e.g., x + 2, 3y - 5).
• Trinomials: Algebraic expressions with three terms (e.g., x² + 5x + 6).
• Difference of squares: A binomial of the form a² - b² that is factored as (a + b)(a - b).
• Perfect square trinomial: A trinomial of the form a² + 2ab + b² or a² - 2ab + b² that factors as (a + b)² or (a - b)².

Another example:.

Simplify: (6x² + 9x) / (3x)

• Factorize: We take out common factor 3x in the numerator: 3x(2x + 3) / 3x
• Cancel: We cancel the common factor 3x.
• Simplify: The simplified expression is 2x + 3.

It is good to emphasize that the domain of the rational expression must be verified, i.e. the values of x that make the denominator zero must be excluded from the domain. When graphing, the value of x where the denominator becomes can be a vertical asymptote.

Factorization is key, so being able to master factorization techniques will allow us to simplify any rational expression.

• Task 3

Please add these polynomial expressions 3x^2 + 2x + 1 and 2x^2 - x - 3 and share your final expression.

Share multiplication of polynomial expressions 2x + 3 and x - 2 with final outcome of resulting expression.

(You are required to solve these problems at paper and then share clear photographs for adding a touch of your creativity and personal effort which should be marked with your username)

Of the resulting polynomial of second degree its graph is:

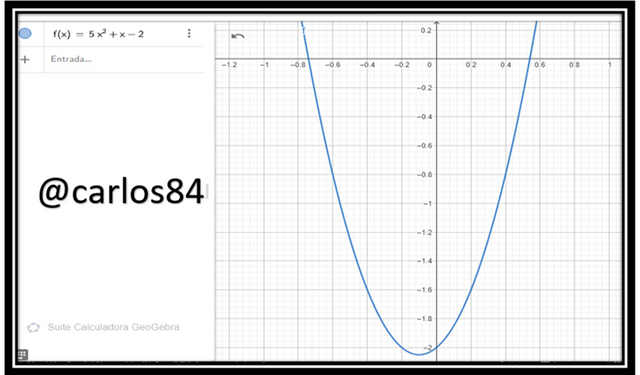
Of the polynomial resulting from the multiplication of the two polynomials of first degree that is a polynomial of second degree, its graph is:

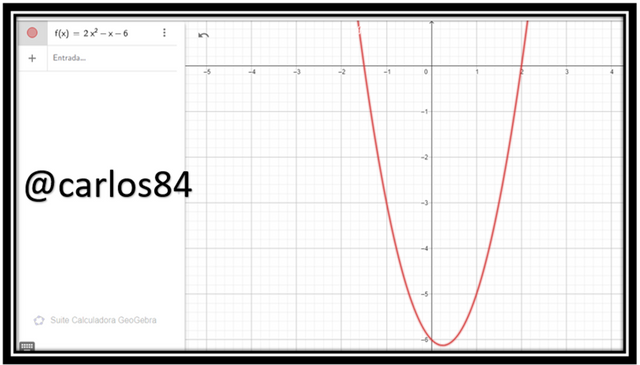
Considerations: If we add or subtract polynomials of the same degree, just as we added algebraically the two second degree polynomials, the resulting polynomial is going to be of the same degree, in this case of second degree. When we multiply two polynomials of first degree the two polynomials, the resulting polynomial is a polynomial of second degree, as expressed in the example of task 3.

• Task 4

Scenario number 1

Suppose if there's a person named Ali have craft store and he is selling beads in x packet which have fixed cost of $5 plus $2 for each packet.Now you have to write polynomial expression for representing total cost(C)of buying for x packets of beads by considering that there's a 10% discount+Also you have for calculating total cost of Ali buys 5 packets of beads.

(Solve the above scenerio based questions and share step by step that how you reach to your final outcome)

Understanding the problem:

• Ali sells in packs of x units.

• Each package has a fixed cost of $5 plus an additional $2 per package.
  Therefore in equation form it would be: 5 + 2x

• There is a 10% discount on the total price (10% = 0.1).

• We want to find an expression for the total cost (C) as a function of x and then calculate the cost for 5 packages.

Therefore the expression for the total cost as a function of x packages is:

C(x) = (5 + 2x) - 0.1(5+2x).
C(x) = 5 + 2x - 0.5 - 0.2x
C(x) = 4.5 + 1.8x

Therefore the total cost function C(x) = 4.5 + 1.8x

So the total cost when x = 5 packages is equal to:

C(5) = 4.5 + 1.8 (5)
C(5) = 4.5 + 9
C(5) = $13.5.

Considerations: We could consider two cost functions, one without discount, or one with discount:

C(x) = 5 + 2x (without discount).
C(x) = 4.5 + 1.8x (with 10% discount)

When Ali buys 5 packages without discount it would make a total cost of 5 + 2(5) = $15.
When Ali buys 5 packages with 10% discount it would make a total cost of 4.5 + 1.8 (5) = $13.5.

If we want to plot the cost function C(x) without discount:

C(x) = 5 + 2x

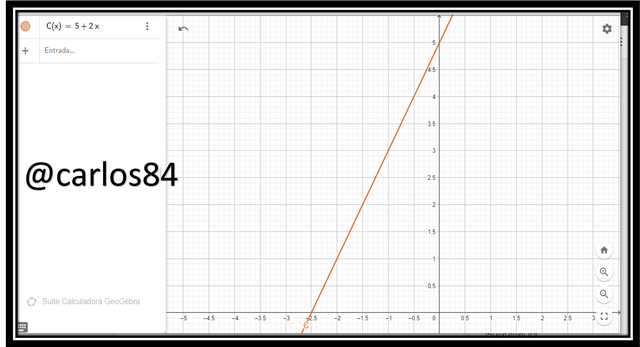
When x = 5 packages:

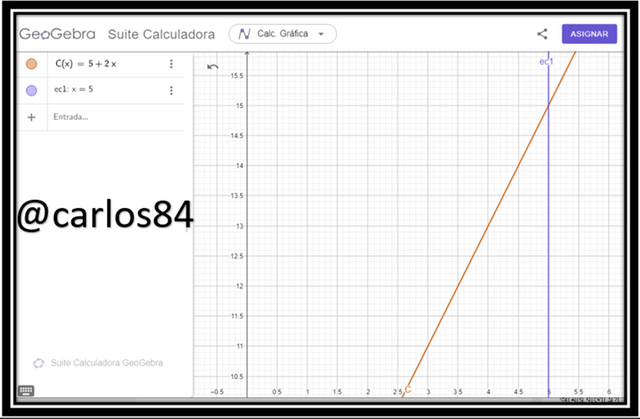
In the graph above we can see that when the line x=5 is intercepted with the line C(x) = 5 +2x it gives a total cost of 15 dollars.

This means that when Ali buys 5 packages without discount she has a cost of $15.

When the function C(x) is 10% off, C(x) = 4.5 + 1.8x.

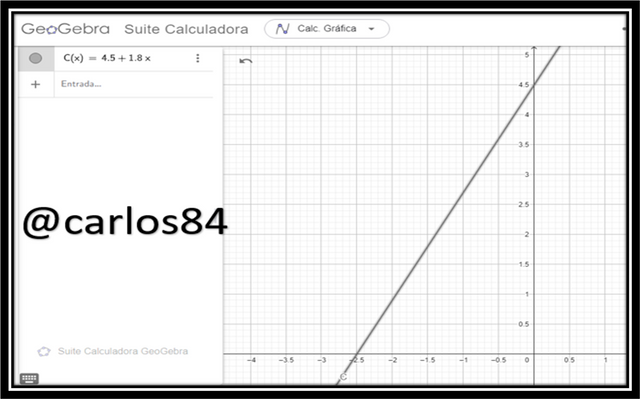
If X = 5 packages:

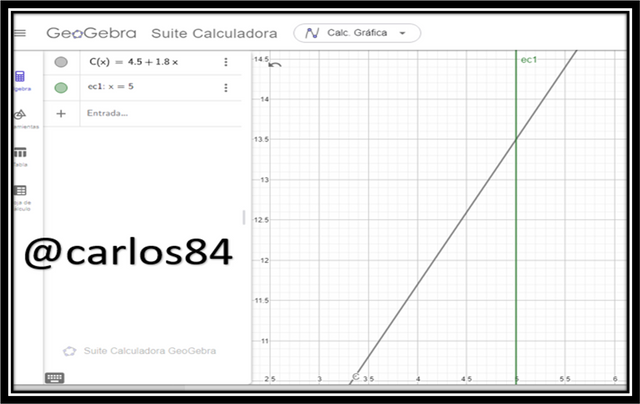
In the previous graph we can see that when the line x=5 is intercepted with the line C(x)= 4.5 + 1.8x it gives a total cost of 13.5 dollars.

This means that when Ali buys 5 packages with a 10% discount she has a cost of 13.5 dollars.

Scenario number 2

Suppose there's a farmer harvesting x tons of wheat and 3x tons of barley.Now you need to write a rational expression for representing ratio of wheat to total harvest in which there's wheat and barley and you have to simplify expression also at end+You also need for calculating ratio of wheat to total harvest if farmer is harvesting 4 tons of wheat.

Understanding the problem:

• The farmer harvests x tons of wheat.

• The farmer harvests 3x tons of barley.

• We want to find the ratio of wheat to total harvest.

• Calculating the total harvest:

Total harvest is the sum of wheat and barley:

Total harvest = wheat + barley.

Total harvest = x + 3x

Total harvest = 4x

Calculating the ratio of wheat to total harvest:

The ratio can be expressed as a fraction:

Ratio = (quantity of wheat) / (total harvest).

Ratio = x / 4x

Simplifying the expression:

We can simplify the fraction by dividing both the numerator and denominator by x:

Ratio = (x / x) / (4x / x)

Ratio = 1 / 4

Conclusion: The rational expression representing the ratio of wheat to the total crop is 1/4.

This means that wheat represents a quarter or 25% of the total crop, regardless of the exact amount of wheat harvested.

Calculating the ratio for 4 tons of wheat:

If the farmer harvests 4 tons of wheat, the ratio will remain the same, since the ratio is a constant proportion and does not depend on the specific amount of wheat. Therefore, the ratio of wheat to total crop will remain 1/4.

The ratio of wheat to total crop is always 1/4, which means that wheat represents one-fourth of the total crop, regardless of the amount of wheat harvested.

This ratio is constant and does not change as the amount of wheat harvested varies.

Conclusion: No matter how many tons of wheat the farmer may harvest, wheat will always represent one-fourth of his total crop, as long as the ratio of wheat to barley remains 1:3.