Saludos amigos steemians.

Explicar la diferencia entre expresiones polinómicas y racionales. Proporcionar ejemplos de cada tipo de sistema de ecuaciones y describir sus formas generales.
Las Expresiones Polinómicas, son expresiones algebraicas que se componen de variables, operaciones aritméticas (+, -, ×) así como coeficientes en la que el índice es una potencia entera positiva. Se caracterizan:
- Contienen variables que podrían ser cualquier letra del alfabeto.
- Los coeficientes que son constantes por las cuales se multiplican las variables.
- Las potencias o índices que son números enteros positivos que indican el exponente al que se eleva la variable.
- Cada términoe está separada por operaciones aritméticas que son las operaciones básicas en matemáticas, incluyendo la suma, la multiplicación y la resta.
Las expresiones polinómicas se pueden clasificar en monomios, binomios, trinomios y polinomios según el número de términos que contengan.
La forma general de la expresión polinómica es la siguiente:mx² + ny - o
Donde x e y son variables, m y n son coeficientes y constantes, y o también es una constante. Se puede observar que la potencia en la expresión dada es un entero positivo.
Los siguientes son ejemplos algebraicos de expresiones polinómicas:
3x³ - 2y + 6
x³ + 4x² - x + 5
Un ejemplo práctico de ello sería una empresa prepara hamburguesas y el coste de producción (C) depende del número de hamburguesas (X). El costo de producción se puede representar mediante la siguiente expresión polinómica:
C(x) = 3x² + 5x + 18
Donde 3x² representa el costo de los materiales, que aumentará con el número de hamburguesas preparadas de forma cuadrática, 5x representa el costo de la mano de obra, que se incrementará de forma lineal con el número de unidades producidas, y 18 es el costo fijo de producción.
Por otro lado, se tiene que las Expresiones Racionales son expresiones algebraicas fraccionarias, compuestas por expresiones polinómicas; es decir, fracciones en la que los numeradores y los denominadores son expresiones polinómicas. Se caracterizan por:
- Una fracción que tiene polinomios, tanto en el numerador como en el denominador.
- Contiene variables que están contenidas en los numeradores y denominadores de los polinomios.
La forma general de las expresiones racionales es: *a(x) / b(x). Donde x es la variable y a y b son el numerador y el denominador del polinomio, respectivamente.
Los siguientes son ejemplos algebraicos de expresiones racionales:
(3x² + 2x + 4) / (x² - 1)
(5y + 3) / (4 - y)
Un ejemplo práctico de ello seria una empresa que prepara hamburguesas y el coste de producción (C) depende del número de hamburguesas preparadas (X). La función de costo se puede representar mediante una expresión racional:
C(x) = (4y + 90) / (x + 2)
Donde 4x indica el costo variable de producción, 90 es el costo fijo de producción, x + 2 es el número total de hamburguesas producidas y 2 es el mínimo.
En síntesis, a continuación se representa un resumen de las principales diferencias entre lasiexpresiones polinómicas y expresiones racionales:
| Expresiones Polinómicas | Expresiones Racionales |
|---|---|
| Contiene términos con variables elevadas a un número positivo | Una fracción formada por 2 polinomios, uno en el numerador y otro en el denominador |
| El grado del polinomio es la mayor potencia de la variable | El grado depende tanto del numerador como del denominador. |
| Su gráfico es una curva suave | Su gráfico es una curva que puede tener asíntotas o agujeros verticales. |
| Se simplifica realizando agrupaciones de términos iguales | Se simplifica cancelando los factores comunes en la fracción. |
| Se puede sumar, dividir, multiplicar y restar. | Se puede sumar, multiplicar y restar; la división se puede realizar solo cuando el denominador no es cero. |
Explique los pasos utilizados para simplificar una expresión racional. Escriba algunos factores comunes que deben cancelarse.
Simplificar una expresión racional requiere cancelar los factores comunes tanto en el numerador como en el denominador.
Primeramente se deben factorizar el numerador y el denominador en sus distintos factores primos.
(2x² - 4xy) / (3x²y - 6xy²)
= (2x(x - 2y)) / (3xy(x - 2y)
Seguidamente, se identificar los factores comunes. En este caso el factor común en el numerador y denominador es: (x - 2y)
Ahora se procede a la cancelación de factores comunes, entre el numerador y el denominador:
(2x(x - 2y)) / (3xy(x - 2y)
= 2x / 3xy
Por último se procede a simplificar, lo que queda después de cancelar los factores comunes, siempre que sea posible.
2x / 3xy
= (2 (x)) / (3 (x)(y)) ===> por expansión x se cancelará
= 2 / 3y
Por lo tanto, (2x² - 4xy) / (3x²y - 6xy²) = 2 / 3y
Sume estas expresiones polinomiales 3x² + 2x + 1 y 2x² - x - 3 y comparta su expresión final.
Para sumar expresiones polinomicas, se deben seguir estos pasos:
- Ordenar los polinomios de mayor a menor.
- Completar con ceros los términos que faltan en algún grado.
- Agrupar los términos que tienen el mismo grado.
- Sumar los términos semejantes.
Los términos semejantes son aquellos que tienen las mismas variables y exponentes. Para sumar los términos semejantes, se suman los coeficientes, conservando el signo del coeficiente mayor. Veamoslo con el ejemplo planteado:
3x² + 2x + 1 y 2x² - x - 3
Aquí se puede observar que ambos términos se encuentran agrupados de forma decreciente, y no falta ningún grado, por tato no hay que rellenar con cero.
Se procede a agruipar los términos semejantes, es decir los que tienen el mismo grado.
(3x² + 2x²) + (2x - x) + (1 - 3)
Ahora, se realiza la suma de tales términos semejantes:
(3x² + 2x²) + (2x - x) + (1 - 3)
5x² + x - 2
A contiuación se muestran los cálculos que se han realizado para ello:

Compartir la multiplicación de expresiones polinómicas 2x + 3 y x - 2 con el resultado final de la expresión resultante.
Para multiplicar polinomios, se multiplica cada término de un polinomio por cada término del otro y luego se simplifican los términos semejantes. Para ello, deben seguirse los siguientes pasos:
- Multiplicar cada término del primer polinomio por todos los términos del segundo polinomio.
- Sumar los monomios que tienen el mismo grado.
- Simplificar los términos semejantes.
Para multiplicar polinomios se puede aplicar la propiedad distributiva, la cual establece que el término que está delante del paréntesis multiplica cada término dentro del paréntesis por separado. Veamoslo con el ejemplo planteado.
2x + 3 y x - 2
Se procede a aplicar la propiedad distributiva para multiplicar cada término de 2x + 3 por cada término de x - 2:
(2x + 3) * (x - 2)
= 2x(x - 2) + 3(x - 2)
Ahora se procede a realizar las multiplicaciones:
2x(x - 2)
= 2x² - 4x
3(x - 2)
= 3x - 6
Se combinan estos términos, y se procede a realizar las operaciones algebraicas correspondientes con los términos semejantes:
2x² - 4x + 3x - 6
2x² - x -6
A contiuación se muestran los cálculos que se han realizado para ello:
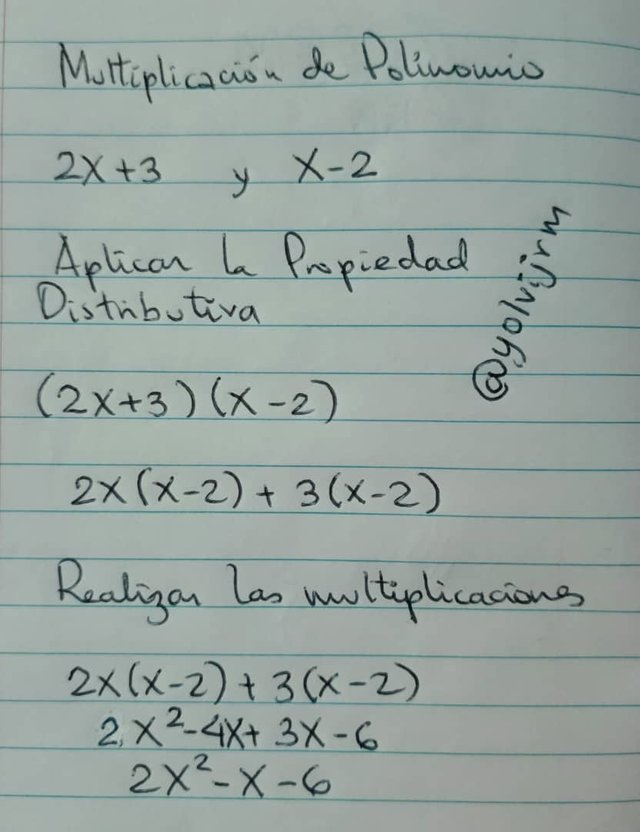
Escenario número 1
Supongamos que hay una persona llamada Ali que tiene una tienda de manualidades y vende cuentas en paquetes x que tienen un costo fijo de $5 más $2 por cada paquete. Ahora tienes que escribir una expresión polinomial para representar el costo total (C) de comprar x paquetes de cuentas considerando que hay un 10% de descuento + También tienes que calcular el costo total de Ali compra 5 paquetes de cuentas.
De acuerdo con la información dada en el planteamiento anterior se tiene que los Cotos Fijos = 5, mientras que el costo por paquete viene dado por 2x, donde x representa el número de paquetes. number. También se nos dice que el Descuento = 10%, es decir 0.1.
En relación a ello se tiene la siguiente expresión, basada en costo total antes del descuento :
Costo antes del decuento = 5 + 2x; siendo x el número de paquetes.
Al aplicar el descuento al costo, la expresión resulta:
Total Costo (C) = 1(5 + 2x) - 0,1 (5 + 2x)
C = 0.9 (5 + 2x)
Una vez que se tiene la expresión del costo total (C) para comprar x paquetes con un descuento del 10%, se procede a calcular el costo total para 5 paquetes :
C = 0.9 (5 + 2x)
C = 0.9(5 + 2(5))
C = 0.5(5 + 10)
C = 0.9(15)
C = 13.5
En relación a ello, se puede decur que el costo total de comprar 5 paquetes con un precio fijo de $5 y un costo de $2 por paquete es $13.50. Es decir que Ali tiene que gastar $13,50 para comprar 5 paquetes de cuentas.
Escenario número 2
Supongamos que hay un agricultor que cosecha x toneladas de trigo y 3x toneladas de cebada. Ahora necesita escribir una expresión racional para representar la relación entre el trigo y la cosecha total en la que hay trigo y cebada y debe simplificar la expresión también al final +. También necesita calcular la relación entre el trigo y la cosecha total si el agricultor está cosechando 4 toneladas de trigo.
De acuerdo con lo planteado en este escenario se tiene que la cantidad de trigo cosechado = x, mientras que la cantidad de cebada = 3x. En relación a ello se plantea la a expresión para la cantidad total cosechada:
Cosecha total = x + 3x
Cosecha total = 4x
Entonces, la relación entre el trigo y la cosecha total se puede escribir así:
Relación = x/4x
Lo cual se podría simplificar a 1/4, para x diferente de 0
Teniendo en cuenta que el agricultor está cosechando 4 toneladas de trigo, la proporción seguirá siendo 1/4, pero verifiquemos también la expresión de la proporción:
Relación = 4/(4*4)
Relación = 4/16
Relación = 1/4
Entonces, se concluye que la relación entre el trigo y la cosecha total siempre será 1/4 siempre que x sea diferente de 0 .

Gustoso de presentar mi participación en este concurso; aprovecho la oportunidad de invitar a @adeljose, @fjjrg y @naka05 a que participen en esta actividad:
Steemit learning challenge S22W5//Polynomial and rational expressions
Las imágenes son de mi propiedad, tomadas con Infinix Note 40 Pro.
Cc: @khursheedanwar
¡Saludos y bendiciones!
