Sort squares of given sorted array of integers

Given a sorted array of integer array containing both positive and negative numbers. We aim to sort the squares of those numbers in place.

Examples

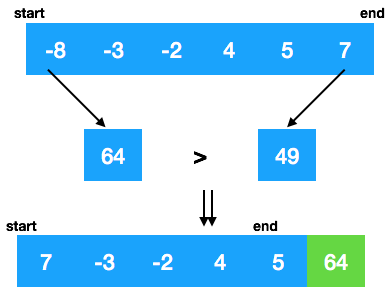
input1 = {-8, -3, -2, 4, 5, 7}
output = {4, 9, 16, 25, 49, 64}

input2 = {-2, -1, 0, 1, 2}
output= {0, 1, 1, 4, 4}

Approach

1. Input is in sorted order and it contains both positive and negative numbers. If we square a negative number which results in a positive number again.
2. As per our input, a large number may be a square of a positive number or a square of a negative number.
3. At the start the largest number may be one of the squares of the first or last numbers of the array. After getting the largest number replace that largest number and put it at the rightmost position.
4. Do the same above steps for the rest of the array until the end reaches to start of the array.

Coding

Recursive Approach

#include <stdio.h>

void solve(int arr[], int start, int end) {
    if(start > end) return;
    // Find largest number.
    int largest = arr[end] * arr[end];
    if(largest < (arr[start]*arr[start])) {
        largest = arr[start]*arr[start];
        //put last element at first.
        arr[start] = arr[end];
    }
    
    // Replace largest at end.
    arr[end] = largest;
    
    // Do the same for the rest of the array.
    solve(arr, start, end-1);
}

// Print array.
void printArray(int arr[], int n) {
    for(int i=0; i<n; i++) {
        printf("%d ", arr[i]);
    }
    printf("\n");
}

int main()
{
    int arr[] = {-8, -3, -2, 4, 5, 7};
    int size = sizeof(arr)/sizeof(arr[0]);
    
    printArray(arr, size);

    solve(arr, 0, size-1);
    
    printArray(arr, size);
    return 0;
}

Iterative approach

void solveIterative(int arr[], int start, int end) {
    int largest;
    while(start <= end) {
        largest = arr[end] * arr[end];
        if(largest < (arr[start]*arr[start])) {
            largest = arr[start]*arr[start];
            //put last element at first.
            arr[start] = arr[end];
        }
        
        // Replace largest at end.
        arr[end] = largest;
        end--;
    }
}

Testing

1. With a casual input as shown in the program.
   arr[] = {-8, -3, -2, 4, 5, 7}
2. With some duplicate values.
   arr[] = {-2, -1, 0, 1, 2}
3. With all same numbers.
   arr[] = {-1, -1, 1, 1}
4. With single number
   arr[] = {-5}

Complexity analysis

Runtime

The above program runs one time for each element which leads to an O(n) runtime complexity.

Space

As we are using recursion, here it uses O(n) space complexity. Whereas the iterative approach uses constant space by avoiding recursions stack.

Conclusion

To conclude we have a linear time complexity solution to sort the squares of an array of sorted integers. Please let us know your views about the problem in the comments.

For more such problems head over to Algorithms

Keep learning!!!