To determine the value of x, we can use the fact that the three terms form an arithmetic sequence, which means that the difference between any two consecutive terms is the same.
We can set up an equation using this information:
(2x + 1) - (x + 6) = (4x - 13) - (2x + 1)
Simplifying this equation, we get:
x - 5 = 2x - 14
Solving for x, we get:
x = 9
Now that we know the value of x, we can use the formula for the nth term of an arithmetic sequence to find the 9th term.
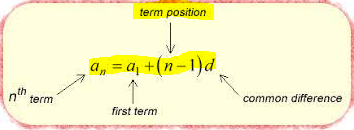
The formula for the nth term of an arithmetic sequence is:
an = a1 + (n - 1)d
where an is the nth term, a1 is the first term, n is the number of the term we want to find, and d is the common difference between consecutive terms.
In this case, we know that:
a1 = x + 6
d = (2x + 1) - (x + 6) = x - 5
Substituting x = 9, we get:
a1 = 15
d = 4
Using the formula, we can find the 9th term:
a9 = a1 + (9 - 1)d
= 15 + 8(4)
= 47
Therefore, the value of x is 9 and the 9th term of the sequence is 47.