When Bitcoin blast-off? When crypto Moon you ask?
So I saw this article with some graphs that are trying to make the chart harder to understand and had some ideas:
https://www.theinvestorspodcast.com/bitcoin-mayer-multiple/
Alright.
Included at the bottom, there's a pretty interesting image someone posted ages ago that happens to demonstrate we're still on a 2014 target. It's just on a log curve. The Investor Podcast references their metric and finds this still to be relevant now.
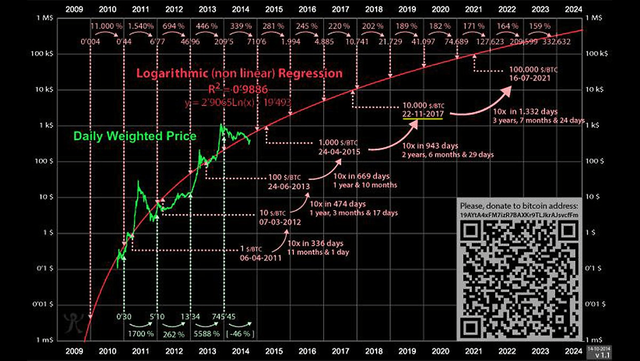
So I wanted to get a more current look, make my own graph and of course some others had thrown a curve on the chart but hadn't done a whole lot of other TA on it or had any indicators running. So here's an updated look at how this has done, ESTIMATED. I Did not recreate this exact 2014 image because fuck that. But if you're looking for a BALLPARK bullish target that isn't based on complete bullshit, here you go on the monthly chart with a vast majority of Bitcoin's history on the chart.
NOTE: Bitcoin never falls beneath the "Baseline" just touches and bounces inside of a channel:
https://www.tradingview.com/x/mMa4Vis9/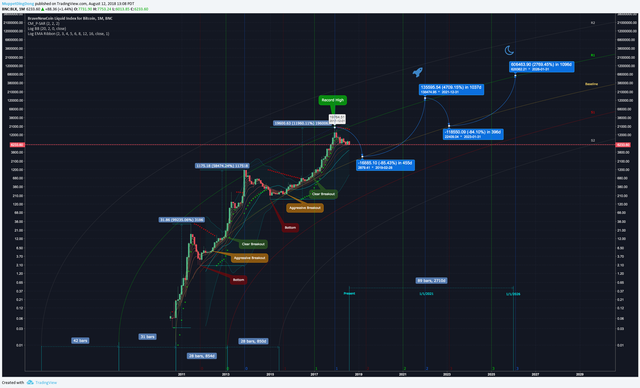
The market cycles are estimated but give reasonably decent estimates for the next major bull runs, particularly emphasizing the end of year boom then massive crash early in the new year, if we remain in massive boom and bust cycles. Over time, the booms and busts will generally get a little longer and little less severe. This doesn't take into account any catalysts or governments regulating banning crypto say like China. Man those mad gains look nice, wouldn't that be great lol?
https://www.tradingview.com/x/z94HIFYm/
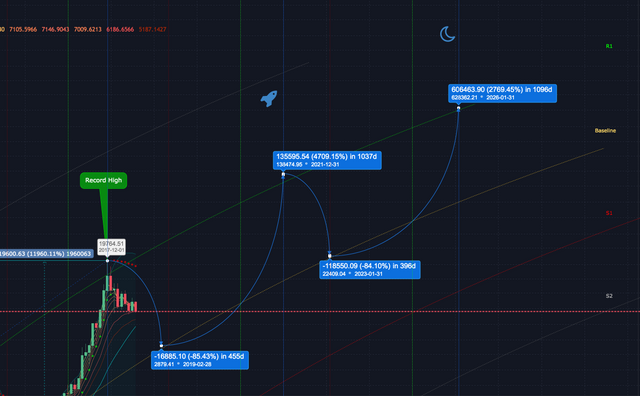
Short Term this isn't what you want to hear. The lows could clear a lot of people out, that target is around $3000 and the bottom is somewhere end of this year early next year :/
When Take-off? Probably mid to late 2021. When Moon? More like mid to late 2025.
BUT great BTFD opportunity and is the move I've been waiting for and will likely be waiting for into the rest of this year. Probably going down and sideways until momentum can build, not merely speculators but users on the network.
USERS ON THE NETWORK is key; developers, miners, investors, speculators, users, banks, wall street, main street everyone. We are still likely not at the bottom. True capitulation looks like it has not remotely happened yet when getting brutally realistic.
Briefly, why I think this is relevant:
"Metcalfe's law states the effect of a telecommunications network is proportional to the square of the number of connected users of the system (n2). First formulated in this form by George Gilder in 1993,[1] and attributed to Robert Metcalfe in regard to Ethernet, Metcalfe's law was originally presented, c. 1980, not in terms of users, but rather of "compatible communicating devices" (for example, fax machines, telephones, etc.).[2] Only later with the globalization of the Internet did this law carry over to users and networks as its original intent was to describe Ethernet purchases and connections.[3] The law is also very much related to economics and business management, especially with competitive companies looking to merge with one another."
https://en.wikipedia.org/wiki/Metcalfe%27s_law
So Tom Lee, Fundstrat Global (and of CNBC fame) has noted this still generally applies today. He is wrong about a lot of shit, because he's a man with an agenda like anyone, but he says it explains 94% of Bitcoins movement and it seems to still be generally accurate:
"'If you double the number of users, you're more than doubling the utility value,' Lee said."
Lee: Yeah, so Metcalfe's a professor. He actually came up with a theorem based on George Gilder, which is the value of a network is the square of the number of users. And so if you build a very simple model valuing bitcoin as the square function number of users times the average transaction value. 94% of the bitcoin moved over the past four years is explained by that equation.
Silverstein: Wow. Just to use an example, so this explains the network effect. Like one fax machine is worthless because there's nobody you can fax. But once all of your friends have fax machines, it becomes very valuable. So has this been effective in valuing things, in the past, that have a strong network but weren't producing any money?
Lee: Yeah, so three use cases — or businesses — where Metcalfe's Law really explain the growth of the market value, is Facebook, Alibaba, and Google. And these are all examples where the number of users — like if you double the number of users, you're more than doubling the utility value. It's a little bit like the commercial in the 70s, you know, Prell. When you tell your friends, and they tell their friends, and so on.
https://www.businessinsider.com/bitcoin-price-how-to-value-fundstrat-tom-lee-2017-10
It just so happens this is relevant to Alphabet Inc, ie. Google (GOOGL)
https://www.tradingview.com/x/RC0Lv8L1/
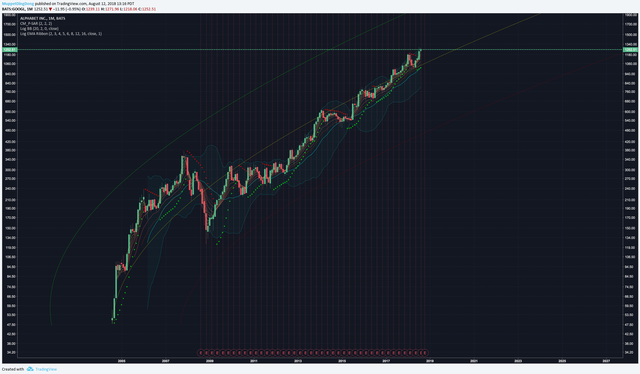.png)
And Facebook (FB), although fuck them right now:
https://www.tradingview.com/x/bA9uVSv9/
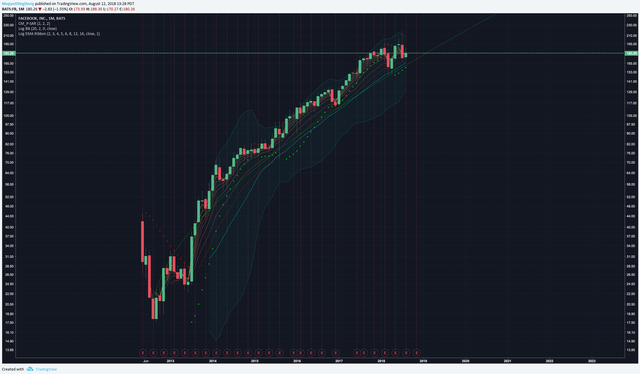.png)
It does suggest that as long as user growth generally keeps going up for Bitcoin, or any derivative crypto and even a lot of current stocks, there is huge upside potential and don't expect it to follow a linear trajectory. A major black swan event or mass government regulation aside (particularly any move made by Dear Leader Dipshit Donnie), I think you can expect long term this graph will remain relevant. This does assume crypto finds its niche and sticks around which it seems highly possible.
Just a random guy giving his opinions on the internet, as it tradition. blablabla disclaimer.
Interesting analysis, thanks for sharing.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
TY Appreciate the appreciation.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Hi! I am a robot. I just upvoted you! I found similar content that readers might be interested in:
https://en.wikipedia.org/wiki/Metcalfe%27s_law
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit