Pythagoras Theorem is one of the best known formulae in mathematics, and one simple proof is demonstrated, along with some background about Pythagoras himself.
Pythagoras Theorem states that
In a right-angled triangle, the square on the hypotenuse is equal to the sum of the squares on the other two sides.
This simple statement is learned by most students at an early stage, typically in eighth grade, and is taken as true. The theorem is extremely useful in everyday life, and is used in innumerable applications. It can be easily proven using simple geometry and algebra.
Pythagoras of Samos
Pythagoras lived from around 582 to 507 B.C. He was born in Samos, Greece, although he moved to Crotona, where he founded the Pythagorean Cult. This was a secret society, and most of its rituals and beliefs are lost through the passage of time, as well as the fact that was a secret society. However, it is known that their basic tenet was that everything from music to justice could be expressed using numbers.
Pythagoras Proof Definitions
Right-angle: An angle of ninety degrees, formed by the perpendicular intersection of two straight lines.
Hypotenuse: In a right-angled triangle, the side opposite the right-angle.
Area of a square: The length times the breadth. Since length = breadth in a square, the area equals the length (or breadth) squared.
Area of a triangle: The length times the breadth divided by two. (This is easily proven by drawing a diagonal inside a rectangle.)
The notation A^2 means the number "A" squared
The notation 2.X.Y means 2 times X times Y
Proof of Pythagoras Theorem
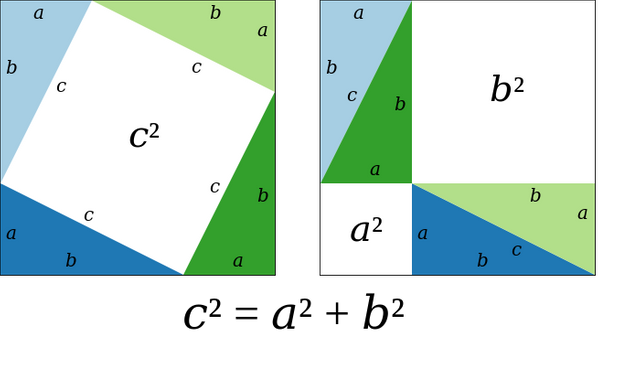
Figure 1 shows a large square with a smaller square inside it. Each side of the larger square has a length of X + Y units. The smaller square, which just touches the sides of the outer square, has sides of length Z. Each of the four triangles are right-angled, with a hypotenuse of length Z.
The area of the large square must equal the area of the small square plus the area of the four coloured triangles, so
(X + Y)^2 = Z^2 + 4.X.Y.(1/2)
Now (X + Y)^2 = (X^2 +2.X.Y + Y^2), so
X^2 + 2.X.Y + Y^2 = Z^2 + 2.X.Y
Cancelling out the 2.X.Y term on each side gives the final result:
X^2 + Y^2 = Z^2
Q.E.D.
Summary of Pythagoras Theorem
Pythagoras theorem is one of the best known and most useful formulae in use today. It is learned by most pupils before their teenage years. There are many proofs of it, in fact the mathematical prodigy Paul Erdos could prove the theorem in ten different ways by the age of fourteen. The proof shown is remarkably simple, and uses only first level geometry and basic algebra to complete the proof.
The field of proofs in mathematics in general, and some well-known proofs in particular, can be downloaded from Math Proofs Demystified.
Source:
Math Proofs Demystified 1st Edition, Kindle Edition by Stan Gibilisco