The Magic Squares of Benjamin Franklin

 

Magic Squares have a long and mystifying history. A perfect magic square is defined as a square grid filled with an arrangement of numbers where the rows, columns, and diagonals of the square add to the same magical sum. The first known magic square was the Lo Shu magic square and dates back to ancient China. Intriguing many people through the ages, the magic square would eventually provide amusement for Benjamin Franklin.

16x16 Magic Square

Benjamin Franklin is known to have experimented with the fanciful numerical tables for much of his life. In the book entitled Magic Squares and Cubes (Open Court Publishing 1908), a copy of a letter from Franklin to his friend Peter Collinson in London expressed his long time interest and attraction to the squares. He remarked in the letter that during his youth he created many magic squares with the skilful speed equal to the time it simply took to write the series of numbers needed.

Franklin also described in the letter mentioned above a 16X16 example of his as “the most magically magical of any magic square ever made by any magician.” At the time it certainly was considered one of the most excellent and even today people still would agree. Although not exactly a perfect magic square because the straight diagonals differ in sums, the square does display the qualities of rows and columns adding to equal ‘magic sums’ and features other amazing unique characteristics.

source

The sum for Franklin’s 16X16 gridded square is 2056. This number is found within any 4X4 square pulled from the 16X16, the corner numbers with the center four numbers, multiple bent diagonal rows, and many additional methods displaying various symmetrical designs. The square holds curiosities which are admired and studied yet today.

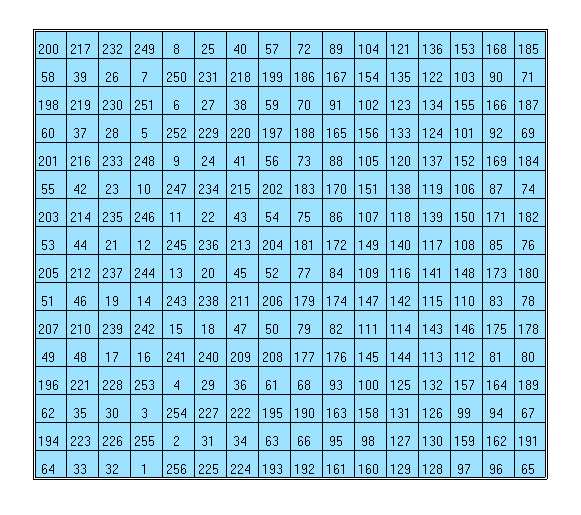
Method for Building a Magic Square

Since Franklin constructed many magic squares of various sizes and properties understanding how he built some of his smaller squares reveals a method he applied for filling grids of superior dimensions. His famous 8X8 magic square preceded the larger and contains similar characteristics as his square of 16. The same is true for his square of 4.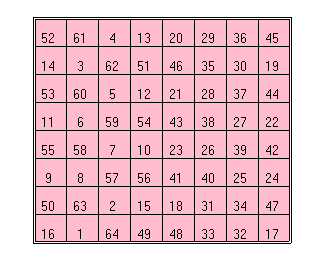

source

It would seem these three magic squares were built by following the same basic system. For example, the numbers of the series for the 4X4 square can be written in two equal columns, like so:

1-16

2-15

3-14

4-13

5-12

6-11

7-10

8—9

Splitting the rows in half will provide the numbers used for the rows of the square by taking the outer numbers starting at center and going around clockwise for the top half (4,1,16,13) and counter clockwise for the bottom (5,8,9,12). Then take the inner numbers going counter clockwise on top (14,15,2,3) and continuing on the opposite side going clockwise for the bottom (11,10,7,6). It may help to imagine drawing a number 8 for the inner numbers.

The outer numbers are then placed in the first and last rows and the inside numbers on the inside like so;

5-8-9-12

14-15-2-3

11-10-7-6

4-1-16-13

This system is applied for making larger, even sized grids by splitting the rows accordingly and working the numbers outward from centers. It is only one of the many methods Franklin used for creating his squares.

Magic Squares and More

Benjamin Franklin not only enjoyed fashioning magic squares, he also produced magic circles. His fascination with numbers went beyond the ordinary. Magic squares are believed by many to hold and convey mystical powers and knowledge. The influence and nature of numbers is an intricate study and one which Franklin seems to have pursued. With his many arrangements and formations, he left a collection of mystifying numbers for all to ponder.

Sources:

• Andrews, W.S., Magic Squares and Cubes, Open Court Publishing, 1908
• Ben Franklin's Amazing Magic Square: http://www.math.wichita.edu/~richardson/franklin.html
• Ben Franklin's 8x8 Magic Square http://www.math.wichita.edu/~richardson/littleben.html
• Pasles, Paul, Benjamin Franklin’s Numbers, Princeton University Press