RE: Learn Python with Steem #10 #11 笔记

You are viewing a single comment's thread from:

Learn Python with Steem #10 #11 笔记

in blog •  6 years ago 

这里是个警告，错误信息可能在其他地方。

blog
6 years ago by

Downvoting a post can decrease pending rewards and make it less visible. Common reasons:

  • Disagreement on rewards
  • Fraud or plagiarism
  • Hate speech or trolling
  • Miscategorized content or spam

Submit
$0.00
    9
    Authors get paid when people like you upvote their post.
    If you enjoyed what you read here, create your account today and start earning FREE STEEM!
    Sort Order:  
  • Trending
    • [-]
      ·  6 years ago 

    我看你貼出來也有相關警告，但是你最後能出結果？

    Posted using Partiko Android

    Downvoting a post can decrease pending rewards and make it less visible. Common reasons:

    • Disagreement on rewards
    • Fraud or plagiarism
    • Hate speech or trolling
    • Miscategorized content or spam

    Submit
    $0.00
      [-]
        ·  6 years ago 

      结果有的，你的图是空白的？

      Downvoting a post can decrease pending rewards and make it less visible. Common reasons:

      • Disagreement on rewards
      • Fraud or plagiarism
      • Hate speech or trolling
      • Miscategorized content or spam

      Submit
      $0.00
        [-]
          ·  6 years ago 

        Downvoting a post can decrease pending rewards and make it less visible. Common reasons:

        • Disagreement on rewards
        • Fraud or plagiarism
        • Hate speech or trolling
        • Miscategorized content or spam

        Submit
        $0.00
          [-]
            ·  6 years ago 

          多謝，明天我還搞不定就拿來看看😆

          Posted using Partiko Android

          Downvoting a post can decrease pending rewards and make it less visible. Common reasons:

          • Disagreement on rewards
          • Fraud or plagiarism
          • Hate speech or trolling
          • Miscategorized content or spam

          Submit
          $0.00
            [-]
              ·  6 years ago 

            还没看，但是根据你之前告诉我的修改，总算改对了，为什么说总算，因为新手的我看代码只能一知半解~
            改完后能正常运行了，也没错误提示，就是不见图，虽然知道plt是能预览，但是我不知道具体要怎么做（感觉ax并没有和plt有关联起来），对于这个的参数也不熟悉，跑去github看别人的，确定少了句

            plt.show()

            哈哈哈，愉快的显示出来了，我表示我要稍微去了解下这两货！

            Downvoting a post can decrease pending rewards and make it less visible. Common reasons:

            • Disagreement on rewards
            • Fraud or plagiarism
            • Hate speech or trolling
            • Miscategorized content or spam

            Submit
            $0.00
              [-]
                ·  6 years ago (edited)

              文件我存了，非常感谢！图虽然画出来了，但是我怎么觉得和数据不对呐？
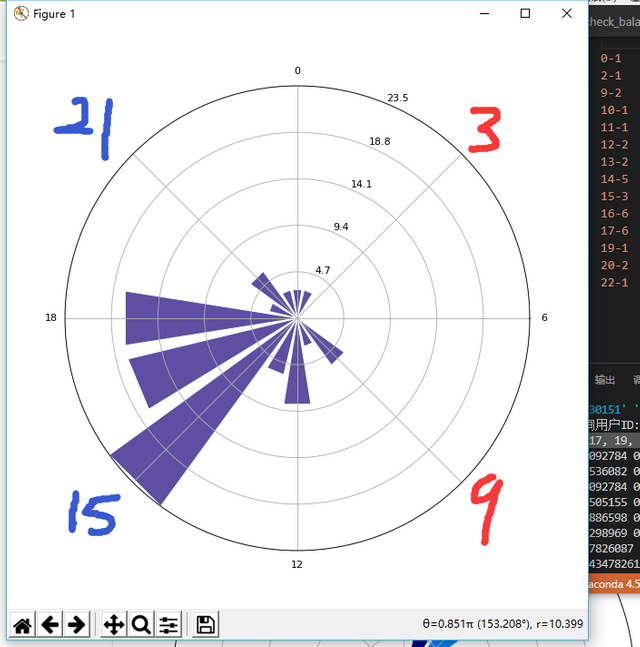
              image.png
              右边文字显示的是“时间”-“次数”
              每一圈的数字（4.7、9.4、14.1、18.8、23.5）好像是半径，但是我没理解怎么算出来的，代表什么？ T T~

              Downvoting a post can decrease pending rewards and make it less visible. Common reasons:

              • Disagreement on rewards
              • Fraud or plagiarism
              • Hate speech or trolling
              • Miscategorized content or spam

              Submit
              $0.00
                [-]
                  ·  6 years ago 

                确实不对！感谢提出来。

                它默认划分为16个扇形，时间和角度没有对应，360/16=22.5°，扇形的位置有重合和偏差。
                需要设置参数sector为：nsector=24

                每一圈的数字（4.7、9.4、14.1、18.8、23.5）是半径（极坐标中的极径）。计算方法是：
                在0到最大极径之间划分6等分，去掉其中的0，取其中5个数作为极径的标签。
                在set_radii_angle(self, **kwargs)这个函数中是这么写的：

                 N = 5
        rmax = self.get_rmax()
        radii = np.linspace(0, rmax, N + 1)
        if rmax % N == 0:
            fmt = "%d"
        else:
            fmt = "%.1f"
        radii_labels = [fmt % r for r in radii]
        # radii_labels[0] = ""  # Removing label 0
        self.set_rgrids(radii=radii[1:], labels=radii_labels[1:],
angle=self.radii_angle, **kwargs)

                可以参照这个函数的计算方法，自己修改其标签为次数。

                我得在文章中做些修正。非常感谢！

                Downvoting a post can decrease pending rewards and make it less visible. Common reasons:

                • Disagreement on rewards
                • Fraud or plagiarism
                • Hate speech or trolling
                • Miscategorized content or spam

                Submit
                $0.00
                  [-]
                    ·  6 years ago (edited)

                  请教个问题“**kwargs”是什么变量或者参数？

                  count, _ = np.histogram(time, bins=24)

                  这句话我有点不理解‘,_’是什么？“count = np.histogram(time, bins=24)”这样的我可以理解，两种有什么区别？

                  Downvoting a post can decrease pending rewards and make it less visible. Common reasons:

                  • Disagreement on rewards
                  • Fraud or plagiarism
                  • Hate speech or trolling
                  • Miscategorized content or spam

                  Submit
                  $0.00
                    [-]
                      ·  6 years ago 

                    "**kwargs"是个字典，接收长度可变的关键字参数。python可变参数的用法可以参考文章

                    np.histogram()这个函数的功能是计算直方图，它的返回值是个元组：

                    return n, bin_edges

                    所以用两个变量来接收这个函数的返回值。count, _ = np.histogram(time, bins=24)的意思相当于：将n赋值给count，bin_edges赋值给_，由于不需要用到bin_edges这个结果，就没给这个变量起有意义的名字，写了个下划线。

                    如果写成count = np.histogram(time, bins=24)的话，count会作为一个元组，包含两个数据：count = (n,bin_edges)

                    image.png

                    image.png

                    说下n,bin_edges的含义，n是一个列表，里面的值是各个直方的高度，也是频次;
                    bin_edges 也是一个列表，里面的数据表示每组数据的组距，每个直方的宽度，范围是左闭右开的，如上图：在[0,0.95833333)的范围内的数有1个，在[0.95833333,1.91666667)的范围内的数有1个......
                    但最后一组数据的范围是闭区间：在[22.04166667,23]的范围内的数有1个。

                    Downvoting a post can decrease pending rewards and make it less visible. Common reasons:

                    • Disagreement on rewards
                    • Fraud or plagiarism
                    • Hate speech or trolling
                    • Miscategorized content or spam

                    Submit
                    $0.00