SISTEM NUMERASI MESIR KUNO

Dalam perkembangan matematika ada banyak sistem numerasi, salah satunya adalah sistem numerasi Mesir. Topik ini di bahasa dalam perkuliahan matematika, diantaranya dalam mata kuliah teori bilangan. Tetapi pembahasan dalam mata kuliah tidaklah selengkap yang diharapkan. Misalnya tentang simbol-simbol numerasi Mesir, bahwa ada beberapa simbol seperti pada sistem bilangan hieratic yang tidak tercantum dibuku.

Sistem Bilangan Zaman Mesir Kuno
Bangsa Mesir Kuno telah mengenal alat tulis sederhana menyerupai kertas yang disebut papyrus. Mereka membuat tulisan berbentuk gambar-gambar dengan menggunakan sejenis pena sengan tinta berwarna hitam atau merah. Tulisan Mesir Kuno sering disebut tulisan Hieroglif, dan tulisan ini ditemukan dalam bentuk gambar pada papyrus ataupun guratan pada batu atau potongan kayu. Tulisan Mesir Kuno diperkirakan berkembang pada tahun 3400 S.M. Tulisan pada zaman mesir ini ditulis dari kata papu yaitu semacam tanaman. Sistem Numerasi Mesir Mesir Kuno bersifat aditif, dimana nilai suatu bilangan merupakan hasil penjumlahan nilai-nilai lambang-lambangnya.
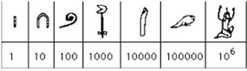
Notasi matematika Mesir Kuno bersifat desimal (berbasis 10) dan didasarkan pada simbol-simbol hieroglif untuk tiap nilai perpangkatan 10 (1, 10, 100, 1000, 10000, 100000, 1000000) sampai dengan sejuta. Tiap-tiap simbol ini dapat ditulis sebanyak apapun sesuai dengan bilangan yang diinginkan, sehingga untuk menuliskan bilangan delapan puluh atau delapan ratus, simbol 10 atau 100 ditulis sebanyak delapan kali. Dengan ini berarti bahwa mereka memiliki simbol terpisah untuk satuan, puluhan, ratusan, ribuan, puluh ribuan, ratus ribuan, dan jutaan.
A.Angka Hieroglif

Untuk satuan adalah sebuah garis lurus, lengkungan ke atas untuk puluhan, lengkungan setengah lingkaran menyamping (seperti obat nyamuk) untuk ratusan, dan untuk jutaan dilambangkan dengan simbol seorang laki-laki yang menaikkan tangan. Penulisan hieroglif dapat dimulai dari kanan ke kiri, kiri ke kanan, atau dari atas ke bawah dan dari bawah ke atas, tetapi biasanya dimulai dari kanan ke kiri (seperti dalam penulisan Arab, walaupun dalam penulisan formal zaman sekarang ini menggunakan kiri ke kanan).

Misalnya untuk membuat bilangan 276, ada lima belas simbol yang diperlukan: dua simbol “ratusan”, tujuh simbol “puluhan”, dan enam simbol “satuan”. Contoh tulisan bilangan 276 dalam hieroglif terlihat pada batu ukiran dari Karnak, berasal dari sekitar 1500 SM, dan sekarang berada dipamerkan di Louvre, Paris.

Penulisan angka desimal:
Dalam menuliskan bilangan, susunan desimal terbesar ditulis lebih dahulu. Bilangan ditulis dari kanan ke kiri. Berikut contoh penulisan angka 46,206
Untuk penulisan tanda koma, lihat simbol hiroglif yang tandanya berbalik arah. Misalnya pada penulisan angka 46,206 simbol yang berbalik arah adalah 40000 dan 6000. Sedangkan penulisan simbol 200 dan 6 tidak berbalik arah. Penulisan tanda koma ditulis setelah angka yang berbalik arah yakni pada angka 46.000.
Cara Penulisan Pecahan
Pecahan untuk orang Mesir kuno terbatas pada pecahan tunggal (dengan pengecualian dari yang sering kali digunakan 2/3 dan kurang sering digunakan 3/4). Sebuah pecahan tunggal adalah bentuk 1/n dimana n adalah bilangan bulat dan ini diwakili dalam angka hieroglif dengan menempatkan simbol yang mewakili sebuah “mulut”, yang berarti “bagian”, di atas nomor tersebut.
Berikut adalah beberapa contoh:

  Perhatikan bahwa ketika bilangan yang mengandung terlalu banyak simbol “bagian”, ditempatkan di atas bilangan bulat, seperti dalam 1/249 , maka simbol “bagian” ditempatkan di atas “bagian pertama” bilangan. Symbol diletakkan di atas bagian pertama karena bilangan ini dibaca dari kanan ke kiri.

Penjumlahan sistem bilangan Mesir
Penjumlahan sistem bilangan mesir hampir serupa dengan penjumlahan dengan masa kini yang berbeda hanyalah simbolnya.
456 + 265 = 721 = 721

Perkalian pada sistem bilangan Mesir
Matematika papyrus Rhind adalah salinan dari sebuah rata rata krja sebelumnya, Matematika papyrus rhind disalin dari seseorang penulis yang bernama Ahmose ditahun 1650 SM. Dimana pada waktu itu, Joseph menjadi gurbenur di mesir. Alexander Henry Rhind memperolehnya di luxor, Mesir ditahun 1858 dan kemudian membelinya dimuseum inggris pada tahun 1865.Matematika Rhind papyrus diperkenalkan dengan menjanjikan pembaca melalui kalimat berikut, “ Dengan mempelajari semua hal yang baik, semua wawasan akan tetap ada dan pengetahuan dari rahasia yang tersembunyi, akan terungkap. Pada faktanya, hal ini merupakan deretan pemecahan masalah matematika dasar, sebuah garis besar houm untuk penulis yang bercita cita tinggi, Penulis tersebut harus dapat menghitung dengan pasti berapa banyak batu bata yang dibutuhkan untuk membangun jalan dengan kemiringan tertentu dan berapa banyak papan roti yang dibutuhkan untuk memberi makan budak pekerja dan sebagainya.
Jauh sebelum kalkulator atau bahkan matematika modern, orang Mesir telah menemukan cara jitu menentukan jumlah bilangan besar dengan cepat. Berikut cara perkalian numerasi Mesir:

Ø Perkalian Dengan Cara Doubling
Perkalian dalam sistem doubling dikerjakan dari pengulangan pelipat gandaan bilangan dengan unsur pengalinya kemudian menjumlahkannya. Contohnya 13 x 12 = ? Buatlah garis untuk memisahkan dua kolom. Isi kolom ke bawah di sebelah kiri, dimulai dengan nomor 1. Gandakan dan tulis 2 dibawahnya, lalu gandakan 2 itu sehingga mendapatkan angka 4, terus digandakan sampai angkanya tidak melebihi yang dikalikan. Isilah kolom kanan, tuliskan nomor yang ingin anda kalikan (dalam hal ini, adalah 12). Dibawah 12, gandakan dan tulis 24. Gandakan lagi 24 dan tulis 48, Terus sampai sebanyak kolom kiri (lihat gambar).

Sekarang cari angka di kolom kiri yang kalau ditambahkan akan menghasilkan angka pertama yang ingin dikalikan (dalam soal ini, 13). Angka 1 + 4 + 8= 13, lalu garis bawahi nomor dikolom kanan diseberang nomor tersebut. Maka yang digaris bawahi di kolom kanan adalah (12 + 48 + 96) dan kamu jumlahkan akan mendapatkan 156, yang adalah jawaban tepat dari 13 x 12 = 156
Ø Perkalian dengan Cara Halving
Perkalian dalam sistem halving berbeda dengan doubling untuk mempermudah langsung saja pada contoh. Contohnya 13 x 12 = ? Buatlah garis untuk memisahkan dua kolom. Isi kolom di sebelah kiri, dimulai dengan membagi angka yang dikali (dalam hal ini 13) dibagi dengan 2 maka hasilnya 6 (untuk 0,5 tidak di tulis). Isilah kolom kanan, tulislah nomor yang ingin anda kalikan (dalam hal ini adalah 12). Dibawah 12, gandakan dan tulis 24. Gandakan lagi 24 dan tulis 48. Terus sampai sebanyak kolom kiri (lihat gambar)

 13            12
 6              24
 3              48
 1              96

Sekarang cari angka di kolom kiri yang ganjil, yaitu angka 13, 3, dan 1. Lalu garis bawahi nomor di kolom kanan diseberang nomor tersebut. Maka yang digaris bawahi di kolom kanan adalah (12 + 48 + 96) dan kamu jumlahkan akan mendapatkan 156, yang adalah jawaban tepat dari 13 x 12 = 156.

Pembagian pada sistem bilangan Mesir
Pembagian dalam sistem bilangna mesir dikerjakan dari pengulangan pelipat gandaan bilangan dengan unsur pembaginya kemudian menjumlahkannya. Contohnya 98 : 7 = ? Buatlah garis untuk memisahkan dua kolom. Isi kolom ke bawah di sebelah kiri, dimulai dengan nomor 1. Gandakan dan tulis 2 dibawahnya, lalu gandakan 2 itu sehingga mendapatkan angka 4, terus digandakan sampai angkanya tidak melebihi yang dibagi. Isilah kolom kanan, tulislah nomor pembaginya (dalam hal ini, adalah 7). Di bawah 7, gandakan dan tulis 14. Gandakan lagi 28 dan tulis 56, dan seterusnya. (lihat gambar).

 1                7
 2              14
 4              28
 8              56

    Sekarang cari angka dikolom kanan yang kalau ditambahkan akan menghasilkan angka yang dibagi (dalam soal ini, adalah 98). Maka angkanya 14 + 28 + 56 = 98, lalu garis bawahi nomor di kolom kiri diseberang nomor ini. Maka yang di garis bawahi di kolom kiri adalah (2 + 4 + 8) dan kamu dapat mendapatkan 14, yang adalah jawaban tepat dari 98 : 7 = 14

B. Sistem Bilangan Hieratic
Selama Kerajaan Baru masalah matematis disebutkan pada Papyrus Anastasi 1, dan Wilbour Papyrus dari waktu Ramesses III mencatat pengukuran lahan. Angka hieroglif agak berbeda dalam periode yang berbeda, namun secara umum mempunyai style serupa. Sistem bilangan lain yang digunakan orang Mesir setelah penemuan tulisan di papirus, terdiri dari angka hieratic.
Angka ini memungkinkan bilangan ditulis dalam bentuk yang jauh lebih rapi dari sebelumnya saat menggunakan sistem yang membutuhkan lebih banyak simbol yang harus dihafal. Ada simbol terpisah untuk:

1, 2, 3, 4, 5, 6, 7, 8, 9,
10, 20, 30, 40, 50, 60, 70, 80, 90,
100, 200, 300, 400, 500, 600, 700, 800, 900,
1000, 2000, 3000, 4000, 5000, 6000, 7000, 8000, 9000

Berikut adalah versi dari angka hieratic

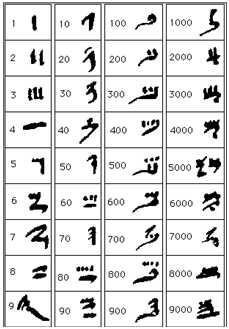
Sistem bilangan ini dapat dibentuk dari beberapa simbol. Angka 9999 hanya memiliki 4 simbol hieratic sebagai pengganti 36 hieroglif. Salah satu perbedaan utama antara angka keramat dan system bilangan kita adalah angka keramat tidak membentuk system posisi sehingga angka tertentu dapat ditulis dalam urutan apapun.
Berikut ini adalah salah satu cara orang Mesir menulis 2765 dalam angka hieratic.

Berikut ini adalah cara kedua menulis 2765 dalam angka hieratic dengan urutan terbalik.

Perhitungan Waktu Bangsa Mesir Kuno
Pada sekitar tahun 1500 SM, orang-orang Mesir Kuno menggunakan sistem bilangan berbasis 12, dan mereka mengembangkan sebuah sistem jam matahari berbentuk seperti huruf T yang diletakkan di atas tanah dan membagi waktu antara matahari terbit dan tenggelam ke dalam 12 bagian.

Para ahli sejarah berpendapat, orang-orang Mesir Kuno menggunakan sistem bilangan berbasis 12 didasarkan akan jumlah siklus bulan dalam setahun atau bisa juga didasarkan akan banyaknya jumlah sendi jari manusia (3 di tiap jari, tidak termasuk jempol) yang memungkinkan mereka berhitung hingga 12 menggunakan jempol.
Jam matahari generasi berikutnya sudah sedikit banyak merepresentasikan apa yang sekarangkita sebut dengan “jam”. Sedangkan pembagian malam menjadi 12 bagian, didasarkan atas pengamatan para ahli astronomi Mesir kuno akan adanya 12 bintang di langit pada saat malam hari. Dengan membagi satu hari dan satu malam menjadi masing-masing 12 jam, maka dengan tidak langsung konsep 24 jam diperkenalkan. Namun demikian panjang hari dan panjang malam tidaklah sama, tergantung musimnya (contoh: saat musim panas hari lebih panjang dibandingkan malam).
Ternyata bangsa Mesir Kuno telah menggunakan hieroglif sebagai alat hitung sejak ribuan tahun sebelum masehi. Sistem perhitungan mereka pada saat itu telah menggunakan basis 10. Bangsa mesir Kuno juga telah mengembangkan operasi aritmetika (penjumlahan, pengurangan, perkalian, dan pembagian). Selain simbol hieroglif bangsa mesir juga menggunakan simbol hieratic. Hal terebut menandakan bahwa betapa hebatnya manusia bahkan sejak zaman dahulu. Meski tekhnologi tak secanggih saat ini mereka telah mengenal banyak hal yang pada akhirnya berguna bagi kita dan dapat kita manfaatkan sampai saat ini. Semoga tulisan ini bermanfaat bagi pembaca khususya pembaca di bidang Matematika, agar mengetahui sejarah bilangan khususnya sejarah dari sistem nunerasi Mesir Kuno.

Sumber :
http://myevi21.blogspot.co.id/2015/07/sistem-numerasi-mesir-kuno_66.html?m=1

Daftar Pustaka:

Anonim. (2013). Perkembangan Matematika Mesir Kuno. [Online]. http://isookamanah.blogspot.com/2013/02/fsm-group-task-perkembangan-matematika_514.html. [30 Maret 2015]

Amir, Ali. 2010. Cara Jitu Menghitung Orang Mesir Kuno.http://erabaru.net/iptek/55-iptek/13349-cara-jitu-menghitung-orang-mesir-kuno. [30 Maret 2015]

Rha. 2012. Sejarah Perhitungan Waktu. http://www. infospesial. net/news/sejarah-perhitungan-waktu/. [ 30 Maret 2015]