📌Task 1

Explain difference between linear and non linear systems of equations. Provide examples of each type of system of equation and describe their general forms.

🔵Linear system of equation.

A system of equations which includes two or more linear equations is refered as linear system of equations.

A linear equation have maximum power of one for variables. This is also known as one degree equation.

General form of linear system of equation.

am + bn - c = z
Here in this eq a , b , c and z are constants while n and m are variable. Both variable are raise to power of 1.

Algebraic example

a - 4b = -8
2a + 3b = 11

Solution:
we can solve this example as follow
2( a - 4b) = 2(-8)
2a - 8b = - 16
( 2a + 3b = 11)-(2a - 4b = -16)
7b = 27
b= 27/11
b = 2.45
To find the value of b we can put the value of y in any of equations
a - 4b = -8
a- 4 ( 2.45) = - 8
a - 9.8 = -8
a = -8+9.8
a = 1.8

Practical life example

Consider a Vander sold two type of corn 🌽 one boiled and other roasted . The boiled sold for 50 PKR and roasted for 60 PKR.
If he sold 75 boiled and a total sail is about 7050 PKR then how much of roasted corn are sold out
We can write algebraic expressions as follow
50x + 60y = 7050 (i)
and x= 75
Put the value of in equation (i)
50(75) + 60 y = 7050
on multipling we get
3750 + 60y= 7050
Rearrange the above equation
60y = 7050 - 3750
60y = 3300
devide both sides by 60 we get
y= 55

🔵Nonlinear system of equations

A nonlinear system of equations consist on more than one equations,in which at least one equation is a non linear equation.

A non linear equation can be defined as an algebraic statement in which the highest power of variable is more then one.

General form of nonlinear system of equation

m^3 - an^3 + bo = z
m + n = x
m+ o = y

Here in above equation a , b and z are constants, while m ,n and o are variables. As we can see m and n both have a power more than 1( cubic terms). This is a simple nonlinear system of equations.

Algebraic example

2a^2 + 3b= 12
a + b= 4
Solution:
For solving this nonlinear system of equation we can start to find the value of b in terms of a as follow
b = 4-a
By putting the value of b we get
2 a^2 + 3 (4-a) =12
For simplification I multiple 3 with 4-a an get
2a^2 + 12 - 3a = 12
Combine like terms
2a^2 - 3a = 12 - 12
2a^2 - 3a = 0
By taking a into common we get
a(2 a - 3)= 0
Here we get two possible values of a
a = 0
And 2a- 3= 0 or a = 3/2
For both values of a we can calculate values for b
For a= 0 , b is equal to 4
For a = 3/2 , b is equal to 5/2

Practical life example

Consider an acre of oranges is sold at 300K PKR . If this acre have two different type of oranges i.e kinnow and Blood oranges. And a and b are prices for kino and blood oranges (per ton) respectively and the revenue for kino is quadratically increases with respect to it's price , while the margin of profit in case of blood oranges is thrice for it's price so we can write revenue and production equation as follow

x^2 + 3y = 300000 (PKR)
XY = 13000 ( tons)

Some important points in differences

Linear system of equations

🔹Variables must raised to power one
🔹 Straightline equations in ghrapical representation
🔹Have a unique or infinite solutions
🔹solved via algebraic or ghraphical method

Nonlinear system of equations
🔹Among all at least one variable must have power more than one
🔹 Form curve ,if represent in graphical form
🔹Have many complex solutions
🔹Solved via numerical methods

📌Task 2

Describe any one method for solving system of linear equations and share atleast one step by step algebric example.

The method I'm going to explain is matrix inversion method for solving a system of linear equations.
Let's start

a+b= 70 ....(i)
9a- 3b=18 ....(ii)
The equation(ii) require some simplification so devide it with 3 and we get.
3a-b=6 ....(iii)

✒️Now by using eq (i) and (iii) we can write it's matrix form

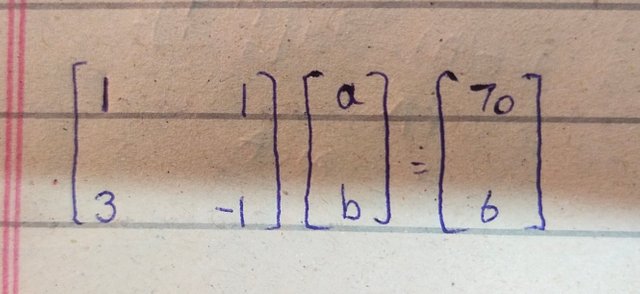
Here [1 1 ,3 -1 ] = A , [a b] = X and [70 6 ]= B.
Matrix equation for above scenario is

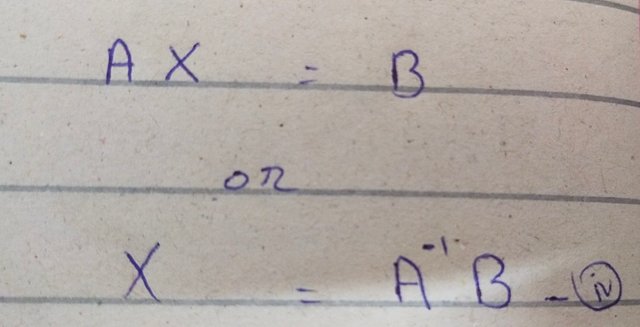
As we know that inverse of A is given as

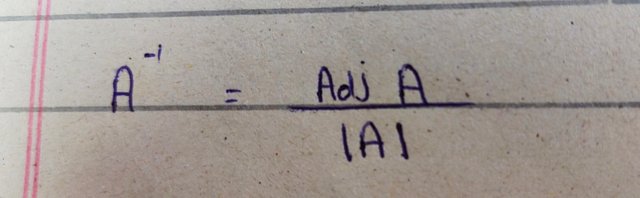
Here the adjoint of A obtained by exchanging the entries of first diagonal and changing the sign of second diagonal in saqure matrix

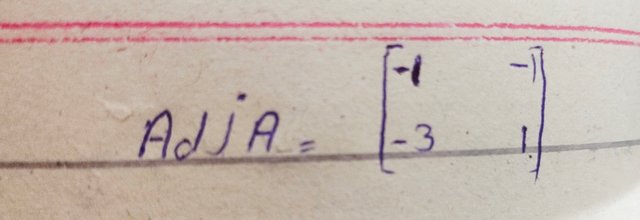
Now we have to find the determinants of A
Besoz
|A|=detA

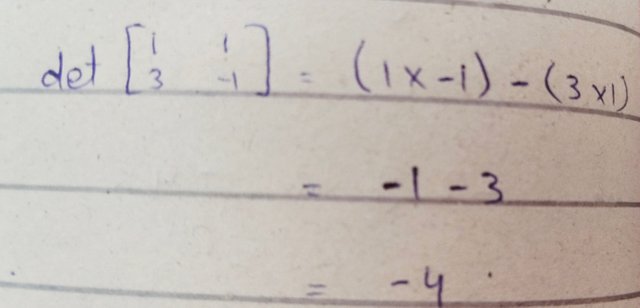
By putting the values of adjA and |A| in equation to find the inverse of A as follow

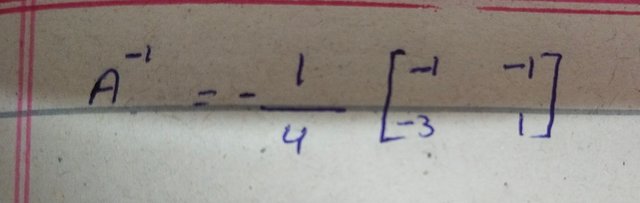
After this we can put the values of inverse of A and , B and X in equation 4 as follow

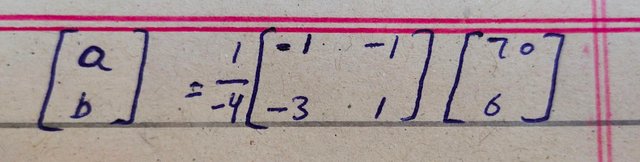
In following image I perform multiplication and then addition and subtraction

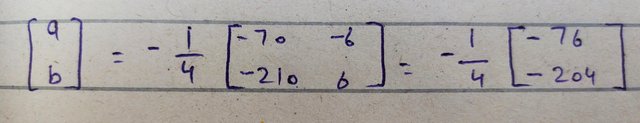
Now I for further simplification I multiply the negative value with the entries within the matrix as follow

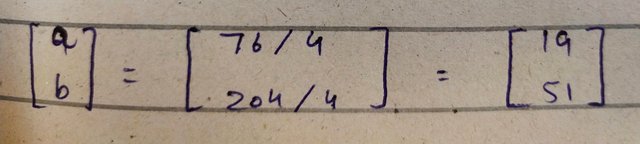
In above picture the final value is also calculatef by dividing the 76 and 204 by 4.
Now the final answer is given as

📌Task3

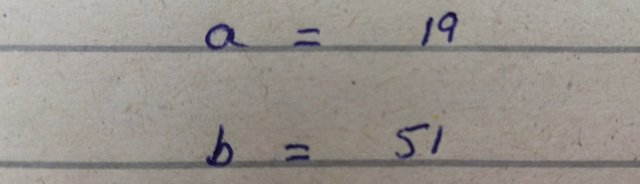
You need for solving following system of linear equations:

The algebraic expression(a) is

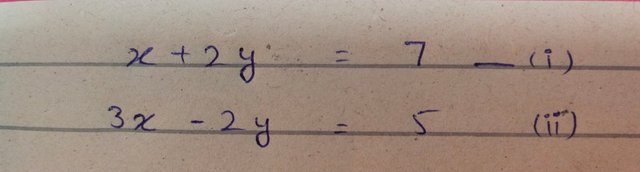
I assigned the two roman numbers to the given expression for the sake of convenience.
To solve these linear expressions I'm going to use the elimination method. In this methodology the step is to perform essential multiplication to get the similar coefficient of variable. But on here in our case we have the same coefficients for "y" variable, so there is no need for this step .

Step1

In our step number 1 we have to add both the equation as given below

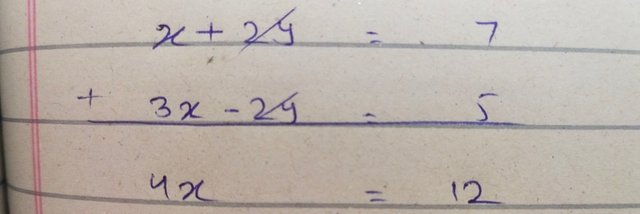
This step gives us an expression wich needs further simplification.

Step2

To simplyfy above expression I devide both sides of equations with with 4 wich gives the value of first variable i.e of x

Step3

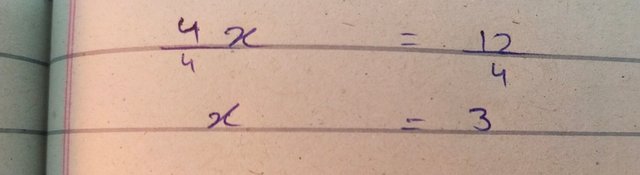
Now to calculate the value of "y" we put the value of "x" into equation (ii)

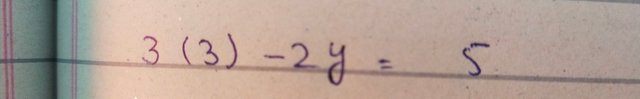
Now for simplification I multiple the the coefficient 3 with the value of x and it gives the following expression

Step4

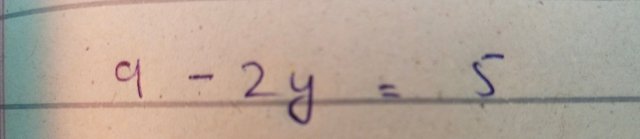
Here rearrange the equation to unify the like terms

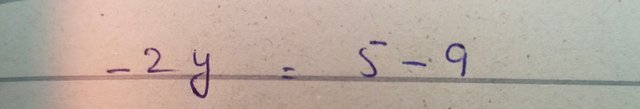
On simple substraction of we get

Step5

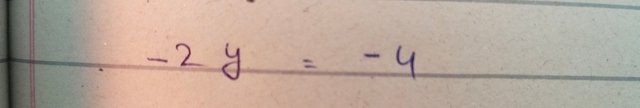
For further simplification I devide both sides with -2 . Here we get the final value of y .

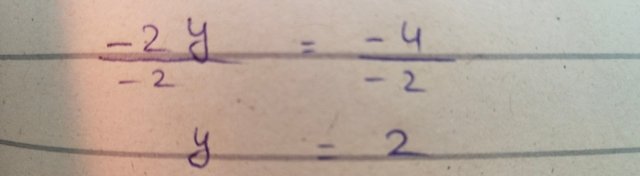
Final answer

I calculated the final answers as follow

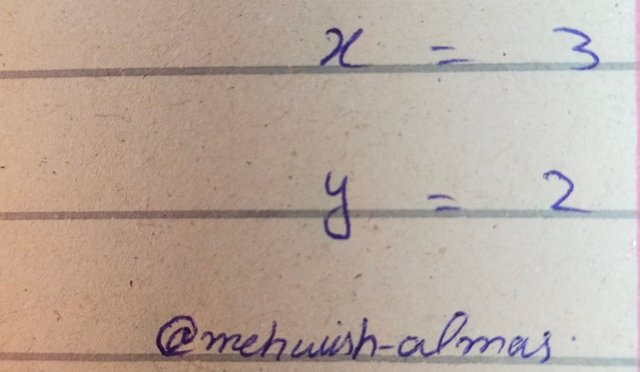
Verification:
By putting the value of variables in any of expressions ,results will satisfy both side of equations.
Here I use the equation (i)
And by putting x= 3 and y = 2 we get
3 + 2(2) = 7
3+ 4= 7
7=7

Algebraic expression (b) is

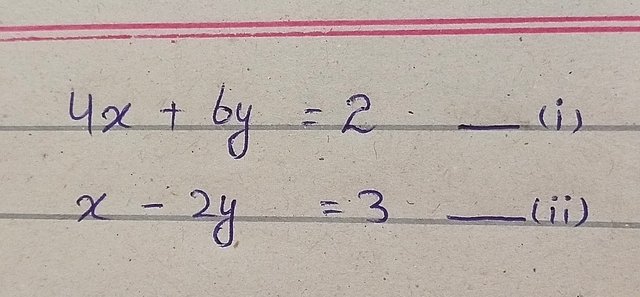
Here in this case I'm going to solve this algebraic expressions with the help of substitution method.

First of all in substitution method we calculate the value of one variable in terms of other variable. Then substitute the value of calculated variable in any of given expression and on simplification of this expression we get the value of on variable.

Step1

So in our case I took the equation (ii) to calculate the value of x in terms of y . Here I just simply rearrange the given expression and get the value of variable "x"

Step 2

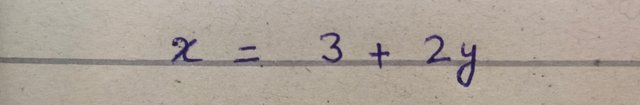
Now put the value of x in equation (i) as I shown below

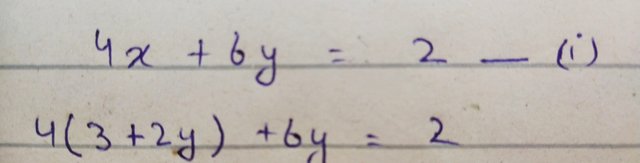
Now multiple the 4 with the terms inside parentheses I get

12+8y + 6y = 2

Step 3

Rearrange the equation to gather the similar algebraic terms

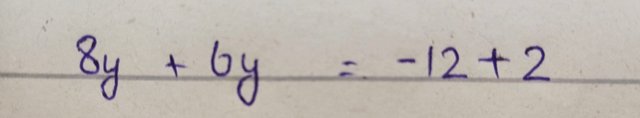
On simplification I get

Step 4

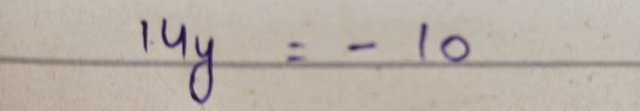
Now after dividing both side of equations with 14 we get the following expression

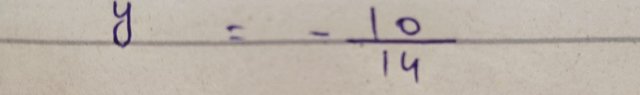
And on simplification I get the value of y variable as follow

Step 5

Now by putting the value of y in equation(ii) as follow

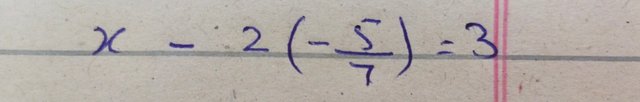
On rearranging the equation to get the value x we have given expression

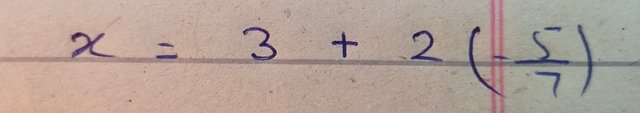
After simple multiple the above equation changed as follow

Step 6

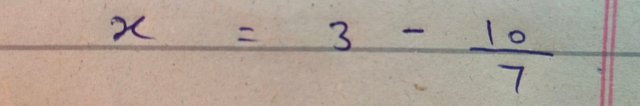
Solve the above expression by taking its L.C.M
As given below

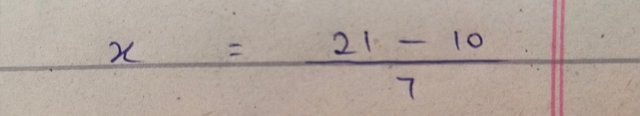
On substraction of 10 from 21 I get the value of x

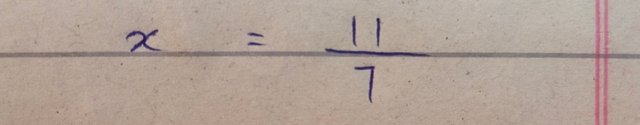
Final values of both variables are given below

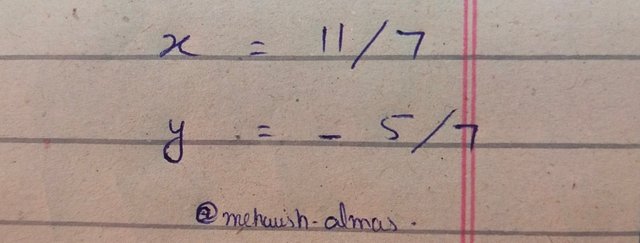
Verification:
To check the correctness of both values we can put them in any of given expressions and it satisfied both sides of equation i.e left hand side = right hand side.so put the calculated values of x and y into equation (ii)
11/7 - 2 (-5/7) =3
11/7 + 10/7=3
11+10/7=3
21/7=3
3=3

📌Task 4

Scenario # 1

Given Data

Units of product A = x = 50
Units of product B = b = ?

Equation for cost of material is 2x + 3y= 130 ...i
Equation for cost of labor is x+ 2y= 110 ....ii

Solution

(to calculate the value of product B units):

By substitution of value of x in equation (i) we can get
2(50) + 3y = 130
100 + 3y = 130 ( here 2 ×50 = 100)
Rearrange the above equation to gather like terms we can get
3y= 130-100
3y = 30
Devide both sides with 3 we get the following equation

y= 10

No put the value of x in equation (ii) we can proceed as follow
50 + 2y = 110
Rearrange the above equation to gather like terms
2y = 110-50
2y = 60
Devide both sides with 2 we get

y= 30

Here we get the two different values for y (i).e for equation i y= 10 while for equation( ii ) the value of y= 30.It reflects that in given scenario the system of equation is inconsistent.

For further confirmation we can put the values of x and y into any equation
For x=50 and y= 10
Equation (i)
2(50) +3(10)= 130
100+30= 130
130= 130

And equation (ii)
50+2(10)= 110
50 + 20= 110
70≠110
The final solution for eq( i) shows equality while (ii ) shows the different values on both sides

---

For x= 50 and y = 30
Equation (i) becomes
2(50)+3(30)=130
100+ 90= 130
190≠130 or 19≠13
And equation (ii)
50+ 2(30)= 110
50 + 60= 110
110= 110 or 11=11
In above both solution the results are not satisfied the equality in case of equation (i)

Conclusion:

So according to my perception the given system of equations is inconsistent and have no proper solution.

Scenario # 2

......

Given data

Number of vanilla= x = 30
Number of chocolate cake= y = ?

Eq for the cost of ingredients x+ 2y = 80 ...(i)
Eq for the Cost of labour 2x + y = 70 ...(ii)

Solution:

By putting the value of x into equation( i) we can proceed as follow
30 + 2y = 80
Rearrange the given equation
2y = 80 - 30 = 50
Or divided the equation by 2 on both sides

y= 25

By putting the value of x in equation (ii)
2(30) + y = 70
60 + y = 70
y = 70- 60

y = 10

We get two different values for "y" from both equations .

Verification:
For verification when I put x = 30 and y = 25 in equation (i) the solution is given as
x+ 2y = 80
30 + 2 ( 25) = 80
30 + 50 = 80
80= 80
While for equation (ii) we can proceed as follow
2x + y = 70
2(30) + 25 = 70
60 +25= 70
85≠75
The calculated values doesn't satisfied both the equations simultaneously

Similarly if we put x= 30 and y= 10 it still doesn't provide any appropriate solution

Conclusion

It reflect that the given set of equations are inconsistent which don't have any significant solution.

Here I want to add a point with respect to Task 4. In both scenarios there is no significant solution for the given systems of equations but if we note a point that in both cases the given cost is divided in two separate equation. The given 2 equations (one for labour cost and other for ingredients or material contribute in over all production) . So if we sum up both equations and then find the values of variable it gives us an appropriate solution. I solve this and give the solution in comments section of this post.

@iqrabatool34 ,@ayesha0018 and @senehasa you are invited to play with algebraic problems

Thanks @khursheedanwar for arranging these classes,it worth to read your posts and prepare assignments.