Hi friends, after reading around I am interested in participating in an amazing challenge this week. The challenge is titled: "SLC S22W1//Variables and Expressions" by sir @khursheedanwar following the contest link.

| Previously I also invited other friends such as Mr. @irawandedy, Mr @kouba01, Mr @muzack1 , and Mr @pelon53. |
|---|
| Task 1 |
|---|
| • Explain any two variables and expressions types other than that which are explained in this course. |
| *note(Practical and algebric examples are required!) |
| Here are 2 types of Expressions namely: Conditional Expressions and Ratio Expressions |
|---|
1. Conditional Expression
This expression is usually used to determine the result of a value based on a certain condition.
Here's an easy example:
You buy an item, then the item has a discount depending on the number of items. Let's say the discount is:
Buy more than 5 items, 10% discount. We must know that if we don't buy more than 5 items, then we must pay in full.
Algebraic example:
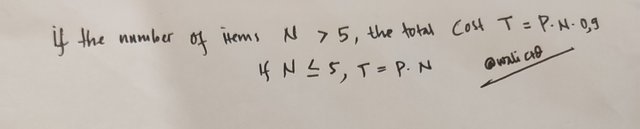
2. Ratio Expression
An expression that shows the comparison between two variables.
The practical example is :
Speed (v) is calculated as the ratio of distance (d) and time (t):
then the formula is : v=d/t
Here's an example of the problem.

| Here are 2 types of variables namely: Discrete Variables and Continuous Variables |
|---|
1. Discrete Variable
This variable has a certain value that can be calculated, but the value cannot be broken down any further.
The easy example is :
The number of students in a classroom. Let's say, X=30. Then we cannot and cannot see half the people, that's an example.
Algebraic Example:

2. Continuous Variables
In this variable, the value can change within a certain time span, so it must be a fraction as well.
The easiest example is:
In a person's weight, we say W = 65.5 kg.
Algebraic Example:

| Task 2 |
|---|
| • Show your way of evaluating of an algebraic expression if values of variables are given? Step by step explanation required! |
| *note(The more you will be detailed and accurate,the more your task will be perfect!) |
| Example 1 |
|---|

| Example 2 |
|---|

Then the following are the steps to solve it:
Substitute the values of a, b, and c into : 𝐹=(2𝑎^2)-4b+(c/2)
F=(2(2)^2) -4(3)+ (10/2)
first we have to solve the power operation first:
F=2(4)-4(3)+(10/2)
solve multiplication and division:
F=8-12+5
solve addition and subtraction:
F=8-12+5=1
So here is the final result:
F=1
| Task 3 |
|---|
| • Simplify this expression: 3(2x - 1) + 2(x + 4) - 5 |
| • Evaluate this expression: (x^2 + 2x - 3) / (x + 1) when x = 2 |
| • Solve the following equation: 2x + 5 = 3(x - 2) + 1 |
| *note(You are required to solve these problems at paper and these share clear photographs for adding a touch of your creativity and personal effort which should be marked with your username) |



| Task 4 |
|---|
| • Suppose there's a bakery selling a total of 250 loaves of bread per day. They are selling whole wheat and white bread loaves with numbers of whole wheat loaves sold being 30 more than the number of white bread loaves. If x is representing number of white bread loaves sold out and bakery is making a profit of $0.50 for each white bread loaf and $0.75 for each whole wheat loaf then please write an expression for representing bakery total daily profit. |
| • Suppose that cost of renting a car for a day is re-presented by the expression 2x + 15 and here x is the number of hours in which car is rented. If the rental company offers a package of 3x - 2 dollars for customers who take car at rent for more than 4 hours then write an expression for the total cost of renting the car for x hours and show how you simplify it. |
| *note(Solve the above scenerio based questions and share step by step that how you reach to your final outcome) |
| Bakery Total Daily Profit Equation |
|---|
Let's solve this problem:
We know total bread sold = 250 loaves.
The amount of whole wheat bread sold is 30 more than white bread.
Let us suppose that the quantity of white bread is x, then the quantity of whole wheat bread is x+30.
Meanwhile Profit:
White bread = $0.50 per loaf.
Whole wheat bread = $0.75 per loaf.

Steps we will take:
First we need to correlate the amount of white and whole wheat bread:
While we know that the total bread sold is 250 loaves:
x+(x+30)=250Next we need to solve to find x:
2x+30=250
2x=250-30
2x=220
x=110
So, since we already know the number of white loaves sold is 110, we will find the number of whole wheat loaves which is :
= x+30
=110+30
=140
- So next we will solve the equation for total profit:
Total Profit = 0.50x+0.75(x+30)
- We also need to simplify the equation:
Total Profit=0.50x+0.75x+22.50
Total Profit=1.25x+22.50
And the result is The equation for daily total profit is:
Total Profit=1.25x+22.50
| We will solve the Car Rental Cost Equation |
|---|
Known from the problem:
- Rental cost for a day: 2x+15, where x is the number of rental hours.
- Package for customers who rent for more than 4 hours: 3x-2.
- Find the equation for the total rental fee.

Here are the steps to solve it:
First we need to combine 2 scenarios in one equation:
- suppose x≤4: Cost = 2x+15.
- suppose x>4: Cost = 3x-2.
We will write it as a piecewise equation:
Total Cost={ 2x+15 if x≤4, {3x-2 if x>4
We will give a simplified example for x>4:
Substitute x=6 (e.g. 6 hours):
Cost=3(6)-2=18-2=16We will give a simplified example for x≤4:
Substitute x=3 (e.g. 3 hours):
Biaya=2(3)+15=6+15=21
Final Result:
Equation for the total cost of car rental:
Total Cost= { 2x+15 if x≤4, 3x-2 if x>4
This is the exercise I did by following the material provided by the teacher, hopefully it can be conveyed well and also useful for others. Thank you for your attention and apologize if there are any mistakes.
@walictd

https://x.com/walictd/status/1870136761327972805
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit