SLC-S22W4//Linear and Quadratic equations equations.

Hi friends, after reading around I am interested in participating in an amazing challenge this week. The challenge is titled: "SLC-S22W4//Linear and Quadratic equations equations." by sir @khursheedanwar following the contest link.

Edit by Canva

Previously I also invited other friends such as Mr. @abialfatih, Mr @kouba01, Mr @muzack1 , and Mr @pelon53.

Task 1

In this first task, let's find out what Linear Equations and Quadratic Equations are with simple examples that are clear and complete.
1. Linear Equation
A linear equation is one of the equations whose variable is only a power of 1, and only produces a graph like a straight line without curving.
We will see below one of the general forms of this linear equation:

• Suppose the linear equation has only one variable, so the general form is like this: ax + b = 0.
• However, it is different if the equation has two variables, so the general form becomes like: ax + by + c = 0
  Here is one simple example: 2x + 3 = 7
  Then the solution to the problem is:
  2x = 7 - 3
  2x = 4
  x = 2

The 2nd simple example of a System of Linear Equations that has Two Variables is :
x + y = 5 ..........................(Equation 1)
x - y = 1 ...........................(Equation 2)
Here are some steps for solving the above equation:

• Based on Equation 2, namely
  x - y = 1 becomes x = y + 1
• Next let's substitute x = y + 1 into Equation 1 i.e.
  x + y = 5 ..................................... Enter the value of x = y + 1, so it looks like :
  (y + 1) + y = 5
  2y + 1 = 5
  2y = 4
  y = 2.
• Next, let's substitute y = 2 into equation 2, x = y + 1:
  x = 2 + 1 = 3
• The end result is x = 3 and y = 2

2. Quadratic Equation
Different from linear equations, because we need to know that what is meant by a quadratic equation is one of the equations in which there is a variable of the 2nd power, and the graph of this equation is parabolic.
While the general form is also very different from linear equations, in quadratic equations the general form of a quadratic equation is:
ax^2 + bx + c = 0
To make it easier to understand, please see the example problem:
x^2 - 4x + 3 = 0
In solving the above problem, we need to use factorization:

• The first step is the factorization as below:
  x^2 - 4x + 3 = 0 so that after factoring it becomes (x - 3) (x - 1) = 0
• After factoring it, we will know the result:
  x = 3 or x = 1

If one example isn't enough, let's look at a simple example of the 2nd System of Quadratic Equations:
x^2 + y = 10 ....................(Equation 1)
y = x + 2............................(Equation 2)
Here are the solution steps:

• We need to insert y = x + 2 from equation 2 into equation 1: i.e. x^2 + y = 10
  x^2 + y = 10
  x^2 + (x + 2) = 10 ................................(After substitution)
  x^2 + x + 2 = 10
  x^2 + x - 8 = 0.

• Next let's factorize:
  x^2 + x - 8 = 0.

  (x + 4)(x - 2) = 0
  After factoring, we know that it is x = -4 or x = 2.

• Let's find y for each x:
  If x = -4, then the result is y = x + 2 = -4 + 2 = -2.
  Meanwhile, if x = 2, then the result is y = x + 2 = 2 + 2 = 4.

• The final result is :
  (-4, -2) and (2, 4).

Here is a table of the main differences between linear equations and quadratic equations:

Task ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ 2

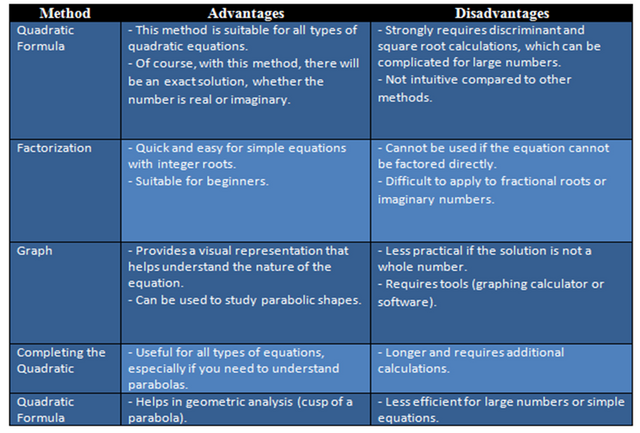
There are many methods to use in order to solve quadratic equations, but this time I will share a few of them, including:

1. Using the Quadratic Formula or better known as the ABC Formula.

Maybe we all know that the ABC Formula is one of the most versatile methods for the reason that this method can also be used so that all types of quadratic equations, both those with integer and fractional roots. The ABC formula is :

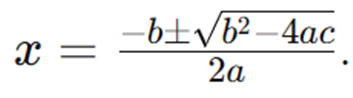
Friends, let's look at a simple example of a quadratic equation and we will solve it using the formula above. For example, there is a problem with an equation that is : x^2 + 2x - 8 = 0. So we immediately identify that a = 1, b = 2, and c = -8. After that, we will calculate the discriminant with the formula above: ((b^2) - (4ac)) so the value is 2^2 - 4(1)(-8) = 4 + 32 = 36.
Let's put it into the ABC formula, so it will be as follows:

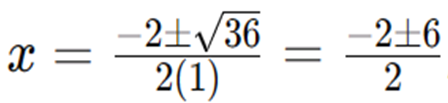
Solve for both possibilities (+ and -)
X= (-2+6)/2= 4/2=2
X=(-2-6)/2=-8/2=-4

So the result :
x = 2 or x = -4.

2. Using the factorization method

Generally, we use the factorization method when the roots of the equation are integers. To make it easier to understand, look at the example of the equation.
x^2 - 5x + 6 = 0
The first step we just need to find two numbers that can be multiplied by 6 and the sum is -5, then the numbers are -3 and -2.

So, the equation is factored into :
x^2 - 5x + 6 = 0 --------------------> (x - 3)(x - 2) = 0
Result :
x = 3 or x = 2.

3. Using the Graph method

When using the graphing method, it will of course involve drawing a parabola of the quadratic equation and finding its intersection point with the x-axis.
Let's look at a simple example of the following equation
x^2 - 4 = 0
then we can find that the graph will intersect the x-axis at x = -2 and x = 2.

4. Using the method of completing the Square

With this method, we need to convert the equation into a perfect square form. To make it easier let's look at a simple example:
x^2 + 6x - 7 = 0
first we need to move the constant so it becomes :
x^2 + 6x = 7
We need to add (6/2)^2 = 9 to both sides of it so it becomes :
x^2 + 6x + 9 = 16
Next we will root it, we get the result :
x + 3 = ± 4
so the result : x = 1 or x = -7.

Task 3

Task 4

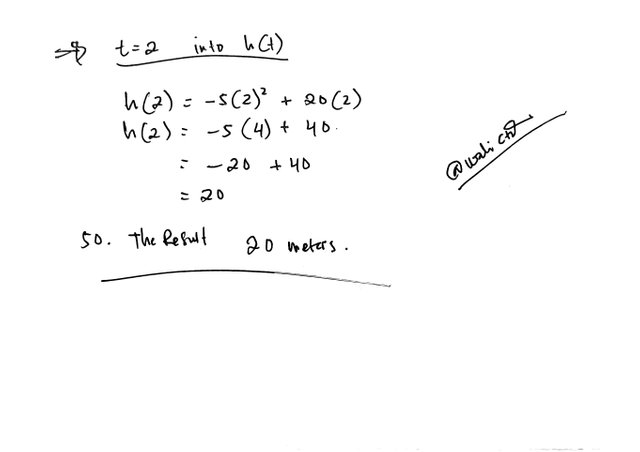
This is the exercise I did by following the material provided by the teacher, hopefully it can be conveyed well and also useful for others. Thank you for your attention and apologize if there are any mistakes.

Best Regard
@walictd