
¿Qué es la Programación?
La programación de computadoras (a menudo abreviado como programación o codificación) es el proceso de diseñar escribir, probar, depurar y mantener el código fuente de los programas de computadoras. Este código fuente está escrito en uno o más lenguajes de programación.
El propósito de la programación es crear un conjunto de instrucciones que utilizan los computadores para realizar operaciones específicas o para exhibir comportamientos deseados.

¿Qué es un Algoritmo?
En matemáticas y ciencias de la computación, un algoritmo (del griego y latín, dixit algorithmus, arithmos, que significa número, introducción de este término, gracias al matemático Abu Abdallah Muhammad ibn Mūsā al-Jwārizmī (Abu Yāffar), mejor conocido como Al-Juarismi) es un procedimiento paso a paso para calcular algo, procesar datos y realizar un razonamiento automatizado.
Más precisamente, un algoritmo es un método eficaz expresado como una lista finita de instrucciones bien definidas para el cálculo de una tarea.

Los inicios de la computadora



“Es indigno de los hombres excelentes perder horas como esclavos en el trabajo del cálculo que podían ser relegados sin peligro a alguien más si las máquinas fueran usadas.”

Sistemas de Numeración
Los sistemas de numeración, nos permite a través de un conjunto de símbolos (pueden ser dígitos numéricos y o letras, o cualquier otro tipo de carácter) y una lista de reglas para su combinación y uso de los símbolos, que permitirá construir los números del sistema. Así lo podemos escribir de manera formal, como sigue:

donde
Los sistemas de numeración más comunes son el sistema decimal (es el que usamos a diario), el sistema binario (es el sistema que usan los computadores, también conocido como lenguaje máquina), el sistema octal y el sistema hexadecimal.
En general, la regla para describir un sistema de numeración podemos enunciarla de la siguiente manera:

Adicionalmente, como ya mencionamos el sistema binario, el cual consta de solo dos símbolos,
Por ejemplo, se deseamos especificar la base en la que está definido un número, se utiliza el índice en la parte inferior derecha del número:

lo cual nos indica que el número esta definido en un sistema de numeración en base 2, o comúnmente llamado binario. De igual manera si tenemos el número

nos indica que el número está definido en un sistema de numeración en base 8, o comúnmente llamado octal.
Cuando tenemos por ejemplo un número en el sistema decimal, es normal omitir el índice 10, sin embargo el mismo se utiliza solo en los casos que sea necesario aclarar el concepto. La palabra dígito se refiere generalmente a los símbolos del sistema decimal, pero también lo usaremos para designar los de los demás sistemas con este mismo nombre.

Sistema Posicional
Ahora bien, los sistemas numeración que hemos considerado por ahora, incluido el sistema decimal, están basados en los sistemas posicionales, esto quiere decir, que un el valor de un símbolo en un número de el sistema, tiene una represerntación que depende unicamente de la posición que ocupe dicho número. Veamos un pequeño ejemplo en el caso de números en el sistema decimal:

el dígito 7, representa 700 unidades en el número 725; mientras que el mismo dígito 7 representa 70 unidades en el número 571. Lo podemos ver visualmente de la siguiente manera:
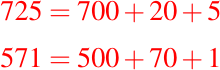
Así que podemos generalizarlo de la siguiente manera:
- Se numeran los dígitos de derecha a izquierda con un superíndice, empezando desde cero, e incrementando de uno en uno en los dígitos de derecha a izquierda. Por ejemplo:
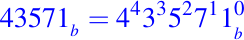
- Luego, cada superíndice de cada dígito se utiliza para escribirlo en forma de potencia de la base del sistema de numeración donde estemos expresando la representación numérica. Por ejemplo,

- Posteriormente, se multiplica el valor del dígito, por su potencia de la base correspondiente.
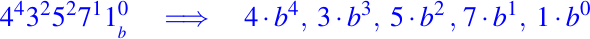
Ahora, si deseamos conocer el equivalente en el sistema de numeración decimal del número entero dado, sumamos todos los productos obtenidos en el paso 3.
Veamos algunos ejemplos donde podremos aclarar mejor lo que acabamos de enunciar.
Ejemplo 1. ¿Cuál es el valor de cada dígito en el número 3275 en el sistema de numeración decimal ?
La base del sistema de numeración decimal es 10. Así que para obtener el valor de cada dígito debemos seguir los pasos mencionado anteriormente como sigue:
- Numeramos los dígitos usando superíndices. Entonces, el número se puede escribir de la siguiente manera:
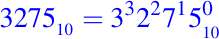
- Tomamos los superíndices para formar potencias de la base de la siguiente manera:
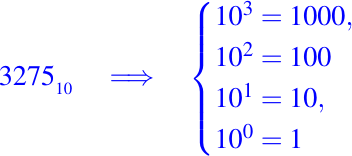
- Multiplicamos cada dígito por las potencias correspondientes:
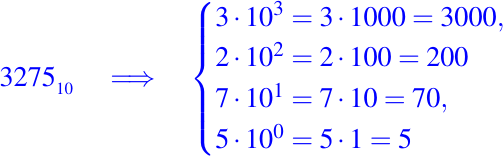
Ejemplo 2. ¿Cuál es el valor de cada dígito en el número 3275 en la base octal? ¿Cuál es el equivalente decimal del número?
Como la base del sistema de numeración es la octal, entonces la base es 8. Siguiendo el algoritmo dado anteriormente tenemos lo siguiente:
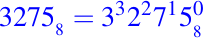
Luego tenemos:
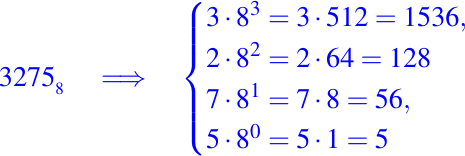
Así, su equivalente en el sistema de numeración decimal se obtiene sumando todos los productos que ya obtuvimos previamente:
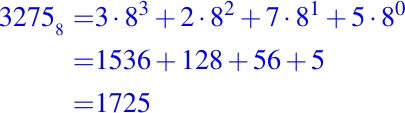
Podemos observar que cada vez que hacemos la equivalencia de número en el sistema de numeración decimal, también determinamos el valor individual de cada dígito en el sistema de numeración decimal.

Queridos amigos y lectores, espero hayan disfrutado de este primer punto de la serie de Computación y Programación, los espero en la próxima entrega de esta serie, donde continuaremos hablando de los sistemas de numeración y otras cosas interesantes. Espero que esto pueda servir de apoyo a ustedes, hijos, nietos, sobrinos o amigos que quieran aprender un poco mas del maravilloso mundo de las matemáticas y la computación. No olviden dejar sus comentarios. Saludos y nos leemos pronto.
Si desean consultar un poco más del tema pueden usar las siguientes referencias.
- Knuth, Donald Ervin. The art of computer programming. Vol. 1, 2, y 3. Pearson Education, 1997.
- Knuth, Donald Ervin. Fundamental algorithms: the art of computer programming. 1973.
- Knuth, Donald Ervin. Computer programming as an art. ACM Turing award lectures. ACM, 2007.
Todas las ecuaciones fueron creadas y editadas por @abdulmath con
 , y GIMP.
, y GIMP.

Imagen elaborada por @abdulmath, diseñadas y editada con Karbon y GIMP.
La base matemática que nos llevará a dominar los conceptos de programación..! ¡Votado por Engranaje!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Muchísimas gracias por el apoyo. Saludos y un abrazo a todo el equipo.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Saludos @abdulmath.
Interesante post. Noto que desarrollas algunas nociones de diferentes temas en un sólo post, tales como 1) programación, 2) historia del computador y 3) sistemas de numeración.
Tengo una pequeña observación 😉. El apellido del matemático es "Turing", no "Touring", el autor de la "Máquina de Turing", que mencionas, que por cierto, no es una máquina mecánica o electrónica como tal, sino abstracta. Un modelo computacional, para ser más exacto.
Buen post. Éxito!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Hola @eniolw, gracias por tomar el tiempo y leer el post.
Como mencionas que toco tres temas diferentes, quiero aclarar que no lo hago a profundidad, solo hago mención a manera de introducción, pues es importante entrar en contexto para lo que se desarrollara a futuro. El error en el apellido fue un exceso de teclado, se me paso la letra. La maquina de turing es un concepto abstracto pero que se construyó una maquina basado en ese concepto abstracto.
Gracias de igual manera, por tus comentarios.
Saludos y un abrazo!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Felicitaciones por tan completo y hermoso trabajo.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Hola @carlucmeza, gracias por tus comentarios. Saludos
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Esta muy buena la información. Excelente. Felicitaciones
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Hola @analis69, gracias por tus comentarios, y gracias por las felicitaciones! Saludos y un abrazo.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Como siempre nos traes una clase magistral. Felicitaciones
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Hola, que bueno que te gustará mi post. Saludos y un abrazo.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
hola hermano como estas?
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Hola @duque, todo bien gracias! Y tú cómo estás? Saludos
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Hola gracias por tus comentarios, saludos y un abrazo.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Excelente esquematización sobre programación y diseño de algoritmos, además de didáctica las explicaciones dadas. Saludos amigo @abdulmath.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Hola @lupafilotaxia, nuevamente agradezco tus comentarios. Es bueno leer que se entiende el tema. Seguiremos trabajando. Saludos y un abrazo.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Saludos @abdulmath, muy bueno tu post, conceptos viejos de mi carrera que aún mantengo en mi memoria RAM y ROM de manera muy activa.
Aunque no soy de la época de ábaco y de las tarjetas perforadas sino desde W95 y Canaima jajajaja, excelente post
Un Abrazo.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
hola @henjos, di la verdad, tu eres de la época de windows 3.1 y MS-DOS, jajajajajaja Saludos y gracias por leer mis publicaciones y compartir tus vivencias. Un abrazo.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Muy buen articulo compañero Abdul!! gracias ;);)
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
hola @adri525, gracias por tu comentario. Saludos.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit