
¿Quién sabe? En algún momento podemos sacarle provecho; ¡Todo conocimiento es poder!
Ahora bien, como ya sabemos el sistema binario es el más utilizado, ya verán la razón de esta afirmación. Encontraran en este artículo:
- Representación de Cantidades
- Métodos.
- Ejemplos.
Conversión de Decimal a Binario
Existen dos maneras de convertir un numero decimal a su representación equivalente en el sistema binario: La primera bajo la forma de una suma de potencias y La segunda bajo el método llamado "Método de las Divisiones Sucesivas entre Dos".
A manera de mostrarles con facilidad las conversiones iniciare con un ejemplo para describirles el proceso a realizar.
1. Suma de Potencias
| 2^6 | 2^5 | 2^4 | 2^3 | 2^2 | 2^1 | 2^0 |
| 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 0 | 1 | 1 | 0 | 1 |
Procederemos aplicando estos pasos hasta que el valor se reduzca a " 0 ".
Cada potencia que usemos en este proceso, en el sistema Binario, será representada por el valor " 1 ", las que no estarán representadas por el valor " 0 ".
Después de terminada la conversión tenemos que 45 = 101101
2.Método de las Divisiones Sucesivas entre Dos
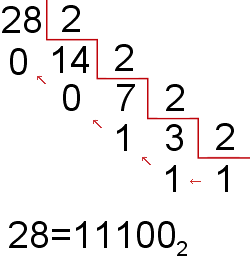
Conversión de Binario a Decimal
| 1 | 1 | 0 | 1 | 1 |
| 2^4 | 2^3 | 2^2 | 2^1 | 2^0 |
| 16 | 8 | - | 2 | 1 |
Si tomamos los valores, 16 + 8 + 2 + 1 y los sumamos tendremos como resultado la conversión del numero binario 11011 = 27.
Ya somos unos expertos en la conversión Binario - Decimal; Decimal - Binario.
Recuerda seguir los posts que siguen, vienen con más contenido instructivo.
Esta super bueno el post para mostrarselo a mi hija que justamente está viendo esto en el cole, gracias por compatirlo, saludos y te invito a pasar por mi blog @maleudi y ver mi última publicación sobre una caminata de 42K por un camino muy lindo y boscoso, ya me contarás que te pareció... Saludos y aquí tienes una seguidora más...
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Muchas gracias, espero que le saques provecho. Saludos
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Muy pero muy bueno tu post, excelente.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Información realmente útil. Excelente explicación. Gracias por compartir.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
El conocimiento es poder, que bueno disfrutaras el artículo. Saludos
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit