Original Image Source
Introduction
This series of posts seeks to present the material covered in the first semester of a college level general chemistry course, in an easily digestible steemit blog post format. The series is intended to be read, and experienced in sequential order starting with Post 1. The material will build upon itself, and potential exercises included (problem sets), will pertain to the post they are contained in, or any previous post. Each post will pick up immediately where the previous in the series left off. Please check out the #chemistry-lesson tag for all posts in this series. I hope you find this series to be informative and beneficial toward your understanding of chemistry and science in general.
Immediate Preceding Post
Part 8: Gasses and Reactions in the Gas Phase 1
Legend for This Section
As subscripts do not currently work on steemit, to symbolize when a number should be sub-scripted I will be writing it in the text as follows: /x/.
To facilitate the inclusion of subscripts and styling of equations used for examples and for ease of the inclusion of equations a combination of MS word and image editing programs are used. All examples and equations included in these posts are generated by my own hands. NO photocopies of any outside material are used.
Partial Pressures
In the previous post from this series we began to learn how to deal with reactions taking place in the gaseous phase. We learned about the ideal gas equation:
Recall that P is pressure, V is volume, n is number of moles of the gas, R is the gas constant (defines as 0.08206 (L•atm)/(K•mol)) and T is the temperature in Kelvin. We applied these equations to determine the amounts of a pure substance. However as we all know most of the time we aren’t dealing with a pure substance but rather a mixture. Today we begin by discussing partial pressures. Partial pressures are the terms given to the gaseous pressures of individual component gasses in a mixture. There is a scientific law dealing with the pressures of individual gasses called Dalton’s law of partial pressures. What Dalton found was that the total pressure of a mixture of several gasses is just the sum of the pressures that each of those gasses would place on their container. Source
This means that Total P = P1 + P2 + P3 …. For as many gasses as are in the mixture. We can use this idea and think about these pressures in terms of the ideal gas law:

Where the greek letter chi (χ) means mole fraction aka… the ratio of the moles of the individual gas over total number of moles of gas. At this point you are likely scratching your head saying “yeah that’s a bunch of algebra, why do I care?” (…or perhaps you gave up already I HOPE NOT!!) Well let me tell you why WE care, it’s because this makes partial pressures super easy to determine! Now if we have a mixture of gasses and want to figure out the pressure from one component (gas X) we do the following:
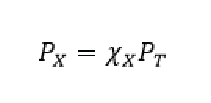
Meaning that the partial pressure of gas X is equal to the ratio of the number of moles multiplied by the total pressure. Lets go through an example of calculating a partial pressure:
A mixture of gasses contains 7.3 moles argon (Ar), 1.5 moles Neon (Ne), 3 moles oxygen (O2) and 5 moles Helium (He). The total pressure at a specific unspecified temperature is 74 atm. What is the partial pressure of Neon?

Simple Kinetic Theory for Ideal Gasses
So now we have described the gas laws and can do a pretty good job predicting some of the properties a sample of gasses will have. However our ideal gas law equations do not tell us anything about what is happening at the molecular level of gasses. For instance, why do gasses expand? Why does temperature influence the properties of gasses described in the ideal gas law? To answer these questions we must dive a bit into the motion of gas molecules. Kinetic Energy is defined as “energy that a body possesses by virtue of being in motion.” (Source) so when we talk about the kinetic theory for gasses we are really discussing the motion of gaseous atoms. The kinetic theory of gasses has a few basic assumptions:
Gasses are made up of molecules and separated by distances larger than their own dimensions. As such a gas molecule can be considered a point, meaning that while it has a mass, its volume is negligible.
Gas molecules are constantly moving in all directions randomly. They frequently collide with one another but these collisions are perfectly elastic, meaning that energy can be transferred perfectly from one molecule to another resultant from the collision. However the total energy of all molecules in the system remains the same regardless of the number of collisions. Or in other words energy is not lost through any sort of radiative process as a result of the collisions between gas molecules.
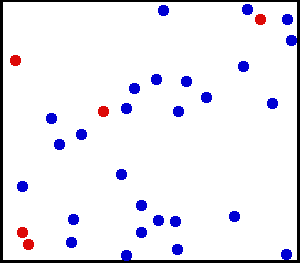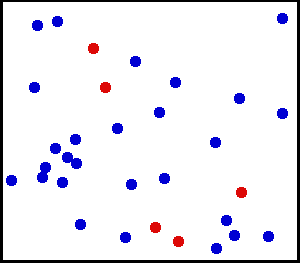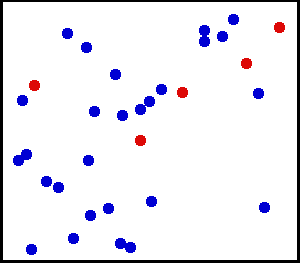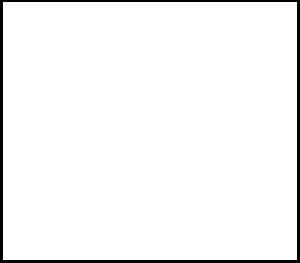
You can watch in the gif above how this works by following the red atoms. They move around and get smacked into by the blue atoms. Sometimes they stall and transfer their energy to a blue atom, and other times they quickly move as the energy from a blue atom is transferred to them. Despite this, total energy in that box remains constant.
Gas molecules do not attract or repel one another in any way.
The average kinetic energy of a gas is proportional to the temperature of the gas in Kelvin. The equation to determine average kinetic energy of a molecule is:
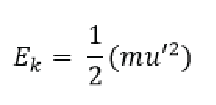
Where m is the mass of the gas molecule and u’ is its average speed. Since the law assumes that the Kinetic Energy E/k/ is proportional to temperature we can replace Kinetic Energy in the equation above and replace it by temperature:
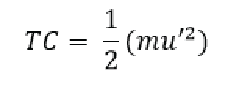
So now we have Temperature (T) times a proportionality constant C (as it’s not directly equal to temperature but some ratio, this C accounts for that ratio) is equal to one half the sum of the mass of the gas molecule multiplied by the square of its average speed.
(A brief apology to the physicists) This is a very simplistic view on gasses and the assumptions are overly strict. A significant amount of work has been done to understand gasses and there is A LOT more detail that can be gone into. However for this brief introduction from a general chemistry perspective this is as detailed as we will get. I have provided a few links for further reading if you are so inclined:
Additional Information
Additional Information 2
How does this change our understanding of the gas laws from the previous post?
Since gasses molecules are separated by very large spaces, we now know that gasses can be compressed quite easily and forced to occupy small volumes. This also explains why pressure rises as the volume of a container is reduced. Smaller volume means a higher density of gas molecules all making contact with the walls of the container. These collisions are what result in pressure, so more collisions means more pressure. We also see how temperature influences that pressure, since temperature is directly proportional to kinetic energy, heating a gas leads to more molecules being able to collide with the walls of their containing vessel. Similarly to the previous observations, more collisions again results in more pressure.
How Fast Does A Gas Molecule Move Anyway?
We will end this section with a discussion on root mean square speed (RMS), which is just average molecular speed. Because of the kinetic theory of gasses we can state that the total kinetic energy for 1 mol of a gas is equal to (2/3)RT where R is the gas constant and T is temperature in kelvin. We can combine this with our previous equation for an individual gas molecule to get the following:
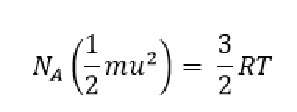
Here N/A/ is avogadros number (as remember we said that 2/3 RT is for a mole of a gas and Avogadros number is the number of individual molecules in one mol. We can do a bit of algebra and simplify things to say that:
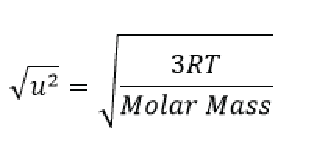
We can then use this equation to calculate the speed of gas molecules! To do so we must use a different gas constant (8.314 J/K mol)… So let’s do one last example.
What is the rms speed of an oxygen molecule at 298K (298 K is equivalent to 25 °C if you recall)? Note that 1 J = 1 kg m2/sec2.

Here we have plugged the values into the rms equation including the gas constant R, the provided temperature in K and the molar mass of oxygen, since oxygen is diatomic we have multiplied its molecular mass from the periodic table by 2. We find that an O/2/ molecule moves at an average of 481 meters per second! That’s fast!
I hope this post has given you a little bit of increased knowledge about gasses, and how we can use a variety of mathematical equations and approximations to know things about their properties!
Future Posts
Subsequent posts will cover: Electronic Configuration of Atoms, Chemical Bonding, and Molecular Geometry, and more.
Reference Figure: Periodic Table
Other References
Constants and Conversions List
Source for Additional Constants
Some Common Ions
An Open Source Chemistry Text Book
Additional Sourcing Information
General Chemistry: Principles, Patterns, and Applications
General Chemistry: The Essential Concepts
General Chemistry
If you like my work, please consider giving me a follow: @justtryme90. I am a PhD holding biochemist with a love for science. My future science blog posts will cover a range of topics in the biology/chemistry fields.
Thank you for your support of my work!
Apologies accepted (this was to easy ... I am almost sure you did it on purpose :p ). I have no question/comment this time :)
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
I love Chemistry too! :)
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
You're awesome @virtualgrowth, I hope you know that.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Not me, I'm just me. Live, the universe, and everything is full of awesome-ness.


The more one lets be, the more one is to be!
Awesome is just a risk worth taking!
source: zubeezone.com
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Edited to include an explanatory section/disclaimer regarding how examples are generated for these posts. To work around the lack of subscripts and more advanced equation editing in the blogging platform a combination of MS word and Illustrator are used to make the equations and save them in a format for hosting on an image host. For examples with multiple equations necessary, I even include descriptive text between the images all as one large image, rather than hosting 5 separate images for each equation.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Bravo! another brilliant post, it discusses the physics and chemistry in a simple way, thank you very much congratulations
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Thank you for your kind words! More to come, will keep at this. Lots of fun topics to discuss coming up!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Well organized and a great lesson. You are putting a lot of effort into your posts and a big thanks for posting high quality content!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Thank you for reading!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit