下面是某银行的一个存款数据样本,自变量是年份,有四个应变量。
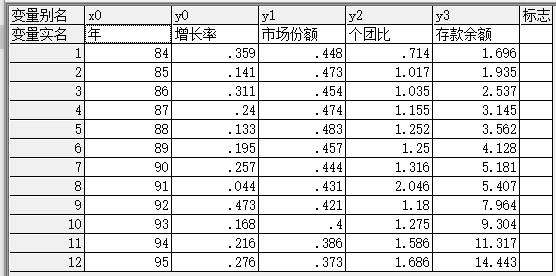 图 5.1. 一元多响应数据样本
图 5.1. 一元多响应数据样本
我们分别把这些数据描绘在坐标图上,这样管理数据是不是很有意思呢?但是,如果把数据点绘在图上会更清楚,更直观,更一目了然。
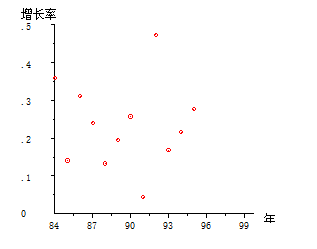
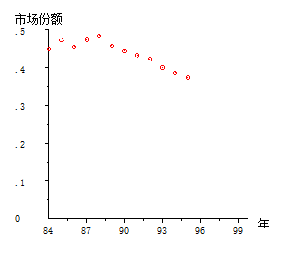
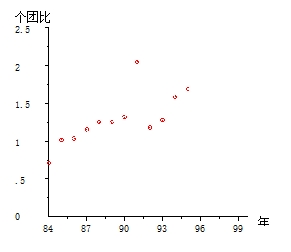
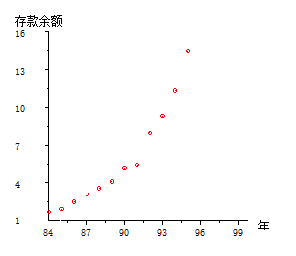 图 5.2. 点绘
图 5.2. 点绘
作为管理者品尝和咀嚼这些数据,一定会有所思考,有所发现,会产生某些改进管理的冲动。首先看看年增长率,我们把这些点作简单的连接。折线起伏波动巨大,波涛汹涌,大船的驾驶者费尽力气,难以驾驭。对这些数据,用一根直线来拟合几乎没有指导意义。
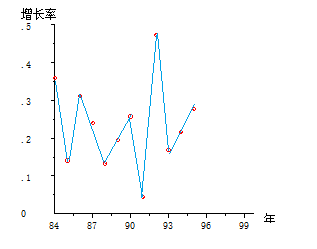 图 5.3. 年增长率分析
图 5.3. 年增长率分析
再看市场占有率,搏击到 89 年,可谓直线上升,而后逐年直线下降。全程用一根直线来拟合显然不合适。而应该以89年为界,分段拟合。89 年之后直线下滑,管理者是不是该找找原因呢?
个人存款较团体存款之比逐年递增,以92年为甚。93年大幅下跌。随后趋稳。应该说主要由政策和社会因素所决定。关于这些问题,经济学家会有很好的解释,脱离了我们的主题,不加赘述。
下面我们重点讨论存款余额的增长分析于预测。由图 4 和图 5,可以看出,线性拟合的效果也是不错的。
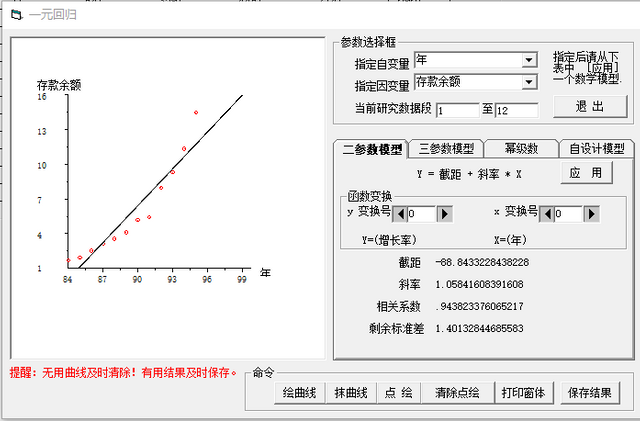 图 5.4. 线性拟合存款余额
图 5.4. 线性拟合存款余额
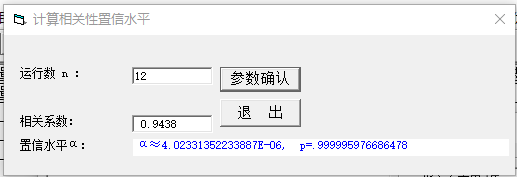 图 5.5. 线性拟合存款余额的置信概率
但是,点排列在一条很光滑的曲线上。用曲线拟合会更好。应该用什么样的曲线拟合比较好呢?程序具有抹除现有直(曲)线,提供了许多可供拟合的模型,可以选择某条曲线尝试进行拟合比较。在这里,自由度相同,我们只需比较相关系数就可以了。下面择取两条展示这种操作。
图 5.5. 线性拟合存款余额的置信概率
但是,点排列在一条很光滑的曲线上。用曲线拟合会更好。应该用什么样的曲线拟合比较好呢?程序具有抹除现有直(曲)线,提供了许多可供拟合的模型,可以选择某条曲线尝试进行拟合比较。在这里,自由度相同,我们只需比较相关系数就可以了。下面择取两条展示这种操作。
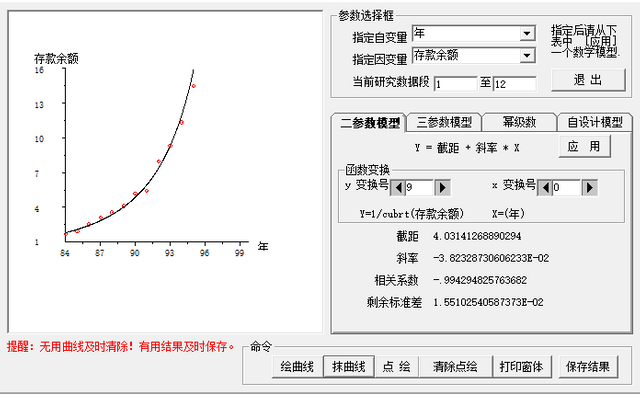 图 5.6. 第一种非线性拟合存款余额
图 5.6. 第一种非线性拟合存款余额
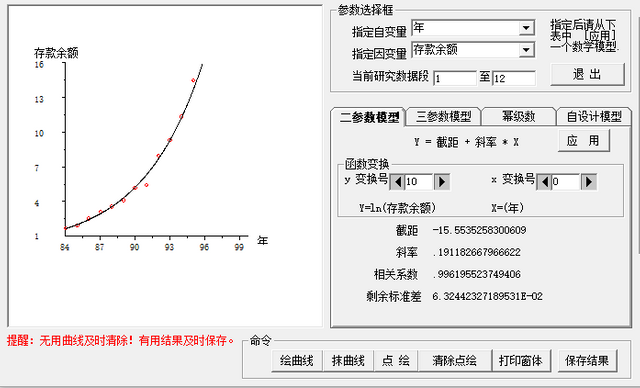 图 5.7. 第二种非线性拟合存款余额
图 5.7. 第二种非线性拟合存款余额
这两种拟合都很好。关于这些曲线的函数形式我们下节介绍,图 5.7 的拟合相关系数更高。
但是,图 5.6, 图 5.7 哪个的预报更准?对于趋势的预测,二者都可以供参考。
由以上操作可以看出,非线性拟合看上去很容易。如果不是由计算机辅助,可就很难。关于非线性回归的数学描述,下节介绍。
参 考
- 茆诗松,丁元,周纪芗,吕乃刚编著,《回归分析及其试验设计》,华东师范大学出版社,上海,1981
- George.E.P.Box, J.Stuart Hunter, William G.Hunter, Statistics for Experimenters (Second Edition),2005
- T.Hastie,R.Tibshirani,J.Friedman, The Elements of Statistical learning, Springer-Verlag,New York,2001
- J.S.Milton, Jesse C.Arnold, Introduction To Probability and Statistics,(Third Edition ),1995









