Álgebra de Conjuntos en Sagemath

Dentro de los conjuntos existen operaciones básicas para trabajar con ellos. En las lineas siguientes mostraremos su definición y como calcularlos en sagemath

Unión: $A\bigcup B$

Es el conjunto formado por los elementos que están por lo menos en uno de ellos.

Ejemplo 1:

$A= \left \{ 1,2,4 \right \} \\ B= \left \{ 3,4,5 \right \} \\ A\bigcup B=\left \{ 1,2,3,4,5 \right \} \\$

En Sage:

A=set([1,2,4]) B=set([3,4,5]) C=A.union(B) C

Intersección: $A\bigcap B$

Este conjunto esta formado por los elemento conjuntos de A y B

Ejemplo 2:

$A= \left \{ 1,2,4 \right \} \\ B= \left \{ 3,4,5 \right \} \\ A\bigcap B=\left \{ 4 \right \} \\$

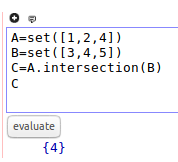
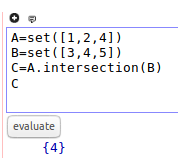
A=set([1,2,4]) B=set([3,4,5]) C=A.intersection(B) C

alt

Diferencia: $A \setminus B$

Son los elementos de A que no estan en B

Ejemplo 3:

A=set([1,2,4]) B=set([3,4,5]) C=A-B C

alt

Diferencia simétrica $A\Delta B$

Son todos los elementos que pertenecen, o bien a A, o bien a B, pero no a ambos a la vez

Ejemplo 4:

$A= \left \{ 1,2,4 \right \} \\ B= \left \{ 3,4,5 \right \} \\ A\Delta B=\left \{ 1,2,3,5 \right \} \\$

alt

Posted from my blog with SteemPress : https://matematicapositiva.com.ve/algebra-de-conjuntos-en-sagemath/