Leslie Lamport proposed in 1982 a fictitious model to explain the consistency problem.
Byzantium was the capital of the ancient Eastern Roman Empire. Due to its vast territory, multiple generals (multiple nodes in the system) guarding the border needed to send messages through messengers and reach certain unanimous decisions. However, because there may be traitors in the generals (the nodes in the system go wrong), these traitors will try to send different messages to different generals, trying to interfere with the agreement.
The Byzantine problem is how to get loyal generals to reach a consensus in this situation.
For the Byzantine problem, if the total number of generals is N and the number of rebellious generals is F, the problem will be solved when N>=3F+1, that is, when the rebellious generals do not exceed 1/3, there is an effective algorithm, such as BFT, no matter how the mutineers toss, the loyal generals can always reach a consensus.
This is the conclusion of a mathematical argument, and interested students can deduce it by themselves.
PBFT An efficient Byzantine fault-tolerant consensus algorithm
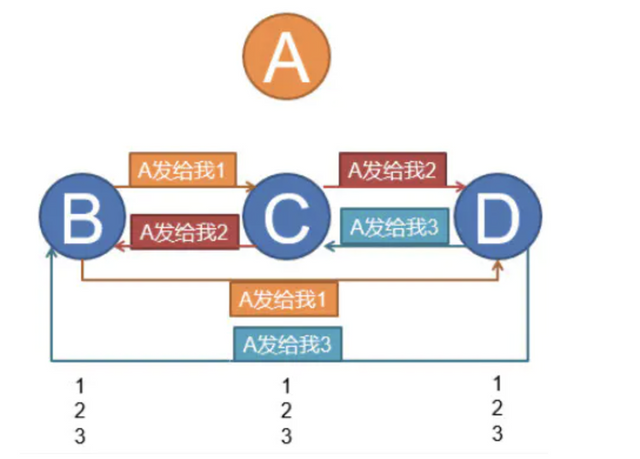
PBFT is the abbreviation of Practical Byzantine Fault Tolerance, which means practical Byzantine Fault Tolerance algorithm. This algorithm was proposed by Miguel Castro and Barbara Liskov (2008 Turing Award winner) in 1999, and it solved the problem of low efficiency of the original Byzantine fault-tolerant algorithm.
His core idea is: For every general who receives an order, he must ask others what the order they have received.