CryptoPortfolio - Simple trick to increase returns by 8% per year - Part 1: Geometric and Arithmetic Returns

Summary

Cryptocurrencies are extremely volatile. This creates an interesting opportunity to extract extra returns from rebalancing a portfolio and extract a “diversification dividend”.

In Part 2: Portfolio Risk and Diversification I quantify the effect.

In Part 3: how to make 8% more per year I calculate how much it can mean for the average portfolio

Geometric and arithmetic returns

First of all bit of definitions:

• Geometric returns are what you eat, it's the real compounded return that you can spend and hence it's what you want to achieve with any investment
• Arithmetic returns is an approximation of the above that is simpler and hence people tend to use it more often

Example: if you gain 10% then lose 10%, your arithmetic return is just the sum of the two which is zero but in reality you lost 1% (which is your geometric return). To see it take 100$, gain 10% and go to 110$ now the 10% loss will be 11$ so you end up with 99$.

The arithmetic approximation works relatively well with normal markets which move only a little, if you repeat the exercise above with gain and losses of 1% you get very close to zero.

But it works poorly with big moves: try with 50% gain and loss and you'll see that the portfolio is now down by 25%.

Cryptocurrencies are particularly volatile and hence this effect is particularly important.

As an aside, by the way, this means that for a crypto like bitcoin (which has a 40% to 80% volatility) to be a good investment you need some basic returns just to compensate for the Geometric effect. We will see how much later.

Geometric and arithmetic mathematical relationship

A well known formula links Geometric and Arithmetic averages and states

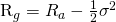
Where

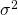• is the variance of the returns
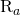• are the arithmetic returns
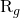• are the geometric returns

This means that with 40% volatility you need to have a 8% annualised return (40%^2*0.5=8%) just not to lose money on average.

Bitcoin so far had a much higher return so we are fine.