
I've been fairly busy lately, so I thought I would share with you guys a short essay I wrote a few years back on Georg Cantor. Cantor was a German-Russian mathematician who made significant contributions to set theory and showed that infinite numbers can differ in size, just as regular numbers. I hope you like it!
Georg Ferdinand Ludwig Philipp Cantor, the principal contributor to the development of set theory, was born in 1845, in St. Petersburg, as the son of a successful merchant. His father, Georg Waldemar Cantor loved culture and the arts, and his mother Maria Anna Böhm, a russian woman, was a talented musician, a trait which young Georg developed as well as he became a capable violinist in his own right. When Cantor was eleven, the family moved to Germany due to Cantor’s father’s poor health and altough he lived there for the whole of his life, he nevertheless retained a warm nostalgia for his place of birth [1].
In Germany he was educated at the Realschule in Darmstatdt, showing exeptional skills in mathematics, especially in trigonometry. Post-graduation he enrolled in the Polytechnique of Zurich in 1862, where he studied up until the unfortunate death of his father in 1863, after which he moved to the University of Berlin befriending notable mathematicians like Kronecker (who would later become a fierce critic), Weierstrass and Krummer. In 1867 he published his first work on number theory, the ‘De aequationibus secondi gradus indeterminatis’ (on indeterminate equations of the second degree), and was starting to experience the first of many depressive episode at the young age of twenty-two.
In 1869 he started working at the University of Hall, where he remained for the rest of his life, completing his most important works, while in active correspondence with many of his contemporary mathematicians. I will now briefly list his notable works from 1869 onward and then I will proceed to discuss in more detail some of the more intriguing points.
- In 1873 Cantor proved that the set of all rational numbers is countable, i.e, he showed that they may be placed into one-to-one correspondence with the natural numbers:
In mathematics a set is countable if and only if it is finite, or it is infinite and one can find a one-to-one correspondence between the elements of the set and the set of natural numbers. In order to show that there is this corrspondence one must assign a natural number in an infinite line to each element in the set of all real numbers like this [2]:
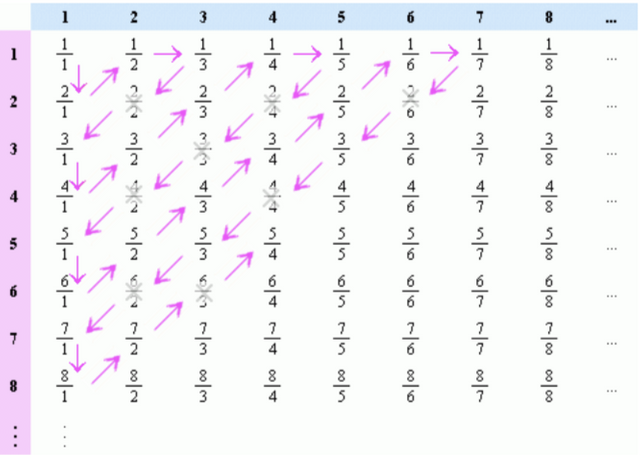
It should be visible that one can set all the elements in the set of all rational numbers into correspondence with natural numbers like this. It works in the exact same way with the negative integers.
- Between 1879 and 1884 Cantor published a series of six papers
in Mathematische Annalen designed to provide a basic introduction to set theory, the ideas of which were being received very badly and were ridiculed by his sometime friend Kronecker. The fifth paper in the series—The Grundlagen einer allgemeinen Mannigfaltigkeitslehre proved important, because Cantor was aware of the poor reception and designed the fifth paper to answer various criticisms. The major achievement in the paper, however has been claimed to be „its presentation of the transfinite numbers as an autonomous and systematic extension of the natural numbers“ [4].
This mathematical work led Cantor into general philosophical propositions about infinity :
„One goal of the Grundlagen was to demonstrate that there was no reason to accept the old objections to completed, actual infinities and that it was possible to answer mathematicians like Gauss, philosophers like Aristotle, and theologians like Thomas Aquinas in terms they would find impossible to reject. In the process Cantor was led to consider not only the epistemological questions which his new transfinite numbers raised but to formulate as well an accompanying metaphysics. Arguing the mathematical consistency of the new theory, and thereby asserting its legitimacy, was not enough. He felt compelled to defend his work from any form of attack, on whatever level, and therefore he was anxious to consider philosophical and theological objections that might be raised against the concept of actual infinities“. [3]
Cantor believed that a mistake in the history of philosophy and mathematics has been perpetuated since the time of Aristotle, who claimed ’infinitum Actu Non Datur’, that is that ’Actual infinity is an insconsistent notion’. By actual infinity he meant something which is completed and, at the same time consists of infinitely many elements. Potentially infinite, however, he saw as something to which more elements could always be added, but never infinitely many. A typical argument used to support this by the scholastics—the so- called „annihilation of number— went something like this:
If the (actual) infinite is admitted, then the finite numbers would be swallowed up by any infinite number or magnitude. For example, take any finite numbers a and b which are both greater than zero. Now, if their sum can be shown to be
a + b > a, a + b > b and if b was infinite, then no matter which finite value a might assume, a + ∞ = ∞ would result. Since this violated the way which numbers were usually understood to behave—the sum of two positive numbers ought not to result in the sum of one of them, they thought—they rejected infinite numbers as inconsistent. [4]
Cantor opposed this form of argument, because he thought it fallacious to assume that infinite numbers have to exhibit the same characteristics as finite numbers. Using his theory of transfinite ordinal numbers he demonstrated that infinite numbers were suspectible of modification by finite numbers:
It is improper to assume that infinite numbers should be constrained to follow principles established for finite numbers, says Cantor. Under the rules of transfinite arithmetic it is not that 1 + ∞ = ∞ and the ’1’ gets annihilated, but that in the case of ( ∞ ) + 1 = ( ∞ + 1) it does not. Under the rules of transfinite arithmetic it actually modified the number , which come in different sizes [4]
In philosophical terms, then, Cantor can be said to strongly favour the view that potential infinity is not actually a true form of infinity: all infinities are actual.
Thanks for reading!
Sources
- http://www-history.mcs.st-and.ac.uk/Biographies/Cantor.html
- I Grattan-Guinness, Towards a biography of Georg Cantor, Ann. of Sci. 27 (1971), 345-391.
- http://www.homeschoolmath.net/teaching/rational-numbers- countable.php
- J W Dauben, Georg Cantor: His Mathematics and Philosophy of the Infinite (Cambridge, Mass, 1979; reprinted 1990).

Nice article, it's always fascinating to see the boundries between mathematics and philosophy disappear.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Thanks friend, interesting channel you've got there
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
I just studied a panel 3 Golden Nuggets a day - on Infinity, I find it really interesting to understand what peers think of the geniuses in their ranks, Cantor's infinity study is certainly unique, I wish he renamed this infinities, but there is space for someone else to do it if following his study with today's tech.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Cantor's discoveries are highly interesting, I had a great teacher who blew my mind explaining them to me a few times. In any case, the existence of infinities of different sizes shows us the limitations of natural language expressions and common sense understanding.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Thanks for the follow @cryptoasis I am doing a survey. What posts would you like to read from my blog?
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Hey, I'd probably check out the bits on formatting.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Cloud Mining Bot:
t.me/Cloud_MiningBot?start=577299606
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
thanks for following!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
You're welcome!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Congratulations @cryptoasis! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on any badge to view your own Board of Honor on SteemitBoard.
To support your work, I also upvoted your post!
For more information about SteemitBoard, click here
If you no longer want to receive notifications, reply to this comment with the word
STOPDownvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
A great read this is @cryptoasis
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Thank you!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit