What is Cryptocurrency Game Theory: A Basic introduction - An in-depth guide by BlockGeeks ( A GREAT READ FOR ANY NEWBIE WANTING TO LEARN MORE)

What is Cryptocurrency Game Theory? One of the greatest innovations of the 21st century is, undoubtedly, the advent of cryptocurrency.
What is that makes the blockchain technology such a breakthrough? Let’s look at the real world and how fiat currency is maintained and stored. No matter who you are, your money is going to be stored in a centralized location, i.e. the bank. The problem with this model is that you are giving your money over to an entity and it is at the risk of getting compromised because of a variety of reasons. The blockchain solves this problem by being completely decentralized and corruption free internally. The way it achieves this is by the incorporation of cryptography and game theory.

What are market structures?

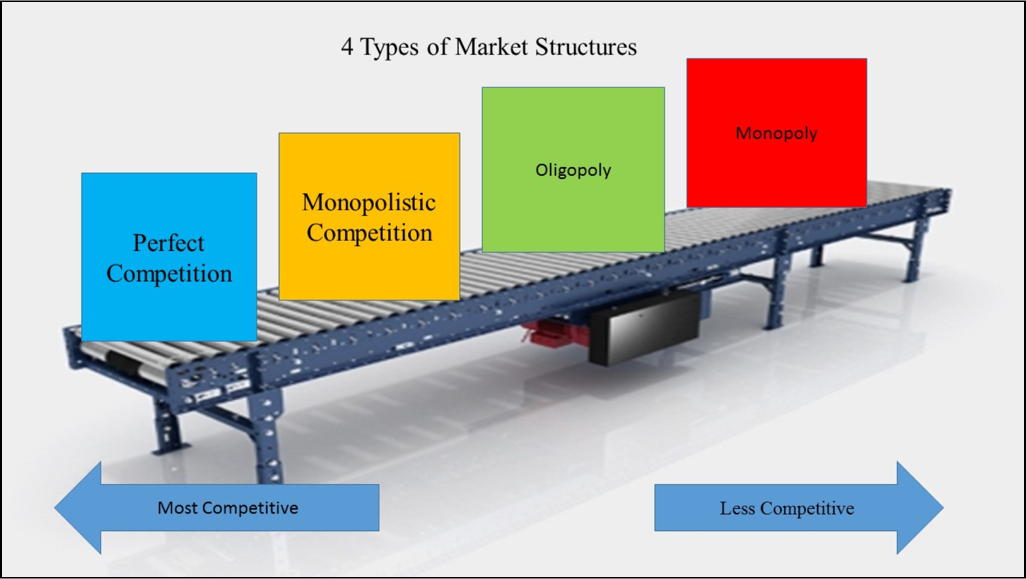
Before we understand the concept, we need to go through some basics first. The organization and fundamental characteristics of any market are called market structure. The market structures are differentiated based on many factors like a number of producers, control over prices and barriers to entry. Based on these factors, there are four different kinds of market structures:
Perfect Competition.
Monopoly.
Monopolistic Competition.
Oligopoly.

Perfect Competition

Perfect competition is a market place where it is easy for anyone to get into the market and individual sellers don’t have any power over the price of the product. Think of mangoes. It is easy for anyone to get into the market, all that anyone has to do is to grow mangoes. Plus, they can’t willingly change the price of the mangoes. If one person sells a mango for $10 then the buyer can simply buy it from someone who is selling mangoes for $5.

Monopoly

A monopoly is the polar opposite of a perfect competition. This is a market place which is dominated by one corporation and the barriers to entry are so high that nobody else can enter it. De beers diamonds are a great example of a monopolistic market.

Monopolistic Competition

This is a marketplace which has a lot of sellers and very low barriers. Their products are similar but not really identical. Think of the pizza delivery service. Now, dominoes and pizza hut have the same product with subtle differences. Obviously one can slightly price their product a little higher based on factors like customer preferences. However, if dominoes price their pizzas way too high, then people will simply go over to pizza hut. Consequently, if dominoes and pizza hut both start overcharging, since the barriers to entry is so low, another player can come in and take all the customers.

Oligopoly

Oligopolies are market places which are dominated by a few markets and the barriers to entry are high. One of the best examples of an oligopoly is the smartphone market. The market is dominated by few number of companies like Samsung, Apple, and Huawei. Much like monopolistic competitions, the products are similar but not identical. While this does give them some control over their prices, they don’t really have much of a leeway. If tomorrow, Apple decides to price their iPhones at $4000, apart from the Apple fanatics, most will simply opt for an Android phone. Obviously, they can always get together and decide as a group to mutually increase the prices, but this is called “collusion” and is illegal in many countries, including the United States.

So, when they can’t compete by changing prices, how can they get that edge over their competitors? They do so by “non-price competition”, which means competing without changing the price. How do they do that? They do so by changing the look and style of their products and giving a unique experience. However, the most recognizable form of non-price competition is advertising.

Advertising is one of the most effective ways of showing unique qualities of your products and to introduce new products. But then again, there is a problem. How many of the advertisements do you watch actually stick? Chances are that you have been bombarded by tons of ads today itself, how many of them do you actually remember? If you are a player in an oligopoly and you keep blindly advertising, you are going to be spending a lot of money.

As a result of that, in order to make up all that money, you are going to invariably have to increase the price of your products. If that happens, your buyers are simply going to go to your competitors. So how do you go about this? How do you advertise your products without losing out on your customers? You will have to basically take decisions based on the actions that your competitors will take. In order to do that, you will have to use Game Theory.

What is the Game theory?

Game theory is the study of strategic decision making. This is how many corporations make decisions while keeping in mind the actions that their competitors will take. Game theory was devised by John Van Neumann and Osker Morgenstern in 1944 and was considered a breakthrough in the study of oligopoly markets.

Since then the game theory has found a life of its own and has seen widespread implementations in various other technologies and fields.

A game theory model has at least 3 components:

Players: The decision makers. Eg. The managers in the firms.
Strategies: The decisions they want to take to further their companies.
Payoff: Outcome of the strategies.
In game theory, there are two types of games.

Zero sum game: It is a game in which the gain of one player comes at the expense of another player.
Non zero sum game: A game where the gain of one player doesn’t come at the expense of another player.

So, how does one apply game theory? Let’s go back to what we were discussing again, should or shouldn’t a company advertise a particular aspect of their product. Suppose there are two firms A and B.

The table that you see above is called a “payoff matrix”. The table basically reads like this:

If Firm A and B both decide to advertise then the payoff for both of them is 4 and three respectively.
If Firm A doesn’t advertise and B decides to advertise, then the payoff is 2 and 5.
If Firm A advertises and B doesn’t advertise then the payoff is 5 and 1.
If both Firms A and B don’t advertise then the payoff is 3 and 2.

So, what decision should both A and B take which will give them the best pay off? To solve this, we need to look at the scenario that serves both A and B.

Firstly, let’s look at Firm B.

Case 1: If Firm A advertises
Then Firm B has a payoff of 3 if they advertise and one they don’t advertise. So, obviously, their best payoff lies in advertising.

Case 2: If Firm A doesn’t advertise
Then Firm B has a payoff of 5 if they advertise and 2 if they don’t advertise. In this case their best payoff lies in advertising.

Conclusion: Regardless of what Firm A does, Firm B should advertise.

Now, let’s look at Firm A.

Case 1: If Firm B advertises
The Firm A has a payoff of 4 if they advertise and 2 if they don’t advertise. So, once again, their best payoff lies in advertising.

Case 2: If Firm B doesn’t advertise
In this case, Firm A has a payoff of 5 if they advertise and a payoff of 3 if they don’t advertise. Once again, their best payoff lies in advertising.

Conclusion: Regardless of what Firm B does, Firm A’s best strategy lies in advertising.

So, in this example, for both Firm A and Firm B, their most stable state will be if they both advertise, which is:

For both Firm A and Firm B, this is their dominant strategy. A dominant strategy is the best course of action for a player regardless of what the opponent does. In this example, (4,3) is also the Nash Equilibrium.

What is Nash Equilibrium?

The Nash equilibrium is a solution to a game where each player chooses their optimal strategy given the strategy was chosen by the other and they have nothing to gain by shifting their strategy. This was formulated by John F Nash who was portrayed by Russell Crowe in the movie, “A Beautiful Mind”. This has humongous implications in a distributed computer system like the blockchain. In fact, the blockchain is “cheat-free” because the entire protocol is in a Nash Equilibrium. We will discuss this later, but for now, let’s see the Nash Equilibrium in action in one of the most famous game theory concepts.

The Prisoner’s Dilemma

Ahh.. the good old prisoner’s dilemma. Chances are that if you have any idea about game theory then you must have come across this problem. Anyway, let’s get right to it. Suppose Rob and Ben were caught stealing a liquor shop and during the investigation, it was discovered that both of them have committed a far more serious crime in the past, say a bank robbery. During the investigation, the cops interrogate both of them and present them with a proposition.

Proposition 1: If you both don’t rat the other guy out then you will both get four years in jail.
Proposition 2: If one of you rats the other one out then the person who confessed will get 0 years while the other gets seven years.
Proposition 3: If both of you confess then you will both get two years each.

So, to put this is a pay off matrix:

Anything that is in RED is Ben’s and anything in BLUE is Rob’s.

So, now let’s analyze.

Obviously, Rob and Ben are hardened criminals and they won’t rat anyone out because there is “honor among thieves.” As romantic as that notion may sound, behavioral psychology and game theory tells us otherwise. Let’s look deep into it.

If they both confess, then the payoff matrix says that the outcome is (4,4). Meaning they both get 4 years each. However, that is a very unstable state because they both know that they have a better deal on the table. If they do rat the other person out, then they will have 0 years to serve. Because of this, this case is a very unstable scenario.

This is why, contrary to what pop culture tells us, in a situation like this, Nash Equilibrium happens when both of them rats the other one out. This is how Rob and Ben reach their optimal solution keeping the other’s strategy in mind.

But this brings us to a problem.

What if there is a scenario where the optimal solution for both the players lies in the scenario which has bad implication towards the society? Think of this scenario where Rob and Ben are planning a bank heist. Let’s make a matrix of positive payoffs that they will get in this scenario:

As you can see, in this hypothetical scenario, the best and most optimal strategy lies in both Rob and Ben stealing. While this might be good for both of them, it is not a good scenario for the society.

This is where the idea of “punishment” comes in.

What is Punishment?
The world is not necessarily a kind and fair place. Men are generally very corruptible and if not kept under check. In the real world, people will generally have a lot of opportunities to get corrupted without any consideration for the society in general. So the way we keep things like this in check is by implementing a punishment strategy.

So suppose in the example shown above we have a punishment strategy that goes like this:

“For every -0.5 of utility taken from the public a punishment factor of -7 will be given.”.

In other words, every act that is considered “bad” for the society will have their payoff deduced by 7 and that will cost -0.5 in utilities for the society. Now, you may be thinking why will society do anything like that? There is a loss of utility for the society which can be money, time anything and on the other hand, the people who are committing a crime are getting a terrible punishment as well.

But the truth of the matter is that we, as a society, have always integrated this in our daily life. What adding the punishment factor does is that it reduces the payoff from “bad” activities and changes the matrix like this:

See how the payoff from the “bad” activity for deduced by a factor of 7?

As you can see, by adding the punishment factor, the Nash Equilibrium changes from something that could have been bad for the society to something that is good for the society. So it changes from, Ben and Rob doing the bank heist to Ben and Rob doing the bank heist but also facing the consequences of a punishment.

So, going back to the question, what is the incentive for a society to go through the punishment? Why will they want to waste their utilities? The way that people have answered this question is by making punishment mandatory. In, other words, if someone is a society doesn’t go along with the punishment, then they themselves become criminals and are subject to punishment.

How does that apply in a civilized society? Think of a police force that is funded by tax taken from the people. In this case, we have a specialized force which will dole out the punishment and the way the society takes part in it is by paying their taxes which fund the force. If you do not pay the taxes, then you are subject to punishment as well.

Another interesting example of “punishing the non-punishable” is social ostracization. Think of a society where a person, says Max, has committed a crime. Instantly he becomes an outcast in the society. This is a scenario where everyone in that society is participating in the punishment. Now suppose, someone does mingle with Max, that person also, by association, will become “bad” and he/she, in turn, will be ostracized by the society as well.

It wouldn’t be a stretch to say that this very concept is the reason why we aren’t all dead right now.

The concept of Nash Equilibrium and Punishment has heavy implications in blockchain and keeping the miners honest. We will explore that in a bit. But before doing so, we must go through some more basic game theory models.

The Schelling (Focal) Point

The great economist Thomas Schelling conducted an experiment with a group of students asking them a simple question: “Tomorrow you have to meet a stranger in NYC. Where and when do you meet them?” He found out that the most common answer was, “Noon at the Grand Central Terminus.” This happened because the Grand Central Terminus, for New Yorkers is a natural focal point, the focal point is also known as a “Schelling point”.

So, to define a Schelling point: It is a solution that people will tend to use in the absence of communication because it feels special, relevant or natural to them.

Let’s demonstrate this concept with a game. Suppose there are two prisoners kept in two different rooms and they are given a random series of numbers. Then they are told to guess the number that they another prisoner will guess, without any communication between the two. If they guess the wrong number, then they will be killed (just to up the ante).

The numbers that they are given are:

7816239, 676716313, 100000000 and 871823719.
Which number do you think they will choose?

Why? Because it is different and special when compared with the rest of the numbers and that is why it is Schelling point. Throughout our history, human beings have unknowingly sub consciously converged in various places such as bars, churches, community centers, etc. because in a society those places are common Schelling points.

A very famous example of the Schelling point in action is a game that we hope you have never played in your life called “The Chicken Game.” This is how it works, two people ride towards each other on a bike. If they collide head on, they die. However, the first person who swerves away from the incoming rider is a “chicken”.

So, in this game, there are two scenarios which can end in a crash:

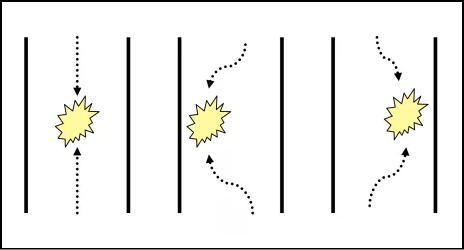
Case 1: Both riders head towards one another.
Case 2: One rider swerves left and the other swerves right.

Thomas Schelling gave the solution to this using the concept of focal points. He said, that the best solution to this game is to not look at the other rider in the eye (i.e. cut off communication with the other rider) but focus on one’s own instincts. Since, in the United States, people drive on the right side of the road, if we let our instincts take over, we will automatically steer the bike towards the right side, because that’s where our Schelling point lies.

Grim Trigger Equilibrium

In order to understand how a grim trigger equilibrium works we need to think of a scenario. Let’s imagine a social situation where monarchy still exists and it is believed that kings get to rule over others because of a divine right from the Gods. However, in a society like this, if the king is killed then automatically the law of divine right disappears because it will be apparent to everyone that the king is not a divine being. What this will do is that it will open all the floodgates.

Now that it is apparent to everyone that the king is killable, it will start an endless cycle of bloody revolutions where nothing can stop from all the subsequent future kings from getting murdered. The only way to stop this vicious cycle is by NOT killing the king in the first place and to maintain the notion of “divine right”. This is called a Grim Trigger Equilibrium. Think of it as a state wherein if you deviate even a little bit you are going to cause an endless cycle of recursive punishment.

Coordination Problems

Consider this matrix:

Now, if you see this matrix, there are two Nash Equilibria: (A, A) and (B, B), deviation from either of the state won’t benefit them. The idea of this game is how can you convince people to go from (A, A) to (B, B)? If there are a small group of people involved then that is relatively simple, you can simply coordinate via phone or emails. But, this changes when we are talking about a huge group of people.

The fundamental difference between prisoner’s dilemma and coordination problem is that in prisoner’s dilemma, both the players had to choose (B, B) because that was the choice that had the most payoff even though (A, A) is a morally better solution. In Co-ordination problem, it is not about the morality or the payoff, it is the incentive for a person to go from one state to another. Why should a huge group of people change the way they do things?

A coordination game fails when an only minority of the group change their state, and the majority don’t, and inversely, it is a success when a majority of the group changes their state. Let’s see that with an example.

Suppose we want to change the language to a symbol based language. Eg:

Original statement: “Give me your number?”
New statement: “#?”

If only you speak using this language, it will be a failure because the majority won’t understand what you are talking about and you will be shunned from conversations aka the payoff for you is very low, and you have no incentive to change.

However, if the majority of your society shifts to this language and use it exclusively, you will have to change your language otherwise you will never be able to fit in. Now the incentive for you to join is high.

Why do you think nobody speaks in ye olde English anymore? If you talk like that in your society, you will be shunned, and everyone will think “thou art a knave sirrah!”

The concept of Bounded Rationality

Imagine this scenario, Sarah goes to the grocer’s shop every single day and buys an apple. She does this every single day as a ritual. However, every day she faces a situation. Every day, whenever she is in the shop, the shopkeeper leaves for 5 mins and there are no security cameras in place. She can easily shoplift an apple and nobody will get to know about it. Yet she never does that.

What Sarah does here is called “Bounded Rationality”. Bounded rationality basically means that when given a choice, people will always follow a path that is simple and something they are used to. This path may not be what is best suited for them and it may not give them the highest pay offs, yet they will always follow the simplest path. The reason why Sarah chose the virtuous path of following her simple routine everyday instead of shoplifting and getting away with no repercussions is that the second scenario is a little more complex than her simple everyday routine.

Now that we have gone through some game theory models, let’s see its implication in cryptocurrency and how it helps keep the system floating.

Blockchain and Cryptocurrency Game Theory

A block is a series of blocks which contains individual transactions in it. Each block also contains the hash of the previous block and this, in turn, links each subsequent block to the previous block making a chain. Hence the term, “blockchain.” This is a rough visual representation of a blockchain.

Some terms:

Genesis block: The first block of the blockchain is called a “genesis” block.
Proof of work: The amount of computational work required to create the block.
Parent block: The block that immediately precedes a block is the parent block of that block. So in the diagram above, Block 50 is the parent block of Block 51.

Every block in the blockchain has a scoring function.

Score(genesis) = 0.
Score(Block) = Score (parent block) + Proof of work
The current state of the chain is the block with the highest score.

In a system based on blockchain Bitcoinitcoin there are two players:

Users.
Miners.
Users, in bitcoin, have only two functions available to them:

Send coins.
Receive coins.

In order to do that they need two keys, the public, and the private key. What miners do is that they authenticate the transactions AND they do the process of mining. Mining is how new blocks are discovered and added to the blockchain.

Block Mining
Through a series of computations, miners find a block and add it to the blockchain.In Ethereum, adding the block gives the miner(s) a reward of 5 ether and In bitcoin, the mining reward is 25 BTC (both as of writing). Miners have a lot of power in the blockchain system and if they do choose to cheat for their own personal gain, they can cause havoc in the system.

To mitigate that, the blockchain uses game theory mechanics to keep the system bulletproof. In order to understand how game theory keeps the miners honest, let’s take a look at another peer-to-peer system which has allowed its users to, time and again, get away with cheating.

Torrenting is one most popular peer to peer systems in the world. While using torrents, users have two roles: downloading and seeding. After downloading a file, they are supposed to share it the network via a method called seeding. However, they get no compensation for seeding the said file and hence more often than not they refuse to do so. Most torrent users are “cheats” because they do not seed their files. They can get away with cheating because the system doesn’t have a “punishment model” the way blockchain does.

How can miners cheat?
They can include an invalid transaction and give themselves extra coins.
Add blocks randomly without worrying about Proof of work.
Mine on top of invalid blocks to get more BTC.
Mine on top of a sub-optimally scoring block.

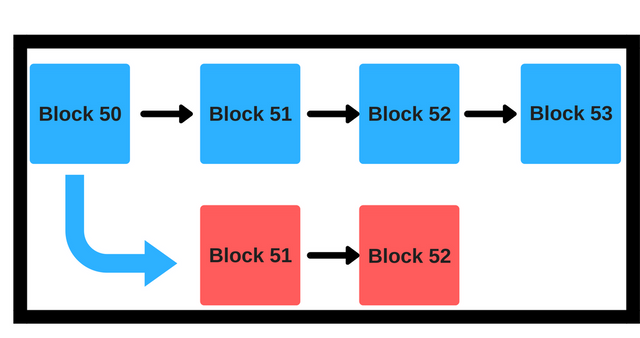
The blocks in blue are the main chain. Now suppose there is a miner who, in blue block 51, spends 20 bitcoins to get 500 litecoins (hypothetically). And now he wants to create a parallel chain with a new block 51 (red), where in he never did this transaction. So, to simplify what he just did, let’s do a quick recap:

In blue block 51 spends 20 bitcoins to get 500 litecoins.
Creates a new chain (fork) from block 50 and in the alternate block 51, he doesn’t do the litecoin transaction.
In the end, he comes out with his original 20 BTC and 500 new litecoins.

What just happened here is called “double spending.” Obviously now miners can, theoretically, mine on top of the new red chain and keep double spending and mining extra bitcoins. As you can imagine, this can destroy the bitcoin system.

So why don’t miners do that? Is it because they are all good and honorable people? You can’t make a system based on the morals of a person, morality is not quantifiable after all. This is where the true genius of blockchain comes in. The blockchain was designed in a way that it is a self-enforcing Nash Equilibrium. The reason why that happens is that mining has a recursive punishment system.

The Nash Equilibrium in mining and the punishment system.

If a miner creates an invalid block then others won’t mine on top of it because of a rule that has been defined in blockchain mechanics. Any block that is mined on top of an invalid block becomes an invalid block. Using this rule, miners will simply ignore the invalid block and keep on mining on top of the main chain aka the blue chain in the diagram.

This similar logic stands for sub-optimally scoring block. Look at the diagram again. No miner will want to mine on Red Block 52 because the Blue Block 53 will have a higher score than the red block.

Both of these scenarios get mitigated because miners., as a group will choose the most stable state aka the state with a Nash Equilibrium. Obviously, you can make all the miners mine on the red block and make it the new blockchain, however, the number of miners is so vast that an event like that simply cannot be coordinated (we will talk about this in a bit). As the co-ordination game states, if a majority of the people in the group are not changing their state, the minority will not have any incentive to stay in the new state. Seeing this, why will a miner spend all their computation power and risk ostracization in a futile cause?

Why will users use the main chain instead of the other chain?

So, now that we have seen the reason WHY miners will prefer the blue chain…What about the users? In the blockchain game, there are two players, miners, and users. Why will users prefer the blue chain over the red chain? Once again, game theory mechanics come into play.

The first thing that you need to keep in mind is that cryptocurrency has value is because the people give it value. So, why will a normal user assign a value to coins coming out of the blue chain and not to the coins coming out of the red chain? The reason is simple. The main chain is a Schelling point from the users perspective. They give it value because the main chain seems natural and special to them.

Bounded Rationality: Another reason why users will value the main chain more is that they are simply used to it. Like bounded rationality states, people will simply opt for the simplest solution every time. Moving through a newer chain needlessly complicates things.

What is the Proof Of Work Takeover Problem?

Before we start explaining this, let’s bring back our old diagram again for reference:

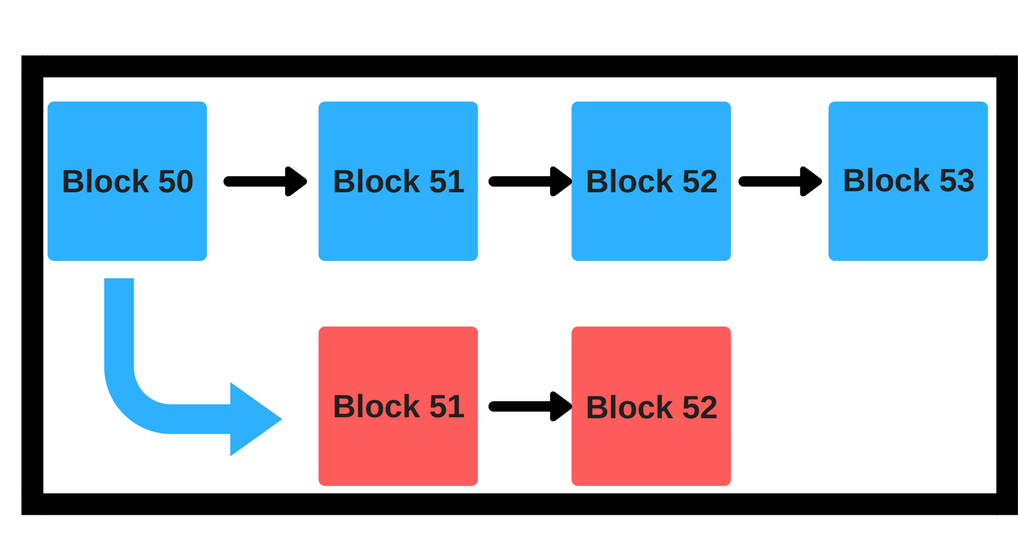
Vitalik Buterin gave a great example of the Takeover problem and we are going to expand on it. Suppose, someone makes a hypothetical smart contract for an activity. The terms of the contract go like this:

Any miner can join the activity by sending a very large deposit into the contract.
The miners must send shares of the partially completed blocks that they have mined into the contract and the contract verifies it and also verifies that you are a miner and that you have sufficient hash power.
Before 60% of the miners in the system join you can leave anytime you want.
After 60% of the miners join, you will be bound to the contract until the 20 blocks have been added to the hard fork chain aka the red chain.

Yes, it is indeed very diabolical and you can see the problem that this attack can have. Not only will the new chain grow bigger and longer, since 60% of the entire miners are bound contractually to this new chain this will quickly make the original older chain aka the blue chain irrelevant. This will make double spends all over the place and the value of the currency will fall fast.

Now, you might be asking why miners will join in a takeover?

Well, let’s see their incentive for joining:

The possible reward at the end.
No risk of joining on their part.
What is their incentive to follow through with the contract?

The huge amount they have deposited in the beginning.
Once again, the possibility of a great reward.

Theoretically, a takeover like this can end any currency, but this is not that likely to happen because of…You guessed it…. game theory mechanics.

Grim Trigger argument to the rescue!

Think of our king argument when we first talked about grim triggers. If a king is killed and usurped, what will stop the new king from getting killed and from this becoming an endless bloody cycle? To stop this from happening, the best course of action is to not kill the original king in the first place.

Similarly, let’s use this logic for blockchains. If a blockchain is taken over and destroyed and the miners are diverted into a new chain, what is stopping that new chain from being taken over by the majority anytime soon? To stop these endless hardforks (aka the red chains in the diagram) from happening, it is important that we don’t do the takeover in the first place.

However, there are certain places where the Grim Trigger argument does fail, and obviously, there are places where it works pretty spectacularly:

The argument fails when the miners are not bound to singular currency. If the miners are working on several currencies, then they can simply group to take over a low-value currency.

The argument holds up if they are bound and loyal to a particular currency. After all, it is in their direct interest to uphold and maintain the value and legitimacy of the currency.

If the currency requires specialized ASICs, then the grim trigger argument holds up. If a currency can only be mined by specialized software, then miners will make sure that nothing happens to that particular currency and that it doesn’t lose value. Specialized ASICs after all, can only work for a particular currency. Otherwise, it is useless. Plus, they are expensive.

The argument doesn’t hold up if the currency can be mined using CPUs. CPUs are not expensive after all, and it can be used to mine other currencies.

However, if the miners who own the CPUs have a stake in the currency, the argument holds up because they don’t want to lose the stake that they have invested in the currency. This is a sort of proof-of-stake.

Conclusion

As can be seen, game theory mechanics are what make blockchains so special. Nothing about the technology or mechanics is new, but it is the marriage of these two fascinating concepts that has made cryptocurrency secure from internal corruption. Even if bitcoin and Ethereum do fail for whatever reason, cryptocurrency will always live on because of this path breaking a partnership.