Blockchain y la teoría de juegos, parte II

En la primera parte de Blockchain y la teoría de juegos, hablamos de las estructuras de mercado e hicimos una breve introducción a la teoría de juegos. A continuación, conversaremos sobre la teoría de juegos con más detalle, y sobre el equilibrio de Cournot y Nash, también llamado "equilibrio del miedo".

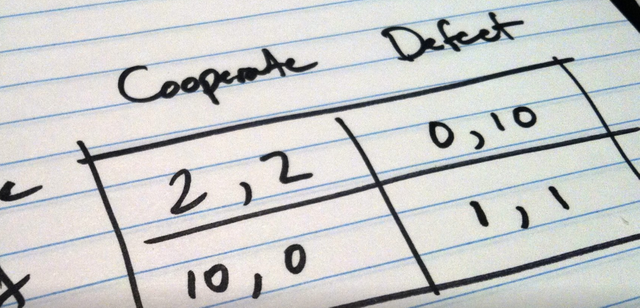
Imagen: Medium.com

¿Qué es la teoría de juegos?

La teoría de juegos es el estudio de la toma de decisiones estratégicas. Así es como muchas corporaciones toman decisiones teniendo en cuenta las acciones que tomarán sus competidores. La teoría de juegos fue ideada por John van Neumann y Oskar Morgenstern en 1944. Desde aquel entonces, la teoría de juegos ha encontrado ha visto implementaciones generalizadas en varias otras tecnologías y campos.

Un modelo de teoría de juegos tiene al menos 3 componentes:

• Jugadores: los que toman las decisiones. Por ejemplo, los gerentes en las empresas.
• Estrategias: las decisiones que quieren tomar para promover sus empresas.
• Resultado: resultado de las estrategias.

En la teoría de juegos, hay dos tipos de juegos:

1. Juego de suma cero: es un juego en el que la ganancia de un jugador se obtiene a expensas de otro jugador.
2. Juego sin suma cero: es un juego donde la ganancia de un jugador no se obtiene a expensas de otro jugador.

¿Cómo se aplica la teoría de juegos a la toma de decisiones?

Supongamos que debemos decidir si la compañía para la que trabajamos debe o no hacer una campaña publicitaria para uno de sus productos.

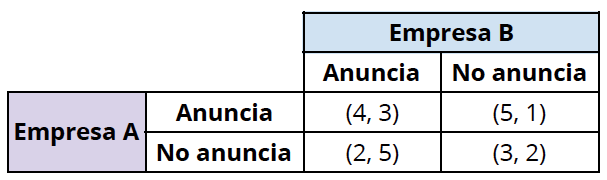
Imagen: @criptoEstratega

La tabla que se ve arriba se llama "matriz de pagos". En pocas palabras, expresa lo siguiente:

• Si las empresas A y B deciden anunciar, entonces la recompensa es 4 y 3, respectivamente.
• Si la empresa A no anuncia y B decide publicitar, entonces la recompensa es 2 y 5, respectivamente.
• Si la empresa A anuncia y B no anuncia, entonces la recompensa es 5 y 1, respectivamente.
• Si ambas empresas A y B no anuncian, entonces el pago es 3 y 2, respectivamente.

En vista de lo expuesto, ¿qué decisión deberían tomar A y B con el fin de obtener una mejor recompensa? Para resolver esto, es necesario mirar los escenarios que se presentan.

Imagen: @criptoEstratega

Entonces, en este ejemplo, la condición más estable tanto para la empresa A como para la B es si ambas hacen campañas publicitarias para sus productos. Para ambas empresas esta es la estrategia dominante.

Una estrategia dominante es el mejor camino que un jugador puede seguir independientemente de lo que haga su oponente.

El ejemplo precedente (4, 3), también representa lo que se denomina “equilibrio de Cournot y Nash”.

Imagen: Huffingtonpost.com

¿Qué es equilibrio de Cournot y Nash?

El equilibrio de Cournot y Nash –también llamado equilibrio del miedo– es una solución para juegos con dos o más jugadores, el cual asume que cada jugador conoce y ha adoptado su mejor estrategia; y, que todos conocen las estrategias de los otros jugadores. Por tanto, cada jugador no gana nada modificando su estrategia si los otros no han cambiado las suyas. Así, cada jugador está ejecutando el mejor "movimiento" posible teniendo en cuenta los movimientos de los demás jugadores. Este concepto fue formulado inicialmente por Antoine Augustin Cournot en 1838, y completado en 1951 por John Forbes Nash. Este concepto tiene enormes implicaciones en un sistema informático distribuido como la cadena de bloques. De hecho, el blockchain está "libre de trampas" porque todo el protocolo está en equilibrio de Cournot y Nash.

El dilema de los prisioneros

Supongamos que Rafael y Ricardo fueron sorprendidos robando una tienda de víveres, durante el curso de la investigación se descubrió que ambos cometieron un delito mucho más grave en el pasado, digamos el robo de fondos públicos. Durante la investigación, la fiscalía los interroga a ambos y les presenta una propuesta conformada por tres opciones:

• Opción 1: si los dos no se delatan entre sí, ambos recibirán una pena de cuatro años en la cárcel.
• Opción 2: si uno de los ladrones delata al otro, el confesor obtendrá una peña de cero años, mientras que el otro recibirá una pena de siete años.
• Opción 3: si ambos ladrones confiesan su delito, los dos recibirán un castigo de dos años en la cárcel.

Imagen: @criptoEstratega

Ahora, analicemos el caso.

Es obvio que tanto Rafael como Ricardo son criminales consumados, y que no se van a delatar entre sí porque se profesan lealtad. Sin embargo, la psicología del comportamiento y la teoría de juegos nos dicen lo contrario.

Si ninguno de los dos confiesa, entonces la matriz de pagos dice que el resultado es (4,4), esto quiere decir que cada uno obtiene cuatro años de prisión. Sin embargo, este es un estado muy inestable porque ambos saben que tienen un mejor trato sobre la mesa: si delatan a la otra persona, tendrán cero años de encierro. En conclusión, la ocurrencia de este escenario es muy improbable. Entonces, en una situación como esta, el equilibrio del miedo sucede cuando ambos se delatan entre sí –teniendo en mente la estrategia del otro–. En este caso, cada uno debe cumplir con dos años de prisión.

Lamentablemente, esta situación no es tan simple, ¿qué pasa si hay un escenario en que la situación es favorable para los dos partes, pero desfavorables para la sociedad? Ahora pensemos que Rafael y Ricardo están planificando el robo a un banco. A continuación miremos la matriz de pagos positivos que se genera.

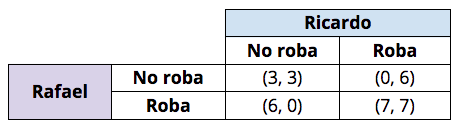
Imagen: @criptoEstratega

Como se puede ver, la mejor y más óptima estrategia radica en que tanto Rafael como Ricardo roben el banco. Si bien esto podría ser bueno para ambos, de ninguna manera es bueno para la sociedad. Aquí es donde entra la idea del "castigo".

Te invito a continuar con la tercera parte de este ensayo donde hablaremos sobre el castigo, el punto focal de Schelling, el equilibrio del detonante siniestro y los problemas de coordinación.

Por Juan Francisco Bolaños
@criptoEstratega

Tus donaciones voluntarias son muy bien recibidas, significan un gran incentivo para continuar con mi trabajo:

BTC: 19wyKAFfbJMBfizFyQCxCYEdYUDWeAPYo1
ETH: 0xe0722b3DE8Da45294477b7DC08BD7a078F7850dC
DASH: XbDcvPZf7ZUGbYKLLrS19whaehoMSFiN3M
LTC: LPi2EH4jhs6Aj7P74xPXYNnCvQNMGkUQQZ

Si te pareció interesante esta publicación por favor dale un voto y un "resteem". ¡Gracias de antemano!