Understanding a Raw Bitcoin Transaction

I wrote some code that outlines how to create a transaction from scratch. First I want to explain the concepts I found difficult to grasp, and the information that took me a while to find. Then I will walk through my code. I tried to keep it concise so I don’t bore you with the obvious or bombard you with lengthy explanations. This is the stuff I found interesting while learning about transactions. It is intended to be used in conjunction with other resources.

Elliptic Curve Cryptography

Bitcoin uses Secp256k1 for its elliptic curve digital signature algorithm. Secp256k1 has a prime order N = FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE BAAEDCE6 AF48A03B BFD25E8C D0364141, which is equal to the total number of points on the curve minus the infinity point. The infinity point is where X = 0. These points(not including the infinity point) make a cyclic group. Every cyclic group is an abelian group, meaning it has 5 rules that it follows. They are closure, associativity, identity element, inverse element, commutativity. We can use modulus to restrict the elliptic curve to manageable numbers while keeping all the important properties.

Addition

These properties allow us to define addition as 3 points a line intersects equals the infinity point. P + Q + R = 0. This also means two points equals another one, by moving R to the other side of the equation. The inverse properties tells us that -R equals R flipped over the X-axis. We can now find every point in the group, it would just take N additions. Starting from the base/generator point we can add it with the previous point to find the next one.

generator point(P) + 0 = P
P + P = - R
P + -R = new point(Q)
P + Q = another new point(public key)

None of the points will be the same, they will all be whole number coordinates and after N additions we will be finding the same points in the same order(hence cyclic). Each of these points is a public key. The private key is equal to the number of additions it took to reach the public key.

Doubling

The first line in the code above adds the generator point to itself, also called doubling. If a line is tangent to a point on the curve it will only intersect at two points. Doing N additions would make finding a private and public key pair a brute force task. We won’t know every key pair “Until computers are build from something other than matter and occupy something other than space.” We know how many points there are because of Schoof’s algorithm. Doubling allows us to easily calculate key pairs of large numbers. When the public key point is doubled so is the private key.

Modular Inverse

We need to use modular Inverse to calculate slope because division does not work with modulus. The Euclidean algorithm find the greatest common divisor(GCD) of two integers. The GCD of P( FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE FFFFFC2F) and any number less than it will be one because P is prime. Reversing the steps of the Euclidean algorithm(Extended Euclidean algorithm) gives us Bezout’s identity. This also gives us the modular inverse we need to calculate slope. The slope is used in addition and doubling. The slope at each point is still calculable over a finite field.

Discrete Log

The security of Bitcoin depends on discrete log and hash functions. It is hard to find a private key given a public key because there is no efficient way to solve the discrete log problem. The discrete logarithm log(B)A is an integer k such that B^K = A. This looks like elliptic curve multiplication. The generator point is B, it’s what we multiply the private key by to get the public key. The private key is K, it is the number that is hard to solve for. The public key is A, the result of the generator point multiplied by the secret/private key. Basically there are no known methods better than a brute force attack. Elliptic curves also provide more security per bit than RSA.

Code

Here it is. To generate a key pair we first need a private key. You can either use a random number or wallet import format. ECmultiply finds the public key using the most significant bit first. We need the binary form of the private key to know exactly how to add and double. The ECmultiply algorithm(double and add)is similar to square and multiply. The counter helps illustrate how the private key doubles and adds with the public key. The ECmultiply loop starts at one because the first bit is always a 1. This implied addition counts as one addition to the private key. The generator point is the public key when the private key is one. This code does not allow addition of the same point.

Public Key Generation

Step 1 generates the compressed and uncompressed public key. Any point in the cyclic group has only one other point with the same X value. The Y coordinates are also the same except one is flipped over the X-axis. No information is lost when reducing the Y coordinate to only a positive or negative value.

Decoding hex means going from hex to ascii. Encoding hex means going to ascii to hex. At step 2 before we can start hashing we have to convert hex to ascii. Hashing has to be done on ascii characters to work with this code.

Step 3 is called the public key hash, it is where coins are sent to in a raw TX.

Step 9 is smaller and more readable, but easily reverted to step 3. The address is a checksum and encoding of step 3. You can’t go backwards from step 3 to 1 because hashes are a one way function.

Bitcoin, Litecoin, and Vertcoin work the same for this kind of TX except for step 4. I used Vertcoin because it is cheap.

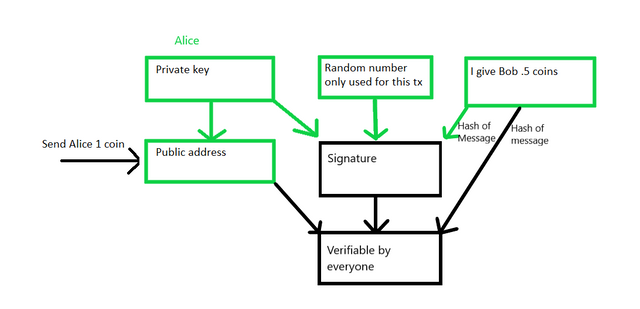
Here you can see all the components that make up a signing message and transaction.

Signing Message

We reference the transaction ID, the output from that transaction we want to redeem(input), and the public key hash we want to send to(output). We sign the hash of the message with a random number(1 to N), and the private key. If someone knows the random number you used they can calculate your private key. The signature proves you possess the private key to the address coins were sent to(input) without revealing the private key. This is verified by putting together your public key, the signature, and the message. We only use our private key to sign transactions, and produce public keys.

Little endian means bytes are ordered from smallest to largest. Byte 3f2e1d would become 1d2e3f. Big endian means it would stay the same.

Input scriptpubkey is where someone would have sent coins to if I gave them the public address from my private key. They can calculate it from my address, I can calculate it from my address or private key.

Transaction lock time is the earliest time that miners can include the transaction in the blockchain.

Sequence number can be used if your transaction is not final and you plan on updating it. This is not commonly used. If it is at its maximum value the transaction is considered final even if block time is not reached.

The signature produces an R and S value. These two values along with the public key, and the hash of the signing message verify the signature is authentic. This is where the step 1 public key is revealed.

Final Transaction

The final transaction is the same as our signing message except in our signing message is previous scriptpubkey. In our final TX this is replaced with scriptsig. Scriptsig confirms we know the private key to our public address. If any of the data in the TX changed the signature would not be valid because the hash would be different.

Transmitting

I used Ubuntu in VirtualBox and then installed the Vertcoin daemon. I used this to view raw transactions, and broadcast them.

I hope you learned something. I would appreciate any feedback, this is my first attempt publishing something.