After months of ventring into the world of modular arithmetic. On a mission to find a way to prime factorize large numbers. For the sake of its impact on some areas of cryptography, and hopeful impact on 'data compression techniques' and other particular topics out there. I also included a search for any mathematical method of forming a new cryptography algorithms as well while I'm at it. And before I knew it I was on to a lead. I dropped it for a while thinking it show little proof of progressive. Then some months later upon revisiting it, I unfolded a hiden mathematical mechanism suited for the very goal it was hope to be. Success! Lo and behold before my eyes a new public-key algorithm. Hence the illustration at [fig. 1] below.
fig. 1
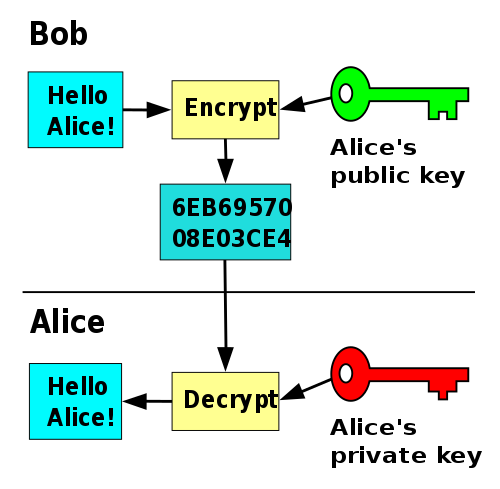
There is a well-known algorithm namely, the RSA algorithm in which one of the steps to the process of the technique involves further calculations to find for a random selected value, its 'modular inverse' value modulo the 'Phi' value output of 'modulo "N"'. For example:
P1=23, P2=19,P1*P2= [modulo N(mod N)]= 437, phi of [mod N]=396, [random private key(PrK)]=17, [mod inverse of PrK]=[public-key (PuK)]=233.
[PuK] is harder and harder each time to calculate for larger and larger numbers. Likely it could be exponentially larger each tim of trial per number growth, for all I can guess atleast.
What this new algorithm I have. It has the advantage over RSA is that the same step in the procedure of making private&public key pairs. It omits these for mentioned difficulties. Meaning that, one administrator while making his/her random private key then find the public with too little effort (aka a overly simple polynomial time calculation, even easy for a human). Without presenting threat to the security purpose of the algorithm.
Another new algorithm I have too, is one that can perform secret ket exchange over unsecured communication channels. It serves the same purpose as the Diffie Hellman key exchange algorithm. But with the advantage of not needing further dificult calculations such: " finding a list of primitive roots of modular from which to select". With this new algorithm I have, one only needs to concer him/herself with picking random values all the way. The easiness ofmaking arbitrary choices, still with the same level of security compared to defeat Hellman key exchange.
If I may I would like to invite conversations with any fellow Steemians who share an appreciation of cryptography algorithms and may also contribute towards the dream of getting this algorithm out there fully participating in the industry. And If hope would have it so, should it ever be the case it's proven and certified as competent as (if not more)any of the otherslready out there. May it find its place in some form of cryptocurrency scheme/s; existing or new. Thank to listeners for your attention. Also too your prospective support and/or well-wishing intent towards the endevor.
Congratulations @becomethreality! You received a personal award!
You can view your badges on your Steem Board and compare to others on the Steem Ranking
Vote for @Steemitboard as a witness to get one more award and increased upvotes!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit