
TL:DR Während Kevin sein Geld verzockt, hab ich Rosi die Funktionsweise von Wallets erklärt. Da ist ein private key aufgetaucht, den man sicher speichern muss. Bei der Verwendung von Wallet-Software hantiert man wiederum mit sogenannten Adressen, an die Bitcoins transferiert werden. Heute zeige ich Schritt für Schritt wie man von einem private key zur Adresse kommt und was das alles bedeutet.

Lass doch mal bitte diesen Scheiß mit Kevin und Rosi. Nimmt deinen Artikeln die ganze Ernsthaftigkeit.
Ich versuche halt das Thema aufzulockern. Das ist ganz schön trocken Brot sonst.
Man kann auch ernsthaft schreiben, ohne dass es trocken ist.
Wer bist du überhaupt?
Nenn mich Dirk. Ich will wissen, wie das wirklich funktioniert bei Bitcoin. Umgang mit der Konsole darfst du bei mir voraussetzen.
OK, Dirk. Ich hoffe, wir werden die Konsole nicht brauchen. Aber warum eigentlich nicht. Wer möchte, kann ein paar Schritte in der Konsole nachvollziehen, mit IPython und pybitcointools.
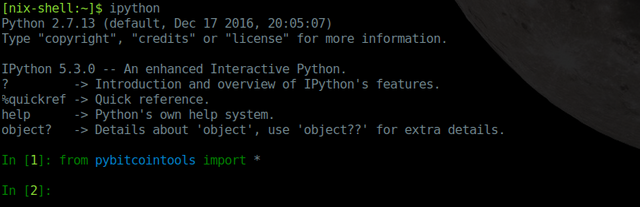
Da mag wohl jemand keine Windows-Nutzer. Was kommt als nächstes?
Dirk, sag eine Zahl zwischen 1 und 15792089237316195423570985008687907852837564279074904382605163141518161494336.
Fünf
Also wir brauchen vereinfacht gesagt eine 77-stellige Dezimalzahl. Das ist übrigens eine 256-stellige Binärzahl und belegt also 256 / 8 = 32 Bytes im Speicher. Aber fünf ist schon in Ordnung. Diese Zahl ist ab sofort unser Geheimschlüssel, engl. private key.

Wörter wie private key bitte nicht einfach ohne Erklärung verwenden!
Sicher es handelt sich dabei um einen Begriff aus der ...
... Asymmetrischen Verschlüsselung
Bei weiterem Interesse hilft Wikipedia. lch erkläre hier nur die Aspekte, die für Bitcoin wichtig sind. Bitcoin benutzt ein Verfahren namens ECDSA. Wir werden mit dem private key allerdings nichts verschlüsseln, sondern nur Dinge signieren. Aber ich greife vorweg. Zuerst erzeugen wir uns aus dem privaten Schlüssel einen öffentlichen Schlüssel, engl. public key.
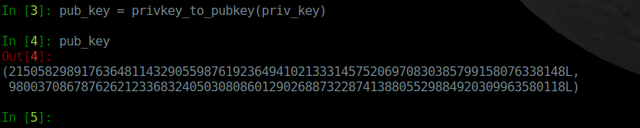
Wer genau hinschaut, sieht, dass das zwei Zahlen sind, und zwar eine x- und eine Y-Koordinate auf einer elliptischen Kurve. Die hat uns der ECDSA-Algorithmus ausgespuckt. Wichtig für uns ist aber nur: zu jedem private key existiert genau ein public key und dieses Schlüsselpaar hat zwei Eigenschaften: Die "Falltür" und das Signieren.
Falltür, klingt ja sehr technisch
Damit ist gemeint, dass man zwar aus einem private key einen public key erzeugen kann, aber nicht umgekehrt. Das ist sehr wichtig, denn den private key halte ich geheim, während ich den public key öffentlich machen will. "Falltür" heißt: Ich kann nur in eine Richtung und niemand erfährt je meinen private key.
Schon falsch: ich kann einfach für alle Zahlen von 1 bis 1077 den öffentlichen Schlüssel berechnen und dann kann ich den privaten Schlüssel nachschlagen
Das nennt sich Brute-Force-Attacke und du darfst die Größe der Zahl 1077 nicht unterschätzen. Wenn du eine Methode angeben kannst, um aus einem public key einen private key zu berechnen, die nicht so lange dauert, wie unserer Sonne alt ist, dann hast du ECDSA geknackt. Das hat noch niemand geschafft und deshalb gilt ECDSA (mit den richtigen Parametern) zur Zeit als sicher. Mit immer besseren Computern wird möglicherweise eine Anpassung der Parameter notwendig, oder sogar ein ganz anderer Algorithmus.
lch sag nur Quantencomputer. Und was ist jetzt dieses "Signieren"?
lch kann mit dem private key Nachrichten signieren. Das dient genau dem gleichen Zweck wie die Unterschrift unter einem Vertrag im realen Leben. Die Unterschrift bezeugt, dass ich dem Vertrag zustimme und wichtig ist dabei natürlich, dass niemand anderes meine Unterschrift erzeugen kann.
Um eine digitale Signatur zu erzeugen, nehmen wir unseren private key und eine Nachricht, die also signiert wird, und stecken beides in die entsprechende ECDSA-Funktion. Das Ergebnis ist die Signatur.

Ich sehe da nur Kauderwelsch
Ja, anschaulich ist so eine Signatur nicht. Das ist aber egal, denn jetzt kommt der Witz: Jeder kann jetzt nachprüfen, ob die Signatur wirklich von mir kommt, weil man zum Verifizieren nur den public key benötigt. Das geht dann so: Wir stecken die Nachricht, die Signatur und meinen public key in eine ECDSA-Funktion zum Verifizieren und finden heraus, ob die Signatur gültig ist.

Und weil’s so schön ist, können wir auch mal schauen, was passiert, wenn wir eine falsche Signatur verwenden, oder die Nachricht abändern:

Wo ist der Bezug zu Bitcoin?
Bei Bitcoin ist die Nachricht, die wir signieren wollen, eine Transaktion. Das heißt: Bitcoins gehen von Gustave zu Rosi. Damit die Transaktion gültig ist, muss sie von Gustave signiert werden. Das bedeutet, dass nur Gustave, der Besitzer des richtigen private keys, eine gültige Transaktion erzeugen kann. Nur er kann die Bitcoins ausgeben. In diesem Sinne ist der Besitzer des private keys der Besitzer der zugehörigen Bitcoins.
Bitcoins ausgeben? Wo gehen die denn hin? Das wirkt auf mich sehr unpräzise!
Eins nach dem Anderen, Dirk. Wir brauchen noch einen weiteren Schritt. Denn Bitcoin verwendet neben private und public key noch die sogenannte Adresse.

Bitcoin-Adressen
Prinzipiell würde schon alles funktionieren, auch ohne Adressen. Diese existieren als zusätzliche Sicherheitsebene. Die Idee ist, dass ich aus einem public key eine eindeutige Adresse erzeugen kann, ganz analog dazu, wie wir den public key aus dem private key erzeugt haben. An dieser Adresse kann ich dann Bitcoins empfangen.
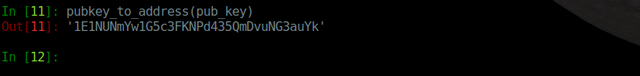
Auf Blockchain.info können wir die Adresse eingeben (oder den Link klicken) und die Geschichte sehen. Da wir ja außerdem den zugehörigen private key haben, können wir über die Bitcoins dieser Adresse verfügen.
Da sind ja schon Bitcoins drauf!
Da waren mal Bitcoins drauf. Das hängt damit zusammen, dass wir bei der Wahl des private key am Anfang etwas unvorsichtig waren. Wenn wir eine zufällige Zahl zwischen 1 und 1077 genommen hätten, hätten wir auch eine frische Adresse bekommen.
Ich lass das mal unkommentiert stehen.
Danke. Vielleicht ist das Erzeugen von private keys ein Thema für später. Wir schauen mal an, wie man aus einem public key die Adresse bekommt. Dafür stecken wir den public key in eine sogenannte Hash-Funktion.
Was so eine Hash-Funktion macht, lässt sich am einfachsten an Beispielen zeigen. In der ersten Spalte stehen ein paar Zahlen, in der zweiten Spalte das Ergebnis der Hash-Funktion, auch genannt: der Hash der ersten Zahl. Wer es ganz genau wissen will: Wir sehen die ersten 8 Ziffern vom SHA256-Hash im Hexadezimalformat ¯\_(ツ)_/¯.
| x | Hash(x) |
|---|---|
| 0 | 5feceb66... |
| 1 | 6b86b273... |
| 2 | d4735e3a... |
| 3 | 4e074085... |
Das sind zufällige Zahlen.
Es sind pseudozufällige Zahlen! Sie sind zufällig in dem Sinne, dass das Ergebnis - der Hash - scheinbar nichts mit der ursprünglichen Zahl zu tun. Sie sind pseudozufällig, weil für die gleiche Zahl immer ein und der gleiche Hash rauskommt. Das bedeutet, ich kann den Hash eindeutig bestimmen, aber nicht vom Hash auf die ursprüngliche Zahl schließen.
... was du oben mal die “Falltür”-Eigenschaft getauft hattest.
Bitcoin-Adressen bestehen neben dem Hash noch aus einer Versionsnummer und einer Prüfsumme und werden dann für bessere Lesbarkeit Base58-kodiert. Dieser letzte Schritt ist nicht weiter tiefsinnig. Man kann Zahlen eben unterschiedlich darstellen und Bitcoins Wahl fällt auf Base58, um doppeldeutige Zeichen wie o, O und 0 in Adressen zu vermeiden. Hier sehen wir beispielhaft ein paar altvertraute Dezimalzahlen und daneben die Darstellung als Hexadezimalzahl (Basis 16) und als Basis-58-kodierte Zahl.
| Dezimal | Hexadezimal | Basis-58 |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 1 | 2 |
| 2 | 2 | 3 |
| 9 | 9 | A |
| 10 | A | B |
| 16 | 10 | H |
| 58 | 3A | 21 |
| 1984 | 7C0 | bD |
Wer möchte, kann ja noch einmal unsere Adresse von oben anschauen und gucken, welche Zeichen da drin vorkommen und welche nicht. Damit sind wir fertig: Wir sind den kompletten Weg vom private key zur Adresse gegangen.
Wir können jetzt auch grob eine Transaktion zusammenbauen. Im einfachsten Fall ist das eine Adresse, wo die Bitcoins herkommen, und eine zweite, wo die Bitcoins hingehen. Das nennt sich dann erst einmal raw transaction.
Immer diese englischen Begriffe. Früher hätten wir einfach Rohtransaktion gesagt.
Schön. Der Besitzer der ersten Adresse benutzt jetzt seinen private key, um eine Signatur der raw transaction zu erzeugen. Die Signatur und seinen public key schreibt er dann dazu und aus der raw transaction wird eine signed transaction. Die wird dann im Bitcoin-Netzwerk verbreitet und damit ist der neue Besitzer der Bitcoins offiziell.
Das ist die Person, die den privaten Schlüssel zur zweiten Adresse hat.
Richtig! Nun soll es auch reichen. Hast du noch Fragen, Dirk?
Ich muss mir das mal in Ruhe anschauen. Einige Aspekte wirken auf mich wenig durchdacht!

Liebe Leser
Dies ist der erste Schritt, um mal etwas fundierter die Technologie zu verstehen, die hinter Bitcoin steckt. Ich hab das Thema Blockchain noch nicht einmal angerührt und es gibt schon diverse weitere Fragen und Aspekte, auf die ich direkt noch weiter eingehen möchte. Ist der private key wirklich einfach eine zufällige Zahl? Was wenn zwei den gleichen bekommen? Und: Wo sind da jetzt eigentlich meine Bitcoins genau?
Um weiterzuschreiben, bin ich auf Rückmeldung angewiesen: Zu technisch? Nicht technisch genug? Sind noch Dinge unklar? Ich freue mich auf Deinen Kommentar.
Ältere Artikel aus der Serie Kryptogeld verstehen
- Kevin lernt Bitcoin - Die Grundlagen
- Bitcoins kaufen - Über Bitcoin-Börsen
- Bitcoins sicher aufbewahren - Über Bitcoin-Wallets
Sehr gut, meeeeehr!
Einiges ist bekannt, aber Wiederholung ist der Freund der Porzellankiste.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Congratulations @gustave! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on any badge to view your own Board of Honor on SteemitBoard.
For more information about SteemitBoard, click here
If you no longer want to receive notifications, reply to this comment with the word
STOPDownvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
den Detaillierungsgrad finde ich gut, die Dialogform unterstützt das Lernen, eine Form - nicht in - wikipedia - aber eigenes wiki (gibts als leere SW) fände ich für mich hilfreich, wobei die Begriffe durchgängig und konsistent genutzt werden sollten (auch bei wechselnden Autoren).
Warum ist 5 keine Zufallszahl aber zB 10hoch66+257 ?
Die Seite blockchain.info wollte ich nutzen, um zu schauen wie es meinem bitcoin geht. Dort fand ich irgendwelche alten transaktionen, da hat jemand was rauf und runter gebucht. Hat das was mit meinem bitcoin zu tun, oder soll das ein Beispiel sein? Bei meinem mini Kenntnisstand kann ich auf dieser Seite nichts fragen und nichts erfahren. Deren Erläuterungen erscheinen mir rudimentär. Wo kann ich nachsehen wie es meinem bitcoin geht ? velleicht mag ich ihn ja verkaufen.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Hallo chris-iv! Danke für deinen Kommentar!
Diese Frage hat einen philosophischen Aspekt. Was ist eine zufällige Zahl? Die praktische Antwort auf diese Frage lautet: 5 ist keine gute Zahl, weil sie zu klein ist. Alle private keys aus kleinen Zahlen kann ich leicht reproduzieren - eben weil es vergleichsweise wenige sind. Ich brauche eine Zahl, die niemand errät, selbst wenn er mehrere Millionen Zahlen durchprobiert. Stell dir vor du wählst 100 Zahlen aus dem Bereich 1 bis 10^77: Wenn diese Zahlen in dem Bereich gleichverteilt sind, ist die Wahrscheinlichkeit, dass da eine Zahl kleiner als 10^20 rauskommt extrem gering (nämlich ca. 100 mal 10^-57 = 10^-55).
Der Link führt zu Blockchain.info, dort aber spezifisch zu allen Transaktionen, die auf der Adresse getätigt wurden, die mit dem private key 5 erzeugt wird. Wenn du wissen willst, wie es deinen Bitcoins geht, brauchst du nur deine Wallet-Software (die für dich die private keys verwaltet, aber auch die zugehörigen Adressen beobachtet).
Gut dass du fragst. Das hab ich in der Tat nicht erläutert.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
TMI - too much information :(
Da muss ich wohl noch einige male lesen...
Anyway: Danke für diese Zusammenfassung!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Gerne! Ich mache auch noch einmal auf die älteren Artikel aufmerksam - mit Kevin und Rosi, die leichter verdaulich sein dürften.
Wer aber Fortschritte in Richtung eines fundierten, technischen Verständnisses von Kryptogeld machen will, muss sich früher oder später mit der Logik hinter privaten Schlüsseln auseinandersetzen und noch mehr soll folgen.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
gerne mehr davon
wobei trocken Brot trifft es schon gut ist nicht für jederman geeignet und vermutlich auch nicht gedacht.
Teilweise musste man schon stellen mehrmals lesen um dran zu bleiben.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Wow, das sind seeehr viele Infos.
Ich werd mir das glaub ich mehrmals durchlesen müssen, um alles zu verstehen. Aber kanns mir ja abspeichern :)
Danke für deine Mühe.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Du kommst in dem Artikel sogar vor, ist aber ein bisschen versteckt. (Als zusätzliche Motivation für dich, alles zu lesen) ;)
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Hehe ja das habe ich gesehn, voll die witzige Idee :D
Irgendwann, bin ich wirklich Bitcoin Besitzer :)
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit