Der Gewinner

Wer wissen will worum es geht, der schaue hier
Gewonnen hat @yourfairy. Herzlichen Glückwunsch.
@yourfairy hat seine Lösung zwar nicht begründet oder gar bewiesen, aber da es keiner sonst getan hat, werde ich es nachholen.
Das Rätsel ist in der Szene recht bekannt. XD Allerdings habe ich es abgewandelt.
Ich hatte selbst mal das Vergnügen es zu lösen.

Die Auflösung

Zuerst habe ich mir überlegt, kann ich denn bei einer beliebigen Tür vorhersagen, ob sie auf oder zu ist. Nehmen wir z.B. die Tür 30. Welche Mitarbeiter kommen dort vorbei? Es kommt der 1., 2., 3., 5., 6., 10., 15. und der 30. daran vorbei. Das sind offenbar 8. Da das Spiel nach dem auf-zu Prinzip abläuft, ist diese Tür zu. Wie findet man aber raus wie viele vorbeikommen? Man braucht schlicht die Teiler zu bestimmen und deren Anzahl. Ist die Anzahl gerade ist die Tür zu und ist die Anzahl ungerade ist die Tür auf.
Das habe ich dann mit einigen weiteren Türen gemacht. Ich stellte fest, dass die meisten Türen zu waren. Ich fand fast keine offenen Türen. Aber ich kann ja schlecht alle Türen testen. Was macht man also? Ich reduzierte das Problem auf 20 Türen und ermittelte, welche Türen offen sind. Gedacht getan, es waren 1, 4, 9, 16. Jetzt beginnt die Suche nach einem Muster (1, 4, 9, 16 ...). Die meisten Menschen suchen jetzt nach einem rekursiven Algorithmus, d.h. wie komme ich durch den Vorgänger auf den Nachfolger. Das hat bestimmt auch @yourfairry gemacht. Das führt auch zum Ziel. Aber die eigentlich mathematische Frage löst das nicht. Warum geben diese Mathenerds eigentlich nie Ruhe? :)

Der Nerdteil

Als waschechter Nerd gebe ich natürlich auch keine Ruhe. Schaut man sich 1, 4, 9, 16 ... mal genau an stellt man fest, dass dies die Quadratzahlen sein könnten.

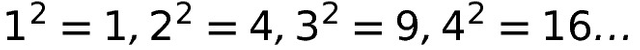
Jetzt kam für mich der eigentlich spannende Teil. Der Grund warum der absolut überwiegende Teil der Türen zu ist, scheint zu sein, dass Quadratzahlen gerade viele Teiler haben und nicht Quadratzahlen, d.h die ganzen übrigen Zahlen, ungerade viele Teiler haben. Das fand ich erst man ne steile Behauptung.
Um diese zu beweisen, schauen wir uns erst ein beliebige natürliche Zahl n an, die keine Quadratzahl ist.
Sei
,
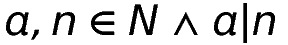so
.
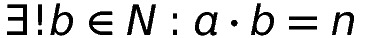Sei weiterhin
,
d.h. n ist keiner Quadratzahl.
Folglich ist
.
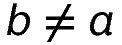Die Teiler von n kann man daher alle in Tupeln, d.h. Paaren (a,b) anordnen. Egal wie viele Teilerpaare n also besitzt, die Summe ihrer Teiler ist gerade.
Im Fall von 30 wären (1,30), (2,15), (3,10) und (5,6) die Teilerpaare.
Ein Quadratzahl besitzt auch Teilerpaare. Es gibt nur eine Ausnahme. Ihre Quadratwurzel lässt sich nicht als Paar (a,b) mit

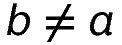
darstellen. Folglich besitzt sie neben den Paaren noch genau einen weiteren Teiler, daher ist ihre Teileranzahl ungerade. q.e.d.

Und weiter?

Natürlich könnte man das auch ganz anders beweisen. Ich hatte mir ja den Spaß gemacht einige Türen bzw. Zahlen zu überprüfen ( Teiler gezählt). Die Anzahl kam mir sehr willkürlich vor. 100 hat beispielsweise sehr viele Teiler, 35 wenige etc..
Man könnte sich also die Frage stellen: Kann man die Teileranzahl auch berechnen? In der Tat das geht. Keine Angst ich komme jetzt nicht mit sowas wie der Eulerschen Phi-Funktion um die Ecke.
Der Schlüssel liegt in der Primfaktorzerlegung. Diese ist bei jeder natürlichen Zahl eindeutig bis auf die Reihenfolge.
Für 60 schaut diese z.B. so aus:

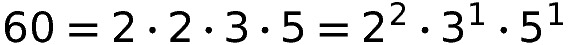
Jeder natürliche Zahl lässt sich also in die Form

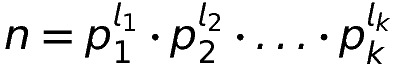
bringen.
Man kann sich daraus kombinatorisch herleiten, dass die Teileranzahl m gleich das Produkt der um 1 erhöhten Vielfachheiten der Primteiler ist.

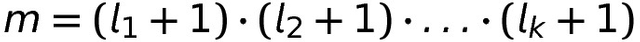
Für 60 wäre das :

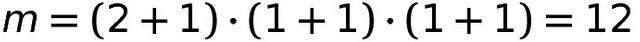
Würde man jetzt n quadrieren verdoppeln sich alle Exponenten und die Teileranzahl ist definitiv ungerade, da man ja jeden Exponenten um 1 erhöhen muss. Multipliziert man nur ungerade Zahlen, ist das Produkt wieder ungerade und damit auch die Teileranzahl m.
Das heißt im Umkehrschluss, dass jede primfaktorzerlegte Zahl mit nur geraden Exponenten eine Quadratzahl ist.
Ist mindestens ein Exponent ungerade, würde auch dieser Faktor um 1 erhöht und damit gerade. Multipliziert man eine Zahl mit einer geraden Zahl, ist das Produkt gerade. m ist somit gerade.

Quellen bzw. weiterführende Literatur:

E. Krätzel, Zahlentheorie, Deutscher Verlag der Wissenschaften

Die Bilder habe ich mit einem Latex to jpeg Converter erstellt: (http://www.sciweavers.org/free-online-latex-equation-editor)