Hallo liebe Steemians,
heute kommen wir zu meinem letzten Teil der Kryptographie-Reihe und ich möchte euch noch einen kleinen Einblick in ein spezielles Gebiete der Kryptographie einweihen.
Die Formalen Beweise sind in der Kryptographie oft gesehen und spielen weitestgehend ein paar Ideen bzw. Theorien durch. Gerade mit dem El-Gamal Algorithmus gibt es da drei interessante Ansätze.
Auch dieses mal handelt es sich lediglich um kurze Einblicke... Wer mehr dazu erfahren möchte und sich tiefer in die Kryptographie stürzen möchte, sollte sich im WWW dazu belesen :)
Wer die vorangegangenen Posts nicht mitbekommen hat, kann diese hier nachlesen:
Teil 1: Einleitung & klassische Kryptographie
Teil 2: Modulare Arithmetik
Teil 3: Symmetrische Kryptographie #1
Teil 4: Symmetrische Kryptographie #2
Teil 5: Asymmetrische Kryptographie #1
Teil 6: Asymmetrische Kryptographie #2
Teil 7: Asymmetrische Kryptrographie #3
Teil 8: Elliptische Kurven
Teil 9: Einweg Funktionen

Spezielle Gebiete der Kryptographie
Formale Sicherheitsbeweise
Idee (Reduktionsbeweis):
- Annahme: Es gibt einen erfolgreichen Angreifer A gegen das zu beweisende System
- Die Eingabe- & Ausgabewerte von A werden so umgeformt, dass ein bekanntes Problem der Kryptographie damit gelöst werden kann.
- Da das bekannte Problem in der Kryptographie als sicher gilt, muss auch das zu beweisende System sicher sein.
El-Gamal
Definition 45: Decisional Diffie-Hellman (DDH)
Gegeben: A=g^a, B=g^b, C=g^(ab) v g^x
Entscheide, ob c = g^(ab) mit einer anderen Wahrscheinlichkeit als 1/2 .
Definition 46: Indistinguistiablity - Chosen Plaintext Attack (INDCPA)
Das Spiel:
1. Angreifer wählt zwei Klartexte m0 und m1 und sendet an Simulator S
2. Der Simulator S wählt zufällig b ∈R{0,1} und verschlüsselt enc(m_b) = c
3. Angreifer bekommt c und gibt b'= 0 oder b'=1 zurück
4. Wenn b = b' gewinnt A
Definition 47: El-Gamal Sicherheit
El-Gamal ist IND-CPA sicher, wenn DDH sicher ist.
Beweisidee:
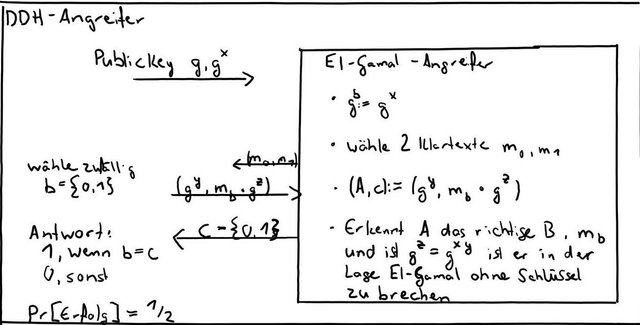
Da die Erfolgswahrscheinlichkeit nicht größer als 1/2 sein kann, ist der Reduktionsbeweis belegbar, und El-Gamal gilt somit als sicher.
Wie immer danke ich dir für dein Interesse. Wenn du Fragen zu einem Punkt hast, immer raus damit... Aufgrund der Komplexität des Themas ist es schwierig, dass in entsprechendem Umfang zu vermitteln, ohne den Rahmen komplett zu sprengen...
Natürlich bin ich immer froh über entsprechendes Feedback und natürlich auch ein Vote :)