Hallo Steem-Welt,
heute geht es weiter mit den ersten Anwendungen von den Grundlagen der letzten beiden Posts.
Da der Bereich der Symmetrischen Kryptographie etwas größer ist, werde ich das Kapitel in mehrere Posts unterteilen.
Wer meine ersten Posts verpasst hat, kann diese hier nachlesen:
Teil 1 : Einleitung & klassische Kryptographie
Teil 2 : Modulare Arithme*tik

Symmetrische Kryptographie
Symmetrische Chiffren ermöglichen das Sicherheitsziel Confidentiality (Vertraulichkeit).
Stromchiffren
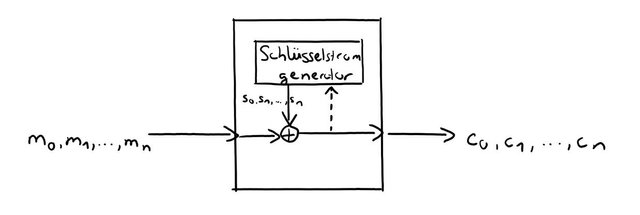
Bild: Stromchiffre synchron (& asynchron)
m - Klartext-Bits
c - Chiffrat-Bits
s - Schlüsselstrom (völlig zufällig generiert)
Asynchron dann, wenn s durch c beeinflusst wird
Definition 7: Stromchiffre
Eine Stromchiffre verschlüsselt Bits einzeln, dazu wird ein Schlüsselstrom (s0...sn) generiert,
der XOR mit dem Klartext verknüpft wird. (Bitweise Addition)
Bei synchronen Stromchiffren hängt der Schlüsselstrom nur von dem Schlüssel k ab.
Bei asynchronen Stormchifren zusätzlich von dem erzeugten Chiffrat.
Berechnung für mi, ci und si jeweils ∈{0,1}
Verschlüsselung: ci=encsi(mi) ≡ mi + si mod 2
Entschlüsselung: mi=decsi(ci) ≡ ci + si mod 2
Beispiel:
m = 0011 0011
k = 01 => si = 01010101
c = 0110 0110
0110 1111 0000 0101
0011 1010 0101 0000 58 80
Linear Feedback Shift Register
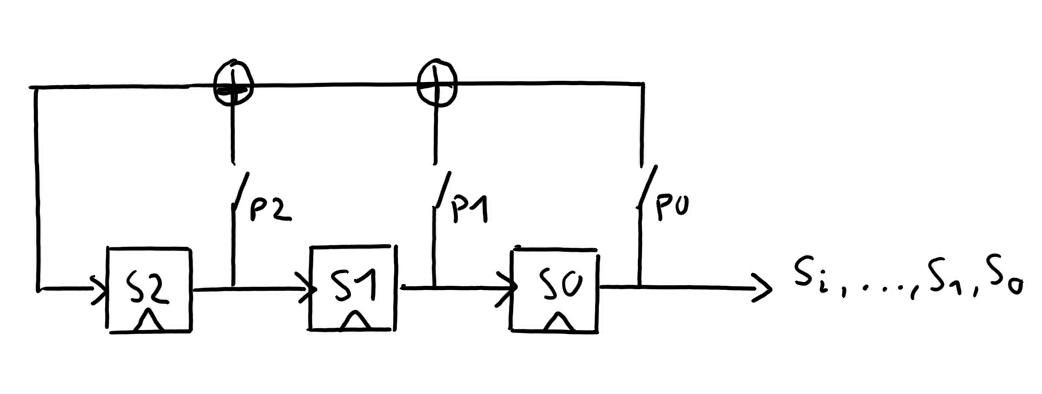
Bild: LSFR mit Grad 3
Funktion: Bausteine S1,S2,S0 sind FlipFlops, die einen Bit pro Takt "speichern" und nach rechts weitergegeben werden
Die Rückkopplung(Feedback) setzt sich aus dem Ausgabestrom der FlipFlops.
An S0 liegt der tatsächliche Schlüsselstrom
Definition 8: Linear Feedback Shift Register (LFSR)
Ein LFSR mit Grad m besteht aus:
- m getakteten Speicherbausteinen (Flipflops)
- Rückkopplungspfad
Mit jedem Takt wird ein Schlüsselstrombit si von dem LFSR generiert.
Beispiel: LFSR - Zustände der Flipflops und Output
Gegeben sind - p2 ist geschlossen (1)
- p1 ist offen (0)
- p0 ist geschlossen (1)
Berechnung zur Bestimmung des "überübernächsten" Bits am Eingang
s_i+3 ≡ 1 * s_i+2 + 0 * s_i+1 + 1*s_i mod 2
=> s_i+1 ≡ s_i+2 + s_i mod 2
Weiterhin gegeben sind Initialisierungswerte s2=1, s1=0, s0=1
Takt: FF2 FF1 FF0=s
0 1 0 1
1 0 1 0 Hinweis: FF2 wird zu FF1, FF1 wird zu FF0
2 0 0 1 FF2 wird durch XOR mit FF2 und FF0 des vorgängers gebildet
3 1 0 0
4 1 1 0
5 1 1 1
6 0 1 1
7 1 0 1
8 0 1 0
Definition 9: maximale Sequenzlänge
Die maximale Sequenzlänge eines LFSRs mit Grad m (Anzahl der Speicherbausteine) ist (2^m)-1.
Definition 10: Generelle Formel für Sequenz
Die generelle Forml für die Ausgabesequenz von LFSR mit Grad m:
Si + m ≡ ∑ pi * si+j mod 2 (von j=0, bis m-1)
mit si, pj ∈ {0,1}; ∀ i >= 0
Kryptoanalyse von LFSRs:
Geg: Grad m=3 des LFSR
2m Bits des Chiffrestroms si
Ges: Rückkopplungspfad p0, p1, p2
i=0: p2*s(-1) + p1*s(-2) + p0*s(-3) ≡ s0 mod 2
i=1: p2*s(0) + p1*s(-1) + p0*s(-2) ≡ s1 mod 2
i=2: p2*s(1) + p1*s(0) + p0*s(-1) ≡ s2 mod 2
i=3: p2*s(2) + p1*s(1) + p0*s(0) ≡ s3 mod 2
i=4: p2*s(3) + p1*s(2) + p0*s(1) ≡ s4 mod 2
i=5: p2*s(4) + p1*s(3) + p0*s(2) ≡ s5 mod 2
Dieses Gleichungssystem zeigt die Berechnungsvorschriften für das nächste Schlüsselstrombit , dass in den
ersten FlipFlop zurückgekoppelt wird, nicht die Ausgabe !
Die Ausgabe ist erst nach m+1 Schritten später sichtbar
Notwendige Bedingungen für eine maximale Sequenzlänge (2^m)-1
- Anzahl der Rückkopplungen (pi=1) ist gerade
- p0 = 1
Beispiel: Analyse LFSR mit Grad m=3
Gegeben: Grad m=3, 2m Ausgabestrom, si=(011100)
i=3 : p2*s2 + p1*s1 + p0*s0 ≡ s3 mod 2
i=4 : p2*s3 + p1*s2 + p0*s1 ≡ s4 mod 2
i=5 : p2*s4 + p1*s3 + p0*s2 ≡ s5 mod 2
=> (1) p2*1 + p1*1 + p0*0 ≡ 1 mod 2
(2) p2*1 + p1*1 + p0*1 ≡ 0 mod 2
(3) p2*0 + p1*1 + p0*1 ≡ 0 mod 2
<=> (1) p2 + p1 ≡ 1 mod 2
(2) p2 + p1 ≡ 0 mod 2
(3) p1 + p0 ≡ 0 mod 2
=> (1) + (2): p0 ≡ 1 mod 2
p0 -> (3): p1 ≡ 1 mod 2
p1 -> (2): p2 ≡ 0 mod 2
=> x³ + x + 1
Rivest Cipher 4 (RC4)
RC4 besteht aus 2 Algorithmen:
- Key scheduling algorithm (KSA)
Vorbereitung eines internen Feldes S[], in Abhängigkeit des Schlüssels
FOR i FROM 0 to 255
S[i]=i
END
j = 0
FOR i FROM 0 to 255
j = (j+S[i] + key[i mod keylength]) mod 255
SWAP(S[i], S[j])
END
- Pseudo-Random Generation Algorithm (PRGA)
Generieren von Schlüsselstrom X(jeweils ein Wort, Wortgröße W=8 bit)
i, j = 0
WHILE(Keystream required)
i = (i+1) mod 256
j=(j+S[i]) mod 256
SWAP(S[i],S[j])
X = S[S[i]+S[j] mod 256]
OUTPUT X
END
Die Ver- & Entschlüsselung geschieht durch XOR-Verknüpfung von Klartext (mi) mit dem Schlüsselstrom (Xi).
=> Ci = mi XOR Xi
Die Größe des Schlüsselraums von RC4(W=8Bit) ist die Anzahl der möglichen Permutationen von S[]:
256! ≂ 2¹⁶⁸⁴ ≂ 10⁵⁰⁷
Eine verbesserte Version, die die ersten 256 Output-bytes X verwirft, heißt Alleged RC4 (Arcfour)
Kryptoanalyse von RC4 am Beispiel von WEP
RC4 in WEP: C = RC4(iv||key) (m) ||: konkatenieren
Der initialisierungsvektor IV (24Bit) ändert sich mit jedem Paket und wird im Klartext übertragen: IV||C
Definition 13: Jenkins Krrelation
Robert J. Jenkins hat im Jahre 1996 folgende Beobachtung für S[ ] in der PRGA gemacht:
Pr(S[S[i]+S[j]]+S[j]=i) = 2/256
Die Wahrscheinlichkeit 2/256 ist doppelt so hoch, wie erwartet
Mit X(i-1) = S[S[i]+S[j] mod 256] wissen wir, dass
Pr(X(i-1)+S[j]=i)=2/256
<=> Pr(S[j]= i - X(i-1)) = 2/256
Definition 14:Angriff von Klein
Andreas Klein schlug 2005 folgenden Angriff auf WEP vor:
F(Key[0],...,Key[n-1], X(n-1)) = Key[n] = S⁻¹[n-X(n-1)-(S[n]+j(n-1) mod 256)]
S⁻¹ gibt Position im Array aus
Bekannt sind die ersten n Bytes des Schlüssels Key[], sodass die KSA bis zu dem Schritt n-1 simuliert werden können.
i(n) ≡ i(n-1) + 1 mod 256
=> i(n) ≡ n
j(n) ≡ j(n-1) + s[n] + key[n] mod 256
=> key[n] ≡ j(n) - (S[n] + j(n-1)) mod 256
j(n) fehlt für die Berechnung von key[n]. Mit Pr= 2/256 steht n-X(n-1) an Position j(n) in S[]
Wir suchen den Wert n-X(n-1) im Feld S(256+n)[] (Umkehrung der PRGA: Ŝ⁻¹[n-X(n-1)]).
Die Position (Index) ist dsa gesuchte j(n).
Wegen der geringen Wahrscheinlichkeit wird der Angriff auf viele WEP-Chiffrate durchgeführt und statistisch ausgewertet.
Beispiel:
WEP-Verschlüsselung mit key[0...7] = [12,111,28,107,226,211,232,247] und x2 = 251.
Gesucht ist key[3]
1. KSA Simulation
i0 = 0, j0 = 12 => Position 0 & 12 wird getauscht
i1 = 1, j1 = 124 => Position 1 & 124 wird getauscht
i2 = 2, j2 = 154 => Position 2 & 154 wird getauscht
i3 = 3, j3 = ?
2. Klein-Angriff (erfolgreich)
F(key[0],...,key[n-1], X(n-1)) = key[n] ≡ S⁻¹[n-X(n-1)] - (S[n]+j(n-1)) mod 256
=> F(12,111,28,251) = key[3] ≡ S⁻¹[3-X2]-(S[3]+j2)
≡ S⁻¹[3-251] -(3+154)
≡ S⁻¹[8] - 157 S⁻¹[8] ist NICHT IMMER =8 !!!
≡ 8-157
≡ 107 mod 256
Vielen Dank fürs Lesen! Wenn es euch gefallen hat, lasst mir gerne einen Vote und entsprechend Feedback da :)
Ausblick
Im nächsten Eintrag wird das Kapitel der symmetrischen Kryptographie dann fortgesetzt.