Hallo liebe Steemians,

heute geht es weiter mit der Kryptographie Reihe, und der Fortsetzung der symmetrischen Kryptographie
Wer die ersten Teile verpasst hat, kann diese hier nachlesen:

---

Teil 1: Einleitung & klassische Kryptographie
Teil 2: Modulare Arithmetik
Teil 3: Symmetrische Kryptographie #1

---

---

Blockchiffren

Defition 15: Blockchiffren

Eine Blockchiffre verschlüsselt Blöcke fester Länge, zb. 64 Bit. Der Klartext               
wird zerlegt und danach Block für Block verschlüsselt. Wenn der Klartext den 
letzten Block nicht vollständig ausfüllt, wird dieser aufgefüllt. (Padding)

Data Encryption Standard (DES)

Eigenschaften:
- Blocklänge: 64 Bit
- Schlüssellänge: 56 Bit ( + 8Bit Redundanz)
- interne Struktur ist eine Feistelchiffre
- 16 Verschlüsselungsrunden pro Block

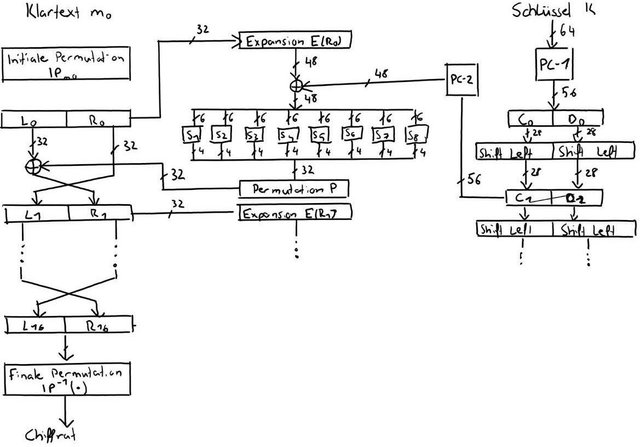
Funktionen :

- IP( )     8x8 Matrix  
- IP⁻¹ ( ) 8x8 Matrix
- PC-1 ( )  7x8 Matrix
- E( )  6x8 Matrix
- P( )  4x8 Matrix
- S Boxen 16x4 Matrix

Anmerkung: All die oben genannten Funktionen sind vorhandene, festgelegte Matrizen.
Diese hier alle aufzuführen, würde den Rahmen mehr als nur sprengen :D
Wer Interesse hat, findet die Daten alle im Netz.

Beispiel

101110 -> S-Box ->  1011
    1. und letztes bit gibt die Zeile an : 10 => Zeile 2
    die bits dazwischen geben die spalte an: 0111 => Spalte 7
=> An Position 2/7 steht die 11(dec) 
          -

Definition 16: Feistelnetzwerk

    Das Feistelnetzwerk lässt sich mathematisch beschreiben: 
        Li = R(i-1) 
        Ri = L(i-1) XOR f(R(i-1), ki)
        f Funktion (siehe Bild)

Entschlüsselung von DES

Die Entschlüsselung von DES unterscheidet sich von der Verschlüsselung nur durch eine veränderte
Teilschlüsselberechnung (Schlüsselfahrplan). Anstatt des Linksshifts im Transform-Block wird ein
Rechtsshift verwendet.

Transforms ohne Rechtsshift:        1
Transforms mit Rechtsshift 1Bit:    2, 9, 16
Transforms mit Rechtsshift 2Bit:    3, 4, 5, 6, 7, 8, 10, 11, 12, 13, 14, 15

Dadurch werden die Teilschlüssel in der Reihenfolge K16, K15, K14, ..., K1 gebildet.

Warum funktioniert das?

1. Die initiale Permutation IP wird durch die finale Permutation IP⁻¹ aufgehoben.
2. Das Feistel-Netzwerk ist invertierbar

Beweis:

Wir wissen von der Verschlüsselung, dass:
    L16 = R15
    R16 = L15 XOR f(R15,K16)
    
Und R16 steht auf der linken Seite, L16 steht rechts (Vertauschung)
Die Entschlüsselung beginnt mit K16 und  L0(=R16), R0(=L16=R15)
Die Invertiertung funktioniert , wenn L1=R15 und R1=L15 

L1 = R0 = R15
R1 = L0 XOR f(R0, K16) = R16 XOR f(R15, K16) = L15

Die Sicherheit von DES

• Differentielle Kryptoanalyse benötigt 2⁴⁷ Klartext-Chiffretext-Paare, um Schlüssel K zu finden.
• Lineare Kryptoanalyse benötigt 2⁴³ Klartext-Chiffretext-Paare, um Schlüssel K zu finden.
• Bruteforce-Angriff auf Schlüssel K(56Bit) benötigt mit Spezialhardware z.B.:
  Riviera S6LX150 (64 Cores) im Durchschnitt etwa einen Tag

=> DES gilt somit als gebrochen

3DES

Implementierung

c = DESK2(DesK1(m))                 2DES
c = DESk2(m XOR K1) XOR K3          DESX    
c = DESk3( DESk2 ( DESk1(m)))       3DES
c = DESk3( DES⁻¹k2( DESk1(m)))      3DES-EDE (Encryption-Decryption-Encryption)

Sicherheitsgewinn von mehrfache verschlüselung

2DES: c = DESk2( DESk1(m))

Meet-in-the-Middle Angriff:

1. Bruteforce (Aufwand: 2⁵⁶): c' = DESk1(m) und speichern Paare (c',k1) für alle k1
2. Bruteforce (Aufwand: 2⁵⁶): c' ? DES⁻¹k2(c) und vergleichen mit (c',k1) Paaren
Wenn Treffer, dann haben wir K1 & K2 gefunden. Der Aufwand ist 2⁵⁶ + 2⁵⁶ = 2⁵⁷ allerdings plus ein
Speicheraufwand von 2⁵⁶ * Blocklänge (64 Bit)

=> Die Sicherheit von 2DES mit 2 mal 56Bit Schlüsseln entspricht lediglich 57 Bit.

3DES-EDE:

Meet-in-the-Middle Angriff

1. Bruteforce (Aufwand: 2⁵⁶): c'=DESk1(m) und speichern Paare (c',k1) für alle k1
2. Bruteforce (Aufwand: 2¹¹²): c' ? DESk2( DES⁻¹k3(c)) und vergleiche mit allen (c',k1) Paaren
Wenn Treffer, dann haben wir K1, K2 & K3 gefunden. Der Aufwand ist 2⁵⁶ + 2¹¹² = 2¹¹² plus ein
Speicheraufwand von 2⁵⁶ * Blocklänge (64Bit)

Zusammenfassung: Die Sicherheit von 3DES-EDE mit einem 56 Bit-Schlüssel entspricht maximal 2¹¹² Bit

AES - Advanced Encryption Standard

AES wurde im Jahr 2000 als Nachfolger von DES veröffentlicht und hat folgende Eigenschaften:
Blocklänge: 128 Bit
Schlüssellänge: |k| = 128, 192, 256 Bit
in 32 Bit Words: L = |k|/32
Interne Struktur: Substitutions-Permutations-Netzwerk
Runden R = 10, 12, 14 angelehnt an die Schlüssellänge ( auch R = L+6)

Verschlüsselung (schematischer Überblick über den Rijndael-Algorithmus)

Bild

AES verwendet 2 konstante 2D-Byte-Arrays:
- S-Box 16 x 16 (SubstitutionBox): enthält Iversen in GF(2⁸)
- rCon 4x11 (Round Constant): erste Spalte = 2^(r-1) in GF(2⁸)

Defintion 17: KeyExpansion für 128 / 192 / 256 Bit

Folgende Schritte werden durchgeführt:
    1. Erzeuge eine Byte-Matrix W mit 4 Zeilen und 4(R+1) Spalten (=Wi)
    2. Trage Schlüssel k spaltenweise(!) ein
    3. Setze i auf erste freie Spalte Wi nach dem Schlüssel
        Bei 128 Bit Schlüssellänge: i=4
    4. Wiederhole Schritte solange, i<4*(R+1)
        a) tmp = W(i-1)
        b) Wenn i≡0 mod Li dann:
            + (1) rotiere tmp, (2) substituiere mit S-Box(SubBytes), 
              (3) XOR-verknüpfe das oberste Elemente der Spalte mit der Rundenkonstante rCon[i/L]
        c) Falls 256 BIt Schlüssel (L=8) & i≡4 mod L, dann:
            Substituiere tmp mit S-Box (SubBytes)
        d) Befülle neue Spalte Wi = W(i-L) XOR tmp 
        e) Inkrementiere i

Definition 18: SubBytes

Die Bytes eines Blocks(4x4) werden durch Werte aus der S-Box(16x16) ersetzt.
Das erste Nibbe des Bytes (0xab) ist die Zeile; a-> Zeile
Das zweite Nibbe des Bytes ergibt die Spalte;  b -> Spalte

Definition 19: ShiftRows

Zeilen eines Blocks werden byteweise nach links rotiert.
    Zeile 1: Keine Rotation
    Zeile 2: Rotation um 1 Byte
    Zeile 3: Rotation um 2 Bytes
    Zeile 4: Rotation um 3 Bytes

Definition 20: MixColumns

Ersetze jede Spalte Wi des Blocks durch das Produkt mit der folgenden Matrix im Rijndaal-Galois-Feld GF(2⁸) unter 
Verwendung des Polynoms: x⁸+x⁴+x³+x+1 (0x11b)

2   3   1   1   
1   2   3   1
1   1   2   3
3   1   1   2

Beispiel MixColumns

2   3   1   1   *   a1  = [2*a1 XOR 3*a2 XOR 1*a3 XOR 1*a4]
1   2   3   1   *   a2  = [1*a1 XOR 2*a2 XOR 3*a3 XOR 1*a4]
1   1   2   3   *   a3  = [1*a1 XOR 1*a2 XOR 2*a3 XOR 3*a4]
3   1   1   2   *   a4  = [3*a1 XOR 1*a2 XOR 1*a3 XOR 2*a4]

Definition 21: AddRoundKey

Block wird mit Rundenschlüssel(W(4r), W(4r+1), ...) der Runde r mit XOR verknüpft

Entschlüsselung von AES

Alle Schritte der Verschlüsselung werden in umgekehrter Reihenfolge angewendet.
Notwendig ist eine invertierte S-Box so wie die Umkehr von ShiftRows & MixColumns.

Multiplikation mit inverser MixColumn Matrix:
12 11 13 9
9 14 11 13
13 9 11 11
11 13 9 14

Die KeyExpansion läuft identisch, nur werden die Rundenschlüssel in umgekehrter Reihenfolge verwendet.

Die Sicherheit von AES

Die stärksten Angriffe (Biclique) ohne Vorraussetzung benötigen 2¹²⁶(128Bit), 2¹⁸⁹(192 Bit)
Der Angriff mit verwandten Schlüsseln benötigt 2¹⁷⁶ Schritte für 192 Bit, bzw 2⁹⁹ für 256Bit

Betriebsmodi von Blockchiffren (Operation Modes)

Definition 22: Electronic Codebook Mode (ECB)

Jeder Block wird unabhängig voneinander verschlüsselt:
Verschlüsselung eines Blocks mi für alle i>=0, ci=enck(mi)

Eigenschaften

• Die Verschlüsselung eines Blocks führt immer zum gleichen Chiffrat

Beispiel: Angriff auf ECB

Fremde Überweisung: 500.000 € von Edith an Christian
                    0x1111 | 0x2222 | 0x3333
Ihre Überweisung 1: 3,50 € an Tante Emma
                    0x1337 | 0x082A | 0xCAFE 
Ihre Überweisung 2: 3,50 € an Onkel Gerd 
                    0x1337 | 0x987 | 0xCAFE
Angriff:            500.000€ von Christian an mich
Neue Transaktion:   0x2222 | 0x1337 | 0x3333

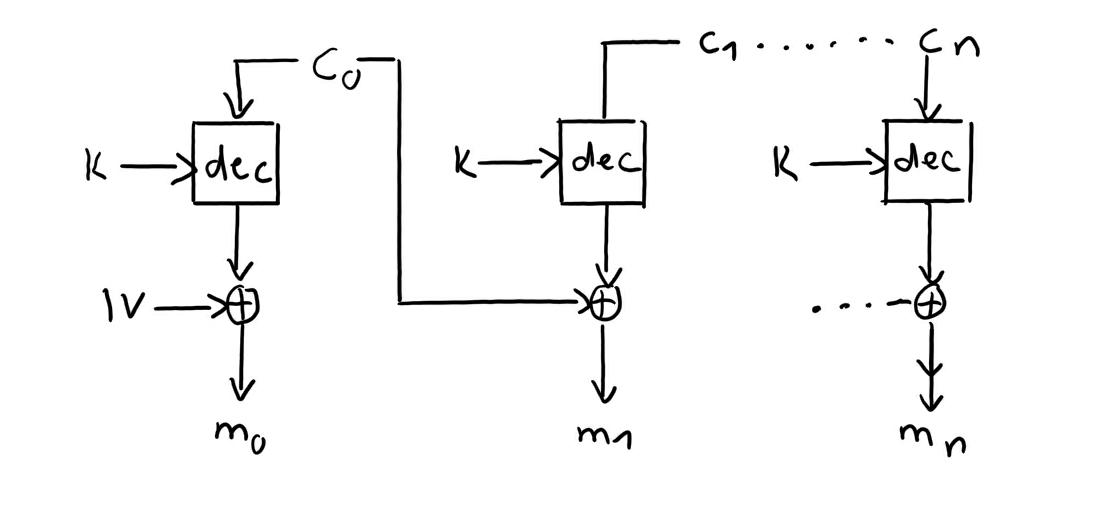
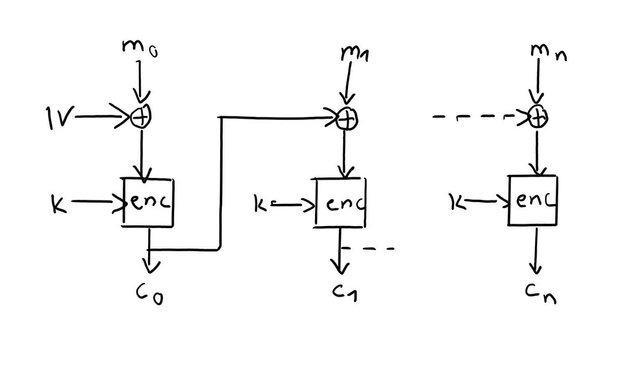
Definition 23: Cipher Block Chaining Mode (CBC)

Verknüpfung des Klartextblocks mit vorherigem Chiffreblock, dann Verschlüsselung

Funktionen

Verschlüsselung

c0 = enck(m0 XOR IV)
ci = enck(ni XOR ci-1)) 

Entschlüsselung

m0 = deck(c0) XOR IV
mi = deck(ci) XOR ci-1

Eigenschaften
Spezielle Fehlerfortpflanzung ^ = EinBitFehler ~ = MehrbitFehler
- 1 Bit Fehler : ^c0
~m0 = deck(c0) XOR IV Ändert sich ein Bit wird nach dem enc/dec der ganze Block anders
^m1 = deck(c1) XOR c0
m2 = deck(c2) XOR c1

Bei diesem Fehler wird der erste Block komplett zerstört, der zweite Block hat ein gekipptes Bit,
und ab dem dritten ist die Verschlüsselung wieder korrekt.

Definition 24: Cipher Feedback Mode (CFB)

        Verknüpfung des Klartextblocks mit mit Verschlüsselung des letzten Chiffreblocks.
        Der CFB Modus erzeugt eine Stromchiffre aus einer Blockchiffre.

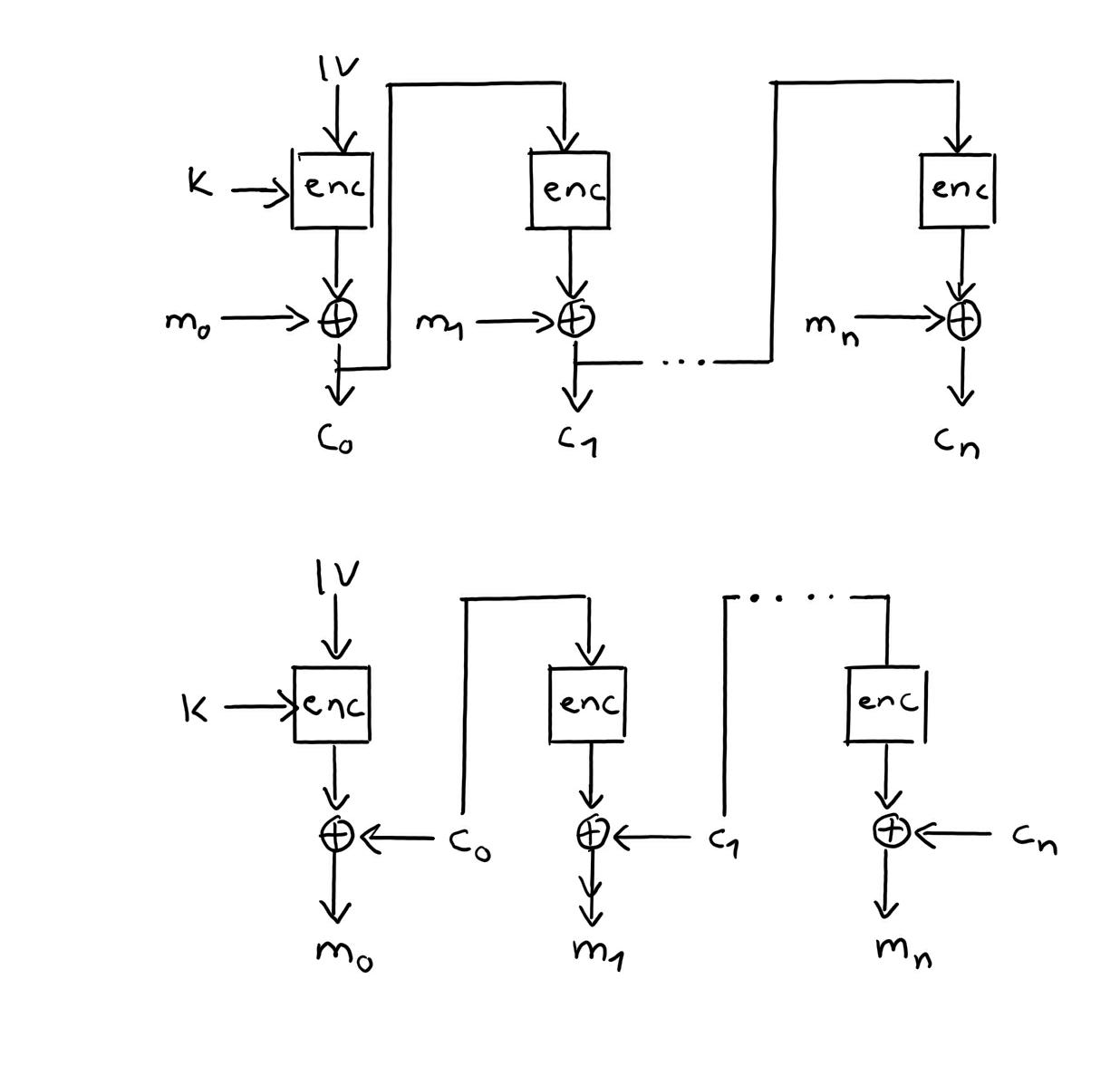
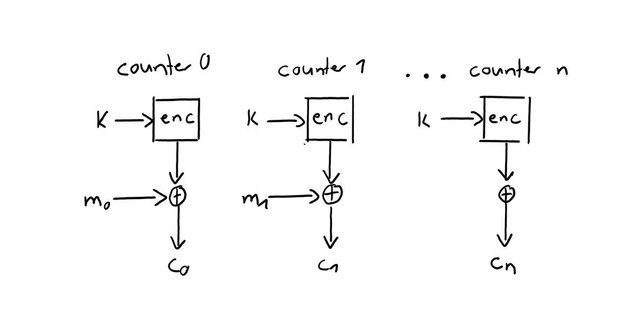
Definition 25: Counter Mode (CTR)

Verknüpfung des Klartextblocks mit Verschlüsselung eines Counters.
Initial besteht der Counter oft aus einem bekannten Zufallswert, der für jede Operation 
inkrementiert wird.
Der Counter Modus erzeugt ebenfalls eine Stromchiffre.

---

Vielen Dank für eure Aufmerksamkeit!
Wenn es euch gefallen hat, lasst mir gerne ein Upvote da und natürlich gerne auch Feedback :)

---