DTube: Integral of sin^3(x), sin^3(ax) with substitution and trigonometric identity

In this tutorial, we'll work through 2 different approaches to solving the integral of sin³(ax). Now, there maybe more ways of approaching this problem, but these were the most obvious to me.

Using a substitution
Using a trigonometric identity

Let's have a go...

1. Method of substitution

The idea behind integration by substitution is to apply the chain rule in reverse. So we want to write the integrand...

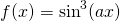
...in the form of...

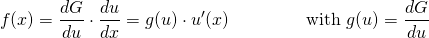
So, if we break up the integrand sin³(ax) as follows...

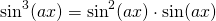
...and apply the Pythagorean Identity to the sine-squared term, we have...

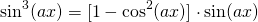
Now, if we let the function u(x) = cos(ax), we can make the u-substitution, and integrate both sides of the equation...

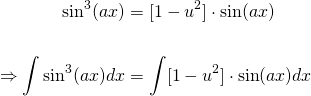
We cannot integrate the right-hand side yet, because we still have functions of x there. But if we also take the derivative of u with respect to x, and separate the differentials...

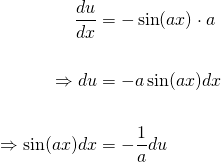
Now we can replace the trailing sin(ax)dx with -(1/a)du and turn the right-hand side into a simple power integral...

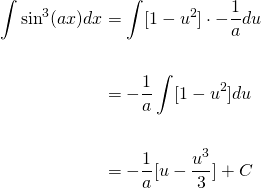
Great! We solved the integral and got the answer in terms of u. Now, we need to substitute cos(ax) back in to get the complete solution...

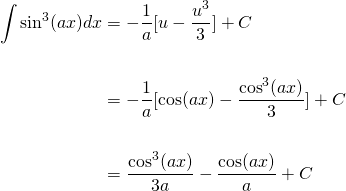
So, we have achieved the solution with the method of substitution. What about the second approach?

2. Trigonometric Identity

The idea behind using trigonometric identities is to reduce the power of the integrand to an expression that has no exponents, so that we are able to use a standard integral to find the solution.

We have the triple-angle formula...

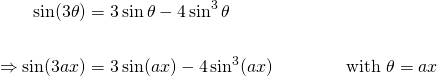
Rearranging to make the sine-cubed term the subject and then integrating both sides...

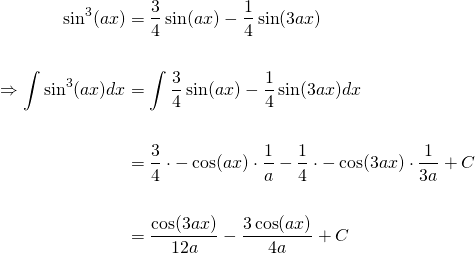
Alright, now comparing the answers for methods 1 and 2...

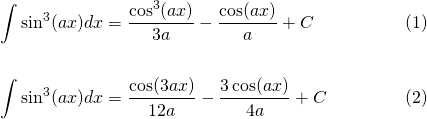
...are equations (1) and (2) equal? Well, if you use the triple-angle formula...

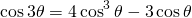
...and rearrange for the cosine-cubed term and substituted this into equation (1), you'll find that the answers derived from both methods are indeed equal!

Thanks for watching. Please give me an Upvote and Resteem if you have found this video helpful.

Please ask me a math question by commenting below and I will try to help you in future videos.

I would really appreciate any small donation which will help me to help more math students of the world.

Tip me some DogeCoin: A4f3URZSWDoJCkWhVttbR3RjGHRSuLpaP3
Tip me at PayPal: https://paypal.me/MasterWu

► Watch on DTube
► Watch Source (IPFS)