Basic information.
The use of distinguishing equations, it allows us to have a clearer explanation, of how obtaining an analytical and graphic solution, of the above mentioned equations; taking in account, in the majority of the cases in the equations of supply and demand, they are determined by linear equations. Also we have the case, of the use of the formula of the second grade, which serves us to give solution, clearing the terms up to leaving the independent "X".
In reference to the law of demand; it consists, when the consumers buy or it demands goods and services to the biggest possible quantity, at the minor price; and the law of offer consists, of offering the biggest possible quantity of goods and services at the biggest possible price. As soon as. to the balance of market; this one happens, when there cross two curves of demand and offer, this owes that it comes to a point of the market, that the quantity offered as goods and services is an equal demanded quantity, under a level of price of balance.
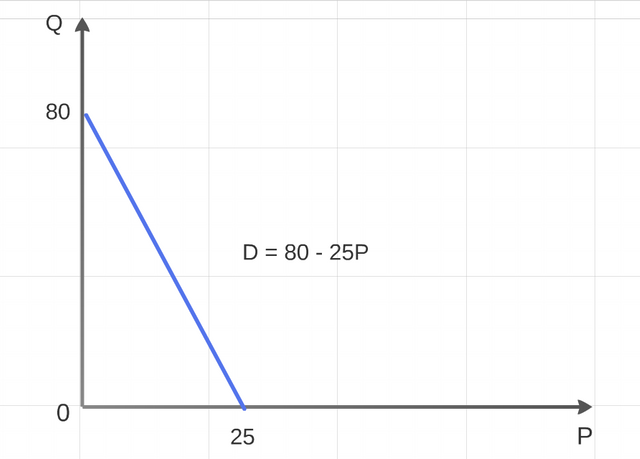
Figure 1. (Prepared for @chetoblackmetal)
Behavior of the claimant or buyer, on a market having the following linear equation.
D = 80 – 25P, where P is the price.
 | Considering the function of demand x=f (p), where the quantity of demand x of an article, it depends only on the price P on the article, if the price P and the demanded quantity x is related to the following equation. |
|---|---|
| Datos | P= (300/x+3) – 8 |

We have that:
P = (300/x 3) – 8; since, we are going to work in x=f (p), we realize the following thing:
P = (300/x 3) – 8
P 8 = 300/X 3
X = (300/P 3) - 8
For x=f (1), we have that:
X = (300/1 3) – 8
X = 67
For x = f (2)
X = (300/2 3) - 8
X = 52
For x = f (3)
X = (300/3 3) - 8
X = 42
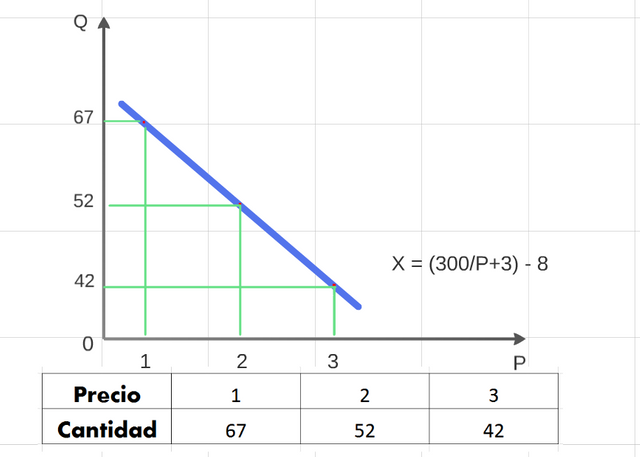
Figure 2.(Prepared for @chetoblackmetal)
Next I show the following exercise, where I explain the breakeven.
 | To find the breakeven of the market, if the equations of the supply and demand of a product, they are the following equations: |
|---|---|
| Datos. | P= x/30 + 5 y P= 3000/x. |

We have that:
P = x/30 5 and P = 3000/x.
x/30 5 =90000/x
x 5 = 90000/x
(x 5) x = 90000
The Xth ² 5x-9000 = 0
On having solved the following equation of the second grade:
X1 =-300 √5 ²-(1 (4) (-90000)) / 2 (1)
X1 =-300 √360025/2
X1 =-300 600 / 2
X1 = 300
An hour according to the equation:
P = 3000/x
P = 3000/300
P = 100
With the values of x1 = 300 and P = 100 is the balance, giving the following coordinated one (300,100).
He wants to say to us, that the price of balance of the market of 100, 300 quantities offer of x well; where, 300 units at the same time, it is demanded or is bought; because it is, the same quantity offered on the market.
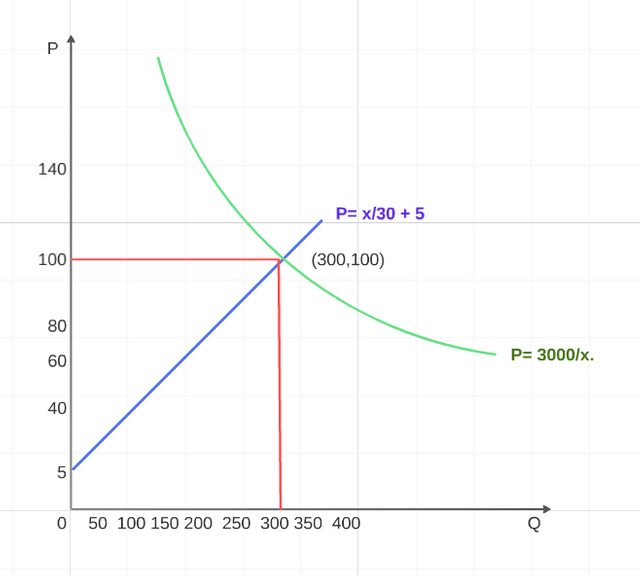
Figure 3. (Prepared for @chetoblackmetal)
The following exercise, there will be tackled the price that maximizes the entire benefit, according to the producers.
 | Where x is the quantity of units of the demanded product; and P unit price, and the cost of production of every sold unit is 30 Bsf. What is the price that maximizes the entire benefit of the producers, and how many voucher this maximum benefit?, being the product the banana |
|---|---|
| Datos. | : The following equation is had: P + x/2 + 60 = 0. |
We have the following thing:
The revenue we represent her in the following equation:
XP – 30X = the Xth (P – 30)
Taking in account, the demanded quantity is:
P X-60/2=0
X - 60 =-2P
X =-2P 60
To obtain the entire benefit it is:
B = (-2P 60) (P – 30)
B =-2P ² 60 P – 1800
We apply the equation to resolve, an equation of the second grade:
B = - 60 - 60 ²-4 (2 (-1800)) / (-2 (2)) we take the option with the sign (-); since, the result gives: positive (-/-=), or also we can say, it is a reached maximum, since the coefficient in P ² is negative.
B =-60 - √3600 14400 /-4
B =-60 - 134, 16 /-4
B =-194,16 /-4
B = 48,54
Now then, for the maximum reached value of the entire benefit:
B = 60 ² - 4 (-2) (-1800) / (-4 (2))
B = 3600 - 14400 /-8
B =-10800 /-8
B = 1350
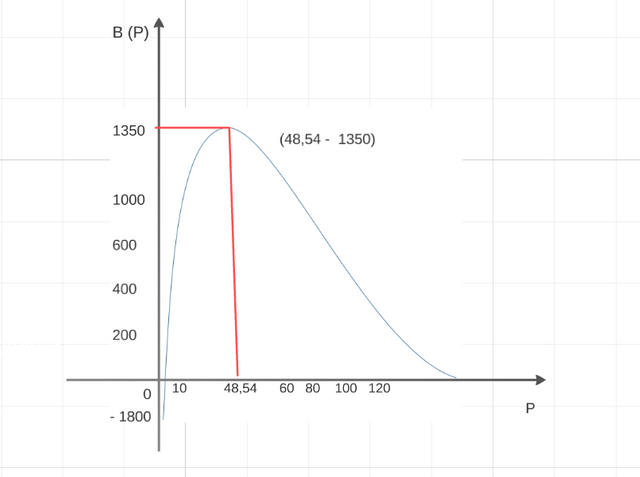
Figure 4.(Prepared for @chetoblackmetal)
The obtained resulto, it shows us for every sold unit 30 Bsf, the maximum obtained benefit is 48,54; with an entire benefit of the selling of banana of 1350.

Beyond the economic world; it is necessary to recognize that the mathematics, are a very fundamental tool, to give restored to the phenomena of the reality; to have an analysis, which they show by means of the experimental facts; to have a better scientific knowledge that one adapts to any need; it is going to serve us, to generate information about new models of application of the mathematics.
In another order of ideas, also he allows us to analyze the algebraic solution; to determine, if the obtained value answers to the conditions of the problem. It is important to know, what type of incidence we have when we apply the mathematical knowledge, to the moment to construct models or theorems.
BIBLIOGRAPHICAL REFERENCES AND RECOMMENDED LECTURES.
Mathematics for Administration, Economy, Social Sciences and of the Life ”
HAEUSSLER * PAUL.
Analysis of a real variable for Celso Martínez Carracedo, Miguel A. Sanz Alix (1992).
Introduction to the mathematical analysis for Joaquín M. Black-bellied sandgrouse (1993).
Mathematics for the economy and the finance for Martin Anthony, Norman Biggs (2002).
Introduction to the mathematics for the economy for Francisco José Martínez Estudillo (2005).
Mathematics for the XXIst century for Sergio Macario Vives (2006).
Mathematics for the economy and the company for Susana Calderón Montero, María Lourdes Rey Lamb (2012).
Differential calculus for Alberto Camacho Ríos (2012).

Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit