Einstein fue más allá del establecimiento de la equivalencia entre sistemas no inerciales y sistemas inerciales con gravedad.
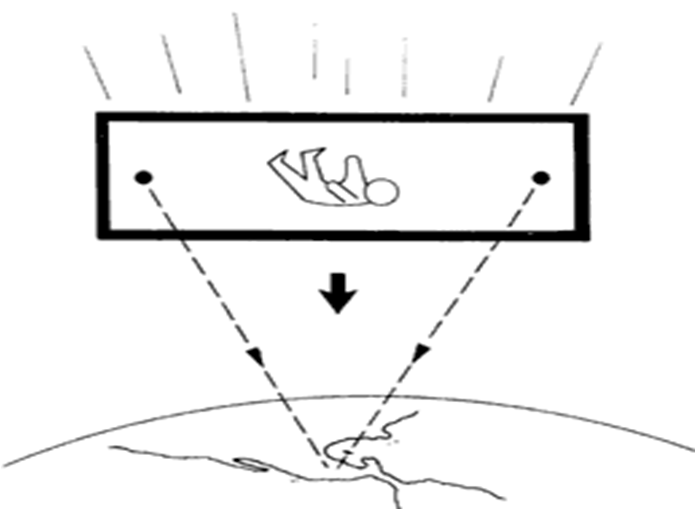
Para entender de manera sencilla a dónde llegó Einstein con el Principio de Equivalencia, se analizará el ejemplo de la caja en caída libre, pero esta vez se supondrá que la caja es lo suficientemente grande como para hacer el siguiente experimento:
Colóquense dos canicas en cada extremo del compartimento, como se indica en la figura anterior. Como las canicas se hallan también en caída libre permanecen fijas flotando para los ocupantes de la caja. Sin embargo, las trayectorias de ambas no son exactamente rectas paralelas, sino rectas que convergen al centro de la Tierra. En consecuencia, vistas desde la caja, las dos canicas no están estrictamente fijas, sino que parecen acercarse lentamente una a otra. Este efecto casi imperceptible no ocurriría si la caja estuviera en el espacio extraterrestre, lejos de todo influencia gravitacional, ya que las dos canicas permanecerían exactamente donde se colocaron.
El experimento anterior implica que la equivalencia entre sistema inercial y sistema en caída libre debe formularse con más precisión: Los dos sistemas son equivalentes en una región pequeña del espacio, pero pueden distinguirse uno del otro si se realizan experimentos físicos sobre distancias suficientemente grandes. Esta comprobación condujo a Einstein a relacionar la gravitación con las propiedades geométricas de una superficie. Por ejemplo, se sabe que la Tierra es redonda, pero su curvatura no se manifiesta en una región pequeña; a escala humana, el planeta parece plano y es sólo sobre distancias de varios cientos de kilómetros que los efectos de la curvatura se vuelven apreciables. Si se trazan dos rectas paralelas sobre la superficie terrestre, estas rectas permanecen paralelas inicialmente manteniéndose constante la distancia entre ellas; pero si las rectas se prolongan cientos de kilómetros empezarán a converger debido a la curvatura de la Tierra, y acabaran por unirse en algún punto . Las rectas trazadas sobre la superficie de la Tierra son más bien segmentos de círculo; es sólo a escalas pequeñas que parecen rectas. El concepto de recta pierde su sentido sobre una superficie curva y es más preciso referirse a curvas de longitudes mínimas o geodésicas: sobre una superficie plana, la recta es la curva de mínima longitud entre dos puntos dados, pero sobre la superficie de una esfera la curva más corta entre dos puntos es un segmento de círculo.
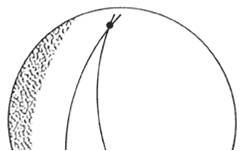
Dos "paralelas" trazadas sobre la superficie de la Tierra, y que terminan por unirse debido a la curvatura de ésta, recuerdan las trayectorias de las dos canicas en la caja que cae.
Ahora bien, las dos "paralelas" trazadas sobre la superficie de la Tierra, y que terminan por unirse debido a la curvatura de ésta, recuerdan las trayectorias de las dos canicas en el elevador que cae. En el primer caso, se tiene un efecto debido a la curvatura de una superficie, mientras que en el segundo caso se manifiesta una fuerza gravitacional. El primer efecto es geométrico y el segundo gravitacional. Una superficie curva parece plana en una región suficientemente pequeña, y del mismo modo una fuerza gravitacional no es detectable en un vehículo de dimensiones reducidas y en caída libre.
Las geodésicas son las curvas de menor longitud sobre una superficie curva.
Todas estas analogías condujeron a Einstein a la conclusión de que la fuerza gravitacional puede interpretarse como un efecto geométrico. Sólo que, a diferencia de la superficie terrestre, que es un espacio curvo en dos dimensiones, pues se necesitan dos números para indicar cualquier posición sobre ella (longitud y latitud), en la teoría de Einstein el espacio-tiempo es curvo y la gravitación es la manifestación de su curvatura.
No fue sino hasta la segunda década del siglo XX cuando Einstein llegó a la conclusión de que el espacio- tiempo en el que vivimos es un espacio curvo de cuatro dimensiones. Einstein publicó la versión definitiva de su teoría de la relatividad general en el número de noviembre de 1915 del Boletín de la Academia de Ciencias de Berlín, en plena primera Guerra Mundial. La esencia de la teoría de Einstein es que la masa de un cuerpo deforma el espacio-tiempo a su alrededor. En ausencia de masa, el espacio-tiempo es plano y una partícula se mueve en línea recta porque nada influye sobre su trayectoria, pero en presencia de una masa gravitante, el espacio-tiempo se curva y una partícula se mueve a lo largo de una geodésica. De acuerdo, con esta interpretación de la gravedad, un planeta gira alrededor del Sol porque sigue una trayectoria geodésica en el espacio-tiempo deformado por la masa solar. En la teoría de la gravitación de Newton, se puede calcular la atracción gravitacional ejercida por una distribución dada de masa por medio de una ecuación matemática. En la teoría de Einstein, se calcula la curvatura del espaciotiempo, pero la situación es bastante más complicada porque no sólo la masa sino también la energía ejercen una acción gravitacional. En su artículo de 1916, Einstein dedujo la ecuación matemática que relaciona la geometría del espacio-tiempo con la distribución de masa y energía: esta fórmula se conoce como ecuación de Einstein y es la base de la relatividad general. Si los físicos no se habían percatado antes de Einstein de que el espacio es curvo es porque la gravedad de la Tierra y del Sol induce una curvatura extremadamente leve. La situación es semejante a la de los hombres antiguos que creían que la Tierra era plana, ya que su curvatura es imperceptible a pequeña escala.
NOS VEMOS EN LA TERCERA PUBLICACIÓN CON EL tag EDUCACIÓN