Hey everyone!
How's everything going? I sincerely hope each and everyone of you had a great time during the weekend. To me weekends are all about family and friends. And a little bit of Geodesy maybe? A new week means another opportunity for a brand new beginning. As you've probably realized by now, I'm back in business with another scientific blog. Oh, no! Not again! I'm not here to play around though, so let's get this started!
As promised, this is my third and final blog regarding this Introduction to Geodesy, which is the scientific field of observing and measuring the shape and size of the Earth. This time I'd like to take the chance to share advanced technical information regarding our planet's gravitational field and significant historical information concerning Geodesy and geodetic problems of the ancient times. I will also share general introductory information regarding astronomical coordinates, so stay focused!
I feel the need to clarify once again that these are still introductory posts, meaning that I will do my best to keep things simple and fun. That basically means that I will share some general information with a pinch of humour. Sorry, not sorry. There's a high chance of learning a thing or two by reading this post, so stay focused!

Image Source: pixabay.com
History
The first geodetic problems recorded occured in the ancient times. Civilizations residing in Mesopotamia (Sumerians, Babylonians, Assyrians, ancient Acadians), the middle East and Egypt possessed knowledge of theoretical geometry and practical astronomy, even prior to the rise of the ancient hellenistic age. A specific sort of land register was developed and kept by civilizations residing close to the Nile area, which was aiming to aid development in agricultural activities. Those ancient civilizations' technological advancement and level of scientific knowledge can be comprehended by taking a look at the pyramids' geometry. The existence of agglomeration projects regarding big cities of the ancient times, as well as elements utilized to keep track of time such as solar clocks prove that those ancient civilizations were probably a lot more advanced than we actually realize nowadays. Such advanced knowledge wasn't available to the public though, as it was basically being kept secret and suppressed mostly by priests. The Greeks possessed such knowledge even before the classical ancient times and could define city boundaries with accuracy. Important figures in greek history, including philosophers and scientists of the ancient times, traveled towards Egypt and the middle East in order to interact and exchange scientific information with citizens of those thriving civilizations. This exchange of information influenced civilizations and scientists in a productive manner and induced further scientific advance. Plato will always be remembered for stating that whenever the greeks borrowed knowledge from non-greeks they turned it into perfection.
One of the most common features and problems of the pre-hellenistic period was the deification of natural phenomena. People would perceive natural disasters such as earthquakes, volcano eruptions or even thunderstorms as the product of the gods' wrath. As a result scientific development was slowed down significantly by the mass adoption of such beliefs, until the greeks demystified technical knowledge by setting the foundations of modern science and producing technical information. This attempt was inspired by the desire to comprehend and interpret various natural phenomena that were being observed. Τhe first practical indicators of the Earth's spherical shape were observations made by sailors, as they started noticing that points of higher altitude on the land's surface where the first ones to become visible when approaching land. Likewise, observers situated on land would first notice the masts of vessels approaching in the horizon. Other practical indicators were simple observations regarding the Earth's circular shadows casted on the lunar surface, as well as the round shapes of the Moon and the Sun which implied that the Earth was shaped similarly. Thales of Miletus (624BC. - 546BC.) ignored all theories describing a disc shaped Earth surrounded by oceans and believed the Earth had a round shape as well. Thales set the foundations of modern geometry. He was the one to calculate and determine that a year consists of 365 days. Thales also proved that the Earth's four seasons aren't equal in terms of duration.

Image Source: pixabay.com
Anaximander of Miletus (610BC. - 546BC.), who was Thales' colleague, was the first one to ever build a map of the known world by utilizing a cylindrical projection. He also produced a map of the sky and a solar clock. Anaximander was the first one to ever use a set square in his drawings. However, the first one to ever assume that the Earth is in fact revolving around the Sun was Pythagoras of Samos (570BC. - 495BC.), who was running a famous school of science in Crotone, Italy. He made the assumption that all known celestial bodies revolve around a specific point in space, in a particular manner which can be described using mathematical equations. Pythagoras was basically the first one to ever express the notion that the Earth is not motionless in the first place. During the same year, Eupalinos of Megara (575BC. - 495BC.) who was an amazing ancient greek engineer, managed to design, engrave and conclude an astonishing technical construction, which is rather amazing especially taking into consideration the fact that there was no technological equipment available. He managed to construct a 1036m long tunnel for water supply purposes in Samos by digging through the mountain at an altitude of 300m. The drilling process started on both sides of the mountain and accomplished an abstention of only 1.8m at the meeting point. What the fact? This specific technical construction has baffled scientists and researchers until nowadays, particularly because of the absence of official papers regarding the engraving and construction process.
Plato of Athens (428 BC. - 348 BC.) was not an astronomer, however he did accept Pythagoras' theory of the spherical Earth. As a philosopher, Plato mentions in his writings that practical scientists in the field of geometry have to realize that any geometrical shapes observed are in reality projections of each one of those ideal geometrical objects. Following Plato's train of thought can be a nightmare. He actually believed that everything observed is actually a graphic representation of reality which is projected on this 3D realm. Despite being a philosopher he was one of the first to realize and state that the scientific field of astronomy should be about the definition and comprehension of the motions of celestial bodies observed, as well as the definition of the exact orbital speed and shape of celestial bodies. These notions expressed by Plato actually assisted scientists to determine and specify more precise 3D models in an attempt to reach accurate conclusions. Conclusions reached and applied in pursuit of scientific truth. Galileo Galilei (1564 - 1642) stated that his beliefs regarding the way our solar sytem's bodies move were inspired and fueled by Plato's writings.

Image Source: pixabay.com
The Earth's Gravitational Field
Every object that is rotating along with the Earth is subject to the planet's gravitational field and the spin's centrifugal force. Τhe resultant force pulling objects towards the Earth's center of mass is known as gravitational force or gravity. Its magnitude (g) is often called gravity as well. This magnitude (g) is measured in m/sec^2 (S.I.) and also in gal (1 gal = 10^-2 m/sec^2), named after Galileo Galilei. Gravimeters are instruments utilized to make accurate measurements of gravity values achieving precision of μgals (1 μgal = 1 x 10^-6 gal). That's great precision. We always need to keep in mind that gravity changes according to an observer's change of position, for instance g equals 9.780m/sec^2 on the Equator while its value on the poles equals approximately 9.830m/sec^2, which is 0,5% greater. An average value of roughly 9,806 is acceptable. Just for the fun of it I will proceed to mention how gravity on the Sun is actually 28 times greater than on Earth (28g), while gravity on the Moon is 6.3 times smaller than on Earth (0,15g). Furthermore, Mars has a gravity of 0.4g, Pluto's gravity equals 0.059g and Jupiter's gravity equals approximately 2.54g.
Gravity voltage (W) concerning specific points in space is highly relevant to a point's position and is calculated using the formula : W = V + Φ , V & Φ being the attractive and centrifugal voltage respectively, g = gradW. The objective of determining the value of W is best served by the scientific field of Natural Geodesy. The development of 3D models and methods of precisely calculating and defining the Geoid's shape is one of this scientific field's main concerns. For the simplification of mathematical calculations W is analyzed into two different parts : W = U + T. The value of U is then calculated with the use of analytical equations according to the 3d model utilized, however the calculation of the value of T depends on parameters and measurements made regarding the Earth's gravitational field. It is therefore calculated: W ~ GM/R = (3986005 x 10^18 m^3/s^2)/6371000m = 62564825m^2/s^2. I'm serious. The sum of all points situated in different areas of equivalent gravitational force creates mathematically complicated surfaces of significant interest, as no energy whatsoever is demanded or spent on such surfaces; for instance water doesn't flow and remains motionless. In other words, every motionless particle of water in the ocean is part of such a surface at that specific point in time.
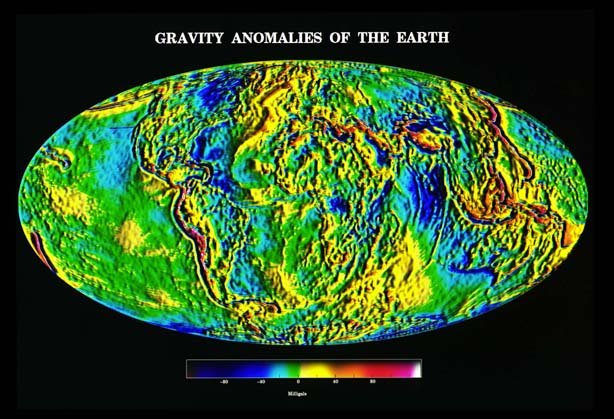
Gravity Anomalies of the Earth./ Image Source: denali.gsfc.nasa.gov
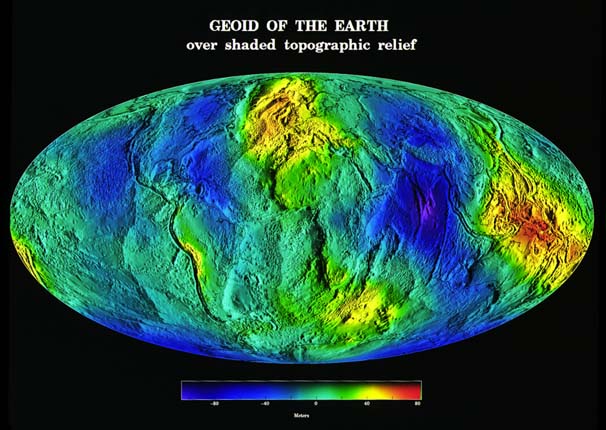
Geoid of the Earth./ Image Source: denali.gsfc.nasa.gov
Elementary transpositions of points located on the Earth's surface would result in voltage variation which can be calculated as demonstrated:
- dW = (δW/δX)dX + (δW/δY)dY + (δW/δZ)dZ = gradW * dx = gdxcos(g,dx)
Transposition (dx) is calculated in the direction of the surface, meaning that dW = 0 or g*dx = 0. This basically means that we're dealing with a pair of vertical vectors and therefore the direction of gravitational pull is always vertical, regardless of location on this surface. The dynamic contact lines are always vertical as well and known as plumb lines or lines of freefall. It is therefore obvious that the vertical direction is always tangent to the plumb lines. Isn't it? The orthometric altitude is then calculated starting from the Geoid's surface and going upwards in the direction of the plumb lines.
Elementary transpositions (dx = dH) in the direction of the plumb lines would result in voltage variation which can be calculated as demonstrated:
- dW = gdHcos(200grad) = - g*dH
This specific formula is rather significant as it actually combines two fundamentally different quantities measured; orthometric altitude and voltage variation. The orthometric altitude is basically a geometric quantity whereas voltage variation is a natural quantity. Due to the fact that the magnitude of gravity (g) differs between different points of such a surface, then it's pretty evident that the value of dH changes accordingly, concerning neighbour surfaces with a constant voltage variation dW. In other words, surfaces of equivalent voltage are not parallel to each other and thus plumb lines are actually spatial lines. Those closed analytical surfaces converge towards the poles outside of the Earth, while they demonstrate inconsistencies regarding their curvature inside the Earth's interior. There's a slight 0,5% decrease of distance between successive surfaces as we move towards the poles. The consistency of the surfaces of equivalent gravitational force is neutralized by the Earth's centrifugal force at a distance of 42 000km from the planet's surface.
Distortion of Spacetime./ Image Source: phys.org
Astronomical Coordinates
In order to define a point's (P) specific position in the 3D world, it's necessary to calculate three different quantities : Φ, Λ, Η (Φ = latitude in degrees, Λ = longtitude in degrees, H = orthometric altitude in meters). A point's dynamic altitude (W) may often be used instead of its orthometric altitude, while there are cases in which the geodynamic number (C) (C = Wo - W = H*g) is the quantity measured and used as the third dimension. The calculation of Φ and Λ defines the vertical direction of a point (P) in relation to the Earth's rotary axis' direction. Observations provide measurements of the values of Φ and Λ which refer to the average rotary axis and are later corrected accordingly by taking into consideration the motion of the planet's poles. The corrected values of Φ and Λ are also known as astronomical latitude and longtitude. Therefore, the quantities measured and corrected (Φ, Λ, Η) / (Φ, Λ, W) / (Φ, Λ, C) are called physical or astronomical coordinates. Mathematical formulas used to transpose astronomical coordinates to cartesian coordinates are extremely complicated and practically inconvenient. As a result, even though astronomical coordinates can be calculated by just utilizing observations, this sort of coordinates is not the appropriate choice to make when establishing geodetic reference systems.
Galactic Coordinate System./ Image Source: star-www.st-and.ac.uk
The measurement and precise calculation of Φ and Λ along with the calculation of the astronomical azimuth (A) through the use of methods developed by the field of geodetic astronomy is becoming rather unpopular in Geodesy. The precise calculation of Φ, Λ and Α was essential in order to accurately determine the position and orientation of the reference ellipsoid in relation to the Geoid. The establishment of precise national reference systems and datums as well as the meticulous and rigid definition of the Geoid were issues of vital importance in those cases. Furthermore, long before satellite and space technology were available, the rigid estimation of Φ and Λ was used for the calculation and definition of the average astronomical plane of Greenwich and the coordinates of the average rotary axis, as well as for the establishment of the global geocentric reference system. The maximum precision demanded while calculating the values of φ and Λ equals one tenth of a second. It's worth noting that the calculation of the value of Λ equals the process of measuring the astral time. Observations utilized in the calculation process of the values of Φ and Λ, along with observation regarding A in cases where it is used, are in fact observations of direction and time in relation to other stars with known galactic coordinates.
Abstentions and variations in orthometric altitude values along with the respective change of geodynamic numbers can be calculated with extreme precision. In most cases precision of more than one hundredth of a meter is achievable through the use of advanced technological instruments, computers and other equipment, and thus demanded. Making sure that surfaces of equivalent altitude are perfectly parallel to each other while creating and defining geodetic datums that serve the purpose of determining altitudes is more than necessary and failing to meet this sort of expectations in unacceptable. Precision can be accomplished by measuring gravity values in the same direction as the plumb lines. It is therefore obvious that points that have the same orthometric height are never situated on the same surface of equivalent altitude. That is the very reason why the use of orthometric heights is much prefered by engineers in cases of practical application.
The Second Equitorial System./ Image Source: star-www.st-and.ac.uk
Hope you made it till this point! That brings us to the end of the third part regarding this Introduction to Geodesy series. In case you have any questions, let me know in the comments below and I will make sure to provide prompt and detailed answers. I've got a lot of stuff to share with you regarding Geodesy and I believe these posts have a great potential to get a lot more advanced as time goes by. Stay tuned and follow at your own risk! ;)

IMAGE SOURCES:
REFERENCES:
University Textbooks and Course Lectures:
Eισαγωγή στη Γεωδαισία /Ιntroduction to Geodesy - TELIONI ELISSAVET (National Technical University of Athens, School of Rural and Surveying Engineering, Course Lecture Notes)
GPS & Γεωδαιτικές Εφαρμογές, Εκδόσεις ΖΗΤΗ / GPS & Geodetic Applications, ZHTH publications. - FWTIOU, PIKRIDAS (National Technical University of Athens, School of Rural and Surveying Engineering, University Textbook)
Δορυφορική Γεωδαισία/ Satellite Geodesy - ΜILAS PARASKEVAS (National Technical University of Athens, School of Rural and Surveying Engineering, Course Lecture Notes)
Aνώτερη Γεωδαισία / Τοp Geodesics - BITHAS ANASTASIOS (National Technical University of Athens, School of Rural & Surveying Engineering, Course Lecture Notes)
Internet Links:


Thank you for your attention!
Hope you did enjoy this post.
Follow me and stay tuned for more engineering blogs.
Highest Regards
@lordneroo
Being A SteemStem Member
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Thanks for the support guys!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
im no bad ass at maths nor calculations. but this is some incredible post right here.
thanks for the insight.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Thanks for reading and leaving a kind comment! ;)
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
good to see a fellow greek being successful. Please keep the quality posts :)
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Thanks for the support and kind words, it's an honor for me!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Hi there @lordneroo, I'm fascinated by your vastness in astronomy. This was evident in the history and theories. Good write up.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Thanks for the kind words!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
@lordneroo i do have a question i have been confused about how the earth gravitational pull is being neutralized by its centrifugal at that distance of about 42000 km force please i will like you to elaborate on that for me thanks
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
@toluakintola0 Hi there, thanks for your question! :)
To be more precise, the Earth's gravitational pull at that distance is balanced by the effect of the centrifugal force induced by its spin. Therefore it would be more accurate to say that the consistency of the surfaces of equivalent gravitational force is neutralized. Keep in mind that the magnitude of gravitational pull depends on distance.
Thanks for pointing that out! I hope you found this comment useful. Let me know if you have any further questions.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
@lordneroo thanks alot for the enlightenment
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
well there is no more to say that thanks for the information!!! I really like it but honestly I don´t like math jajajaj
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
My pleasure, thanks! But why, math is fun :p
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit