
In Book 1 of Euclid’s Elements, Definition 20 reads (Fitzpatrick 6):
| Greek | English |
|---|---|
| κʹ. Τῶν δὲ τριπλεύρων σχημάτων ἰσόπλευρον μὲν τρίγωνόν ἐστι τὸ τὰς τρεῖς ἴσας ἔχον πλευράς, ἰσοσκελὲς δὲ τὸ τὰς δύο μόνας ἴσας ἔχον πλευράς, σκαληνὸν δὲ τὸ τὰς τρεῖς ἀνίσους ἔχον πλευράς. | And of the trilateral figures: an equilateral triangle is that having three equal sides, an isosceles (triangle) that having only two equal sides, and a scalene (triangle) that having three unequal sides. |
In Definition 19, trilaterals were defined as rectilinear figures contained by three straight lines. Definition 20 simply establishes the correct terminology to be used when describing three particular types of trilaterals. These three types are each defined in terms of the relative lengths of their sides:
If all three sides are of the same length, then the trilateral is an equilateral triangle.
If two and only two sides are of equal length, then the trilateral is an isosceles triangle.
If all three sides are of different lengths, then the trilateral is a scalene triangle.
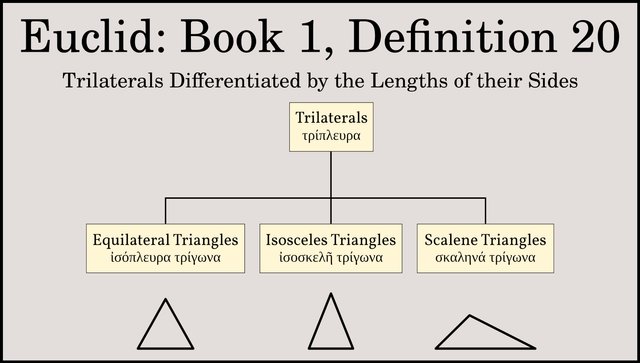
Note that Euclid does not consider an equilateral triangle to be also an isosceles triangle. He specifies that an isosceles triangle must have only two [δύο μόνας] equal sides. Modern geometricians prefer to define an isosceles triangle as one in which at least two sides are of equal length, a definition that includes equilateral triangles. Nevertheless, when Euclid uses the term isosceles triangle elsewhere in the Elements, what he says always covers equilateral triangles as well. For example, Proposition 1:5 states that the angles at the base of an isosceles triangle are equal to one another—which is also true of equilateral triangles.
Note also that Euclid uses the common term for triangle [τρίγωνόν] in addition to his more technical term trilateral [τρίπλευρον]. As we saw in the last article, he only uses the term trilateral in Definitions 19 and 20. Thereafter, he always refers to trilaterals as triangles.
The technical terms isosceles and scalene were already in common use before Euclid commandeered them. As Heath points out, Plato and Aristotle used the former in the Euclidean sense (Timaeus 54 a ff, Cooper 1256 ff : Prior Analytics 41 b, Barnes 159). Aristotle also used the latter in the Euclidean sense (Posterior Analytics 74 a, Barnes 276). In his dialogue Euthyphro, Plato applied the terms isosceles and scalene to even and odd numbers respectively (Euthyphro 12 d, Cooper 12).
In his Treatise on Conic Sections, Apollonius of Perga used the term scalene to describe an oblique circular cone—ie a cone with a circular base, but in which the axis passes through the centre of the base non-perpendicularly (Heath 187-188). Apollonius flourished about a century after Euclid.
The etymology of the Greek term σκαληνός, scalene, is uncertain, which perhaps accounts for the different uses to which it was applied.

Modern Editions
In his 1814 edition of the Elements, François Peyrard divided this definition into three separate definitions, numbered 24, 25 and 26 (Peyrard 3-4). Ernst Ferdinand August, in his edition of 1826, followed suit (August 2). In 1883, Johan Ludvig Heiberg re-integrated these into a single definition, numbered 20 (Heiberg 6-7). This is believed to correspond to Euclid’s original manuscript. In his apparatus criticus, Heiberg noted:
Def. 20 is commonly divided into 3. (Heiberg 7)
One curious discrepancy between August’s edition and the other two involves the word only in the definition of an isosceles triangle. August uses the adverb μόνον [monon], whereas the other two editors use the adjective μόνας [monas] (feminine accusative plural to agree with πλευράς, sides). As Heiberg notes in his apparatus criticus, Proclus used the adverbial form, so this is an old variant (Heiberg 7, Morrow 130).
And that’s a good place to stop.
References
- Ernst Ferdinand August, Euclidis Elementa, Part 1, Theodor Trautwein, Berlin (1826)
- Jonathan Barnes (editor), The Complete Works of Aristotle, Volumes 1 & 2, Princeton University Press, Princeton, NJ (1984)
- John M Cooper, Plato: Complete Works, Hackett Publishing Company, Indianapolis (1997)
- Richard Fitzpatrick (translator), Euclid’s Elements of Geometry, University of Texas at Austin, Austin, TX (2008)
- Thomas Little Heath (translator & editor), The Thirteen Books of Euclid’s Elements, Second Edition, Dover Publications, New York (1956)
- Johan Ludvig Heiberg, Heinrich Menge, Euclidis Elementa edidit et Latine interpretatus est I. L. Heiberg, Volumes 1-5, B G Teubner Verlag, Leipzig (1883-1888)
- Henry George Liddell, Robert Scott, A Greek-English Lexicon, Eighth Edition, American Book Company, New York (1901)
- Glenn Raymond Morrow (translator), Proclus: A Commentary on the First Book of Euclid’s Elements, Princeton University Press, Princeton, NJ (1970)
- François Peyrard, Les Œuvres d’Euclide, en Grec, en Latin et en Français, Volumes 1-3, Revised Edition, Charles-Frobert Patris, Paris (1814, 1816, 1818)
Online Resources
