
In Book 1 of Euclid’s Elements, Postulate 2 reads (Fitzpatrick 7):
| Greek | English |
|---|---|
| βʹ. Καὶ πεπερασμένην εὐθεῖαν κατὰ τὸ συνεχὲς ἐπ εὐθείας ἐκβαλεῖν. | 2. And to produce a finite straight-line continuously in a straight-line. |
As we saw in the last article, the verb Ἠιτήσθω [Ēitēsthō], Let it have been postulated, is understood to apply to all five postulates.
In some early manuscripts, the order of the words is slightly different:
Καὶ πεπερασμένην εὐθεῖαν ἐπ εὐθείας κατὰ τὸ συνεχὲς ἐκβαλεῖν. (Heiberg 8-9)
Heiberg notes that V [a Viennese MS of the 11-12th century], Proclus, Simplicius, Capella, Boethius, and Campanus maintain the received order. Among modern editions of the Elements, only François Peyrard’s Paris edition of 1814-1818 has the alternative word-order (Peyrard 5). In Peyrard’s critical notes, though, he acknowledges that the received order can be found in several manuscripts (Peyrard 454).
Euclid’s πεπερασμένην εὐθεῖαν, finite straight line, refers to what we today would call a line-segment:
I translate πεπερασμένην by finite, because that is the received equivalent, and because any alternative word such as limited, terminated, if applied to a straight line, would equally fail to express what modem Italian geometers aptly call a rectilineal segment, that is, a straight line having two extremities. (Heath 196)

The verb ἐκβαλεῖν [ekbalein], to produce (a line)—meaning to extend or lengthen a line—had been used in this technical sense by Aristotle (Liddell & Scott 430):
Εἰ γὰρ ἄπειρον τὸ κύκλῳ φερόμενον σῶμα, ἄπειροι ἔσονται αἱ ἀπὸ τοῦ μέσου ἐκβαλλόμεναι.
[For if the body being carried in a circle is infinite, those [radii] which are produced from the middle [ie the centre of the circle] will be infinite.] (On the Heavens 1:5, Aristotle 271b29-30, Barnes 452)
Finite or Infinite
This postulate is somewhat ambiguous. Does Euclid mean that given a finite line-segment, one can extend it indefinitely in both directions to create an infinitely long line? Modern geometry does not have a problem with defining a line as an infinitely long object without width or depth, but did Euclid regard such a thing as possible?
Here we have the second ability of a straightedge, namely, to extend a given line AB to CD. This postulate does not say how far a line can be extended. Sometimes it is used so that the extension equals some other line. Other times it is extended arbitrarily far. (Joyce)
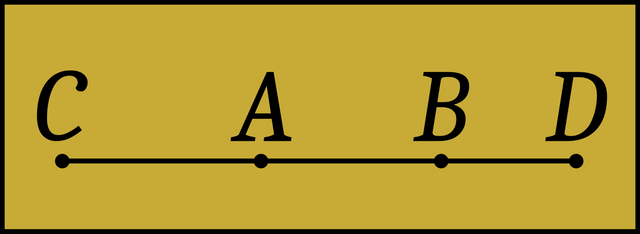
The phrase κατὰ τὸ συνεχὲς [kata to sunekhes] means continuously, but Proclus understands this to include indefinitely:
But we must understand that the character of being produced indefinitely does not belong to all lines [ie it only belongs to straight lines] ... (Morrow 147)
Does Proclus’ indefinitely include infinitely?
In his 1792 edition of Proclus, the English Neoplatonist Thomas Taylor translated Euclid’s Postulate 2 thus:
That a terminated straight line may be produced to any length in a straight line. (Taylor 2:6)
And Taylor’s translation of the passage we just quoted from Proclus explicitly implies that Postulate 2 allows for the infinite extension of a line-segment:
But it is requisite to know, that every line cannot be infinitely produced ... (Taylor 2:8)
Henry Billingsley, who published the first English translation of the Elements in 1570, also understood this postulate to include the infinite extension of a finite line-segment:
As to draw in length continually the right line AB, who will not graunt? For there is no magnitude so great, but that there maybe a greter, nor any so litle but that there may be a lesse. And a line is a draught from one point to an other, therfore from the point B, which is the ende of the line AB, may be drawn a line to some other point, as to the point C, and from that to an other, and so infinitely. (Billingsley Folio 6)

Uniqueness
As in Postulate 1, Euclid does not state explicitly that the straight line which results when this Postulate is applied to a finite line-segment is unique. It could be argued that as this Postulate allows for a finite line-segment to be extended in one or the other direction—or in both directions—by any arbitrary amount, it allows for the generation of any number of new line-segments, and not a unique one. Nevertheless, Euclidean geometry requires that if two straight infinite lines share a common line-segment, then they must be one and the same line:
Just as Post. 1 asserting the possibility of drawing a straight line from any one point to another must be held to declare at the same time that the straight line so drawn is unique, so Post. 2 maintaining the possibility of producing a finite straight line (a “rectilineal segment”) continuously in a straight line must also be held to assert that the straight line can only be produced in one way at either end, or that the produced part in either direction is unique; in other words, that two straight lines cannot have a common segment ... (Heath 196)
Although Euclid does not include this fact in any of his postulates, he does make use of it in Proposition 11:1, the first proposition that deals with solid (three-dimensional) geometry:
As with the first postulate, it is implicitly assumed in the books on plane geometry that when a line is extended, it remains in the plane of discussion. The first proposition on solid geometry, proposition XI.1, claims that a line can’t be only partly in a plane. The central step in the proof of that proposition is to show that a line cannot be extended in two ways, that is, there is only one continuation of a line. The proof is hardly convincing. Rather, this postulate should include a clause to that effect. (Joyce)
Richard Fitzpatrick, whose translation of the Elements I am following, is even more damning of Euclid:
The proofs of the first three propositions in this book [ie Book 11] are not at all rigorous. Hence, these three propositions should properly be regarded as additional axioms. (Fitzpatrick 426)
He also finds the proof of 11:1 circular. Euclid’s proof hinges on a particular assumption:
This assumption essentially presupposes the validity of the proposition under discussion. (Fitzpatrick 426)
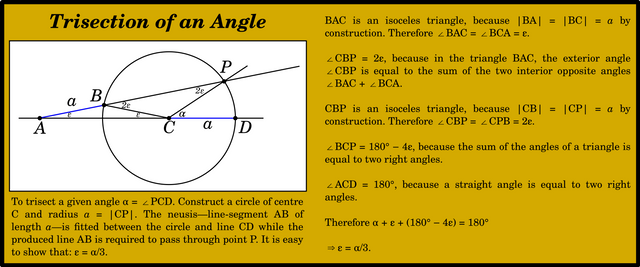
Neusis
Another subject discussed by David Joyce in relation to this postulate is a form of geometric construction known as neusis:
A neusis is a geometrical construction, in which a straight line of given length has to be placed between two other given lines in such a way that its continuation verges (Greek verb neuein) toward a given point. (Sefrin-Weis xvii fn 1)
The Greek geometers introduced this type of construction when they discovered that the trisection of a plane angle could not be carried out using only a straightedge and a compass:
The Trisection of any Angle. This problem presumably arose from attempts to continue the construction of regular polygons after that of the pentagon had been discovered. The trisection of an angle would be necessary in order to construct a regular polygon the sides of which are nine, or any multiple of nine, in number. A regular polygon of seven sides, on the other hand, would no doubt be constructed with the help of the first discovered method of dividing any angle in a given ratio, i.e. by means of the quadratrix. This method covered the case of trisection, but other more practicable ways of effecting this particular construction were in due time evolved.
We are told that the ancients attempted, and failed, to solve the problem by ‛plane’ methods, i.e. by means of the straight line and circle; they failed because the problem is not ‛plane’ but ‛solid’. Moreover, they were not yet familiar with conic sections, and so were at a loss; afterwards, however, they succeeded in trisecting an angle by means of conic sections, a method to which they were led by the reduction of the problem to another, of the kind known as νεῦσεις (inclinationes, or vergings) [Footnote: Pappus iv, p. 272. 7-14] (Heath 1921:238 : Sefrin-Weis 146)
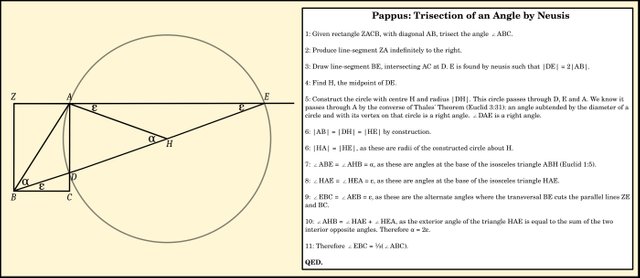
Everything in Pappus’s construction (Pappus 4:32, Ver Eecke 212, Hultsch 274-277) can be carried out using a straightedge and a compass except for the positioning of the point E. In practice, E is moved continuously along the line ZA until the sweet spot is found where |DE| = 2|AB|. This can only be achieved using a marked ruler or other measured device. The inclination (Greek: νεῦσις) of BE is adjusted to satisfy this requirement.
Euclid has no postulate for neusis constructions, and since neusis constructions can trisect angles, we conclude from Wantzel’s theorem that another postulate is required to justify neusis constructions. (Joyce)
All constructions in Euclidean geometry can be carried out using only a compass and a straightedge. But the trisection of plane angles requires a neusis construction. The fact that Euclid does not include the trisection of angles in the Elements is a strong indicator that he rejected the validity of this type of construction.
The simplest explanation of this, however, is that Euclid’s geometry is not constructive in any sense of the word : it is Platonic. Euclid’s geometric objects are not material things that one can construct by some means or other—whether with a compass and a straightedge or by neusis. They are perfect, eternal Platonic Forms that have always existed. If they were ever constructed, they were constructed by the Demiurge, the divine architect who shaped our World.
And that’s a good place to stop.
References
- Ernst Ferdinand August, Euclidis Elementa, Part 1, Theodor Trautwein, Berlin (1826)
- Jonathan Barnes (editor), The Complete Works of Aristotle: The Revised Oxford Translation, Volume 1, Princeton University Press, Princeton, NJ (1984)
- Henry Billingsley (translator), The Elements of Geometrie of the Most Auncient Philosopher Evclide of Megara, John Day, London (1582)
- Richard Fitzpatrick (translator), Euclid’s Elements of Geometry, University of Texas at Austin, Austin, TX (2008)
- Thomas Little Heath, A History of Greek Mathematics, Volume 1: From Thales to Euclid, The Clarendon Press, Oxford (1921)
- Thomas Little Heath (translator & editor), The Thirteen Books of Euclid’s Elements, Second Edition, Dover Publications, New York (1956)
- Johan Ludvig Heiberg, Heinrich Menge, Euclidis Elementa edidit et Latine interpretatus est I. L. Heiberg, Volumes 1-5, B G Teubner Verlag, Leipzig (1883-1888)
- Friedrich Otto Hultsch (translator & editor), Pappi Alexandrini Collectionis Quae Supersunt, Volume 1, Weidmannsche Buchhandlung, Berlin (1877)
- Henry George Liddell, Robert Scott, A Greek-English Lexicon, Eighth Edition, American Book Company, New York (1901)
- Glenn Raymond Morrow (translator), Proclus: A Commentary on the First Book of Euclid’s Elements, Princeton University Press, Princeton, NJ (1970)
- François Peyrard, Les Œuvres d’Euclide, en Grec, en Latin et en Français, Volumes 1-3, Charles-Frobert Patris, Paris (1814, 1816, 1818)
- Heike Sefrin-Weis, Pappus of Alexandria: Book 4 of the Collection, Springer, London (2010)
- Thomas Taylor, The Philosophical and Mathematical Commentaries of Proclus on the First Book of Euclid’s Elements, Volume 1, Volume 2, London (1792)
- Paul Ver Eecke (translator & editor), Pappus D’Alexandrie: La Collection Mathématique, Volume 1, Desclée de Brouwer et Cie, Paris (1933)
Image Credits
- Thomas Little Heath: Anonymous Photograph, Public Domain
- Euclid: The Thirteen Books of the Elements: Paul E Kennedy (cover designer), © Dover Publications, Fair Use
Online Resources
