In Book 1 of Euclid’s Elements, Postulate 5 reads (Fitzpatrick 7):
| Greek | English |
|---|---|
| εʹ. Καὶ ἐὰν εἰς δύο εὐθείας εὐθεῖα ἐμπίπτουσα τὰς ἐντὸς καὶ ἐπὶ τὰ αὐτὰ μέρη γωνίας δύο ὀρθῶν ἐλάσσονας ποιῇ, ἐκβαλλομένας τὰς δύο εὐθείας ἐπ ̓ ἄπειρον συμπίπτειν, ἐφ ̓ ἃ μέρη εἰσὶν αἱ τῶν δύο ὀρθῶν ἐλάσσονες. | 5. And that if a straight-line falling across two (other) straight-lines makes internal angles on the same side (of itself whose sum is) less than two right-angles, then the two (other) straight-lines, being produced to infinity, meet on that side (of the original straight-line) that the (sum of the internal angles) is less than two right-angles (and do not meet on the other side). |
As we saw in a previous article, the verb Ἠιτήσθω [Ēitēsthō], Let it have been postulated, is understood to apply to all five postulates.
Some manuscripts add the word γωνίαι [gōnia], angles after ἐλάσσονες [elassones], less. Among modern editions of the Elements, only François Peyrard’s 1814 edition includes this additional word (Peyrard 5, 454). Peyrard also includes the word τις [tis], any, after εὐθεῖα [eutheia], straight line.
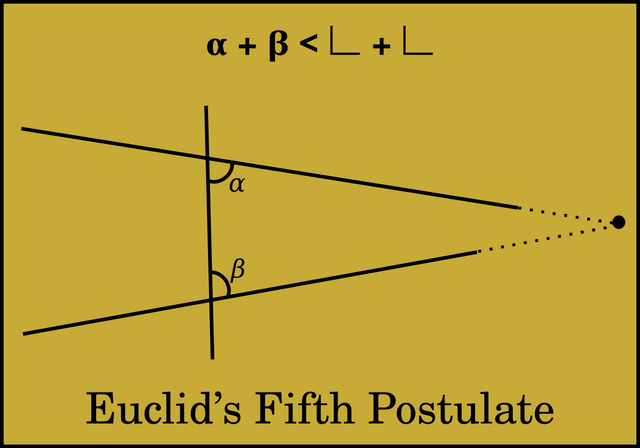
This cumbersome postulate is sometimes expressed in an alternative and simpler form, which can be shown to have the same meaning:
Given a straight line in a plane and a point in the same plane that is not on the given line, there is one and only one straight line in the plane that is parallel to the given line.
This is Playfair’s Axiom, which was postulated by the Scottish mathematician John Playfair in his Elements of Geometry in 1795. Playfair makes it the last of his eleven axioms:
Two straight lines cannot be drawn through the same point, parallel to the same straight line, without coinciding with one another. (Playfair 7)
Euclid’s Fifth Postulate is probably the most famous and controversial thing in the Elements. More ink has been spilt expounding these few lines than on the rest of the Elements put together. Over the centuries countless mathematicians have tried to prove this postulate using only the first four postulates and the five common notions as axioms. Several have even claimed to have succeeded. But when these “proofs” are examined with the fine-tooth comb of the logician, they are always found to contain an assumption that is equivalent to the Fifth Postulate or that requires the Fifth Postulate for its own proof.

There is no more striking evidence of Euclid’s genius than his realization that his notorious fifth postulate was not a theorem but an axiom that had to be accepted without proof. (Gardner 175)
While conceding Euclid’s genius in this regard, some commentators have nevertheless emended his Fifth Postulate to make it quite watertight:
Of course, this is a postulate for plane geometry. It should include the condition that the two straight lines lie in a plane, otherwise, skew lines in space would satisfy the hypotheses. Also, without an ambient plane, the term “that side [of the straight line]” has no meaning. (Joyce)
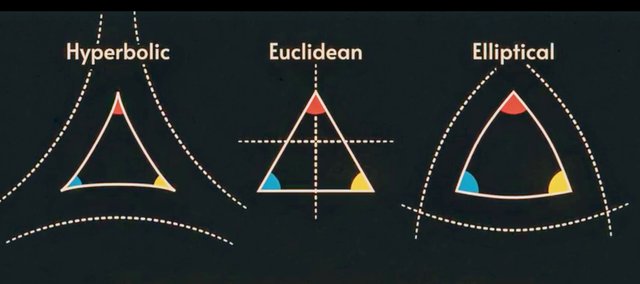
Denying the Fifth Postulate leads to non-Euclidean geometries. At first, these were thought to be absurd—surely there was only one true geometry, the geometry which described the real world? But in the 19th century mathematicians finally came to recognize that non-Euclidean geometries were just as valid as Euclidean geometry. It was even suspected by some physicists that the real world might not be Euclidean after all.

The parallel postulate is historically the most interesting postulate. Geometers throughout the ages have tried to show that it could be proved from the remaining postulates so that it wasn’t necessary to assume it. The process tried was to assume its falsehood, then derive a contradiction. Many strange conclusions follow from denying the parallel postulate, and several geometers found such great absurdities that they concluded that the parallel postulate did follow from the rest.
Nevertheless, these apparent absurdities are not contradictions. In the early nineteenth century, Bolyai, Lobachevsky, and Gauss found ways of dealing with this non-Euclidean geometry by means of analysis and accepted it as a valid kind of geometry, although very different from Euclidean geometry. This hyperbolic geometry, as it is called, is just as consistent as Euclidean geometry and has many uses.
Thus, we know now that we must include the parallel postulate to derive Euclidean geometry. (Joyce)
As we saw in the last article, these 19th-century mathematicians were actually anticipated by the Italian geometrician Giovanni Girolamo Saccheri:
As early as 1733, in a Latin book called Euclid Cleared of All Blemish, Saccheri actually constructed both types of non-Euclidean geometry [hyperbolic and elliptic] ... without knowing it! Or so it seems. At any rate Saccheri refused to believe either geometry was consistent, but he came so close to accepting them that some historians think he pretended to disbelieve them just to get his book published, (Gardner 177)

In hyperbolic geometry an infinite number of parallel lines pass through the point-not-on-the-given-line, while in elliptic geometry no parallel line passes through it.
One of the great ironies in the history of geometry is that spherical geometry, which Euclid and his contemporaries studied in great detail, is actually a non-Euclidean geometry. Spherical geometry is a special case of elliptic geometry—just as a circle is a special type of ellipse, and a sphere a special type of ellipsoid. The ancient geometers, however, always studied the sphere as a two-dimensional surface existing in a three-dimensional Euclidean space, so they never recognized it as a separate geometry in its own right. If, however, we restrict ourselves entirely to the two-dimensional surface of the sphere, then it becomes clear that the fundamental principles underpinning this geometry are quite different from Euclid’s Five Postulates. In spherical geometry, for example, the role of straight lines is taken by great circles, which requires the postulate: There are no parallel lines in spherical geometry—which is the defining property of elliptic geometries.
It is the Fifth Postulate which distinguishes Euclidean geometry from non-Euclidean geometries. As Euclid’s translator Richard Fitzpatrick puts it:
This postulate effectively specifies that we are dealing with the geometry of flat, rather than curved, space. (Fitzpatrick 7)
Parallel Postulate
The Fifth Postulate is often referred to as the Parallel Postulate. Euclid defined parallelism in Definition 23 of Book 1:
Parallel lines are straight-lines which, being in the same plane, and being produced to infinity in each direction, meet with one another in neither (of these directions). (Fitzpatrick 7)
In his Prior Analytics, Aristotle pointed out that contemporary geometricians were guilty of the logical fallacy known as begging the question, or petitio principii, when they attempted to construct parallel lines:
Now some things are naturally knowable through themselves, and others through something else ... and when anyone tries to prove by means of itself that which is not knowable by means of itself, then he is begging the point at issue. This may be done by directly postulating the proposition which is to be proved; but we may also have recourse to some other propositions of a sort which are of their very nature proved by means of our proposition, and prove the point at issue by means of them: e.g., supposing that A is proved by B and B by C, and it is the nature of C to be proved by A; for if anyone argues in this way it follows that he is proving A by means of itself. This is exactly what those persons do who think that they are drawing parallel lines; for they do not realize that they are making assumptions which cannot be proved unless the parallel lines exist. (Tredennick 485-487, Prior Analytics 2:16)

Euclid circumvented all such criticisms by stating the Parallel Postulate at the very outset of the Elements:
When we consider the countless successive attempts made through more than twenty centuries to prove the Postulate, many of them by geometers of ability, we cannot but admire the genius of the man who concluded that such a hypothesis, which he found necessary to the validity of his whole system of geometry, was really indemonstrable. (Heath 202)
Euclid’s translator Thomas Little Heath devotes nineteen pages to the Fifth Postulate. Sixteen of these relate to the history of this Postulate as it applies to Ptolemy, Proclus, Nasir al-Din al-Tusi, John Wallis, Saccheri, Johann Heinrich Lambert, and Adrien-Marie Legendre. Interesting though all this is, it is not particularly relevant to a study of the Elements. For the most part Heath examines several spurious “proofs” of the Parallel Postulate and exposes their flaws. No less than six pages are devoted to Legendre, who spent forty years of his life in quest of the elusive proof.

Heath concludes his discussion with a list of no less than eleven alternative ways of expressing Euclid’s Parallel Postulate:
Through a given point only one parallel can be drawn to a given straight line or, Two straight lines which intersect one another cannot both be parallel to one and the same straight line. This is commonly known as “Playfair’s Axiom,” but it was of course not a new discovery. It is distinctly stated in Proclus’ note to Euclid 1:31.
If a straight line intersect one of two parallels, it will intersect the other also (Proclus).
Straight lines parallel to the same straight line are parallel to one another.
There exist straight lines [that are] everywhere equidistant from one another (Posidonius and Geminus); with which may be compared Proclus’ tacit assumption that Parallels remain, throughout their length, at a finite distance from one another.
There exists a triangle in which the sum of the three angles is equal to two right angles (Legendre).
Given any figure, there exists a figure similar to it of any size we please (Wallis, Carnot, Laplace). Saccheri points out that it is not necessary to assume so much, and that it is enough to postulate that there exist two unequal triangles with equal angles.
Through any point within an angle less than two-thirds of a right angle a straight line can always be drawn which meets both sides of the angle (Legendre). With this may be compared the similar axiom of Lorenz (Grundriß der reinen und angewandten Mathematik oder erster Cursus der gesamten Mathematik, 1791): Every straight line through a point within an angle must meet one of the sides of the angle.
Given any three points not in a straight line, there exists a circle passing through them (Legendre, Bolyai).
“If I could prove that a rectilineal triangle is possible the content of which is greater than any given area, I am in a position to prove perfectly rigorously the whole of geometry” (Gauss, in a letter to Bolyai, 1799). Cf ... the axiom of Worpitzky: There exists no triangle in which every angle is as small as we please.
If in a quadrilateral three angles are right angles, the fourth angle is a right angle also (Clairaut, 1741).
If two straight lines are parallel, they are figures opposite to (or the reflex of) one another with respect to the middle points of all their transversal segments (Veronese, Elements, 1904). Or: Two parallel straight lines intercept, on every transversal which passes through the middle point of a segment included between them, another segment the middle point of which is the middle point of the first (Ingrami, Elementi, 1904).
And that’s a good place to stop.
References
- Ernst Ferdinand August, Euclidis Elementa, Part 1, Theodor Trautwein, Berlin (1826)
- Henry Billingsley (translator), The Elements of Geometrie of the Most Auncient Philosopher Evclide of Megara, John Day, London (1582)
- Richard Fitzpatrick (translator), Euclid’s Elements of Geometry, University of Texas at Austin, Austin, TX (2008)
- Martin Gardner, The Colossal Book of Mathematics: Classic Puzzles, Paradoxes, and Problems, W W Norton & Company, New York (2001)
- George Bruce Halsted (editor & translator), Girolamo Saccheri’s Euclides Vindicatus, The Open Court Publishing Company, Chicago (1920)
- Thomas Little Heath (translator & editor), The Thirteen Books of Euclid’s Elements, Second Edition, Dover Publications, New York (1956)
- Johan Ludvig Heiberg, Heinrich Menge, Euclidis Elementa edidit et Latine interpretatus est I. L. Heiberg, Volumes 1-5, B G Teubner Verlag, Leipzig (1883-1888)
- Henry George Liddell, Robert Scott, A Greek-English Lexicon, Eighth Edition, American Book Company, New York (1901)
- Glenn Raymond Morrow (translator), Proclus: A Commentary on the First Book of Euclid’s Elements, Princeton University Press, Princeton, NJ (1970)
- François Peyrard, Les Œuvres d’Euclide, en Grec, en Latin et en Français, Volumes 1-3, Charles-Frobert Patris, Paris (1814, 1816, 1818)
- John Playfair, Elements of Geometry, Bell & Bradfute, Edinburgh (1795)
- Thomas Taylor, The Philosophical and Mathematical Commentaries of Proclus on the First Book of Euclid’s Elements, Volume 1, Volume 2, London (1792)
- Hugh Tredennick (translator), Aristotle: Prior Analytics, Loeb Classical Library, Harvard University Press, Cambridge, Massachusetts (1967)
Image Credits
- John Playfair: Henry Raeburn (artist), National Portrait Gallery, London, Public Domain
- János Bolyai: Ferenc Márkos (artist), Creative Commons License
- Nikolai Lobachevsky: Lev Kriukov (artist), Lev Tolstoy Museum, Moscow, Public Domain
- Carl Friedrich Gauss: Christian Albrecht Jensen (artist), The Pushkin State Museum of Fine Arts, Moscow, Public Domain
- Via Padre Girolamo Saccheri (Sanremo, Italy): Anonymous Photograph, Copyright Unknown, Fair Use
- Euclidean, Hyperbolic and Elliptic Geometries: © The Book of Threes, Fair Use
- Aristotle: Roman Copy of a Greek Bronze Original by Lysippos (330 BCE), Museo Nazionale Romano di Palazzo Altemps, Rome, Jastrow (photographer), Public Domain
- Adrien-Marie Legendre: René de Lenclos (artist), Creative Commons License
Online Resources
